
Để giúp các em học sinh chuẩn bị tốt cho kỳ thi tuyển sinh vào lớp 6 Trường THCS THPT Lương Thế Vinh, MATHX biên soạn đến các em giải chi tiết đề thi tuyển sinh vào 6 môn Toán THCS Lương Thế Vinh 2013-2014. Hy vọng rằng tài liệu giải chi tiết này sẽ là công cụ hữu ích, giúp các em nắm bắt được cấu trúc của đề thi, rèn luyện kỹ năng giải bài một cách linh hoạt và chủ động. Chúc các em học sinh có những kết quả xuất sắc trong kỳ thi sắp tới và đạt được vé vào cổng trường mong muốn.
Phụ huynh và các em học sinh xem thêm danh sách đáp án và lời giải chi tiết đề thi vào 6 trường THCS và THPT Lương Thế Vinh các năm tại đây:
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2004 - 2005
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2005 - 2006
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2006 - 2007
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2007 - 2008
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2010 - 2011
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2011 - 2012
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2012 - 2013
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2013 - 2014
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2014 - 2015
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2018 - 2019
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2019 - 2020
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2020 - 2021
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2021 - 2022
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2022 - 2023
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2023 - 2024
Các em học sinh tải đề về luyện tập làm trước khi đối soát với đáp án bên dưới:
Môn: Toán
Năm học: 2013 - 2014
Bài 1: Số nào tiếp theo 5 số sau đây: 1; 3; 6; 10; 15 ; …?
Hướng dẫn:
1 + 2 = 3
3 + 3 = 6;
6 + 4 = 10;
10 + 5 = 15;
15 + 6 = 21; 21 + 7 = 28; 28 + 8 = 36; 36 + 9 = 45; 45 + 10 = 55
Đáp số: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55
Bài 2: Một người mang trứng đi bán. Lần thứ nhất ông ta bán được một nửa số trứng và nửa quả trứng (không phải đập quả trứng nào cả). Lần thứ hai ông bán nửa số trứng còn lại và nửa quả trứng. Các lần bán tiếp theo cũng như vậy, nghĩa là bán được nửa số trứng còn lại và nủa quả trứng. Sau lần bán thứ 5 chỉ còn lại 1 quả trứng. Hỏi lúc chưa bán ông có bao nhiêu quả trứng?
Hướng dẫn:
Lần 1 bán: \(\dfrac {1}{2}\) x số trứng + 0,5
Lần 2 bán được: \(\dfrac {1}{4}\) x số trứng + 0,5
.....
Lần thứ 5 bán được: \(\dfrac {1}{2×2×2×2×2}\)X số trứng + 0,5 = \(\dfrac {1}{32}\) x số trứng + 0,5
Số trứng còn lại sau lần bán thứ 5 là:
Số trứng - (bán lần 1 + bán lần 2 +... + bán lần 5) = 1
Số trứng - [(\(\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{8} + \dfrac{1}{{16}} + \dfrac{1}{{32}}\ \)) x số trứng + 0,5 x5] = 1
Số trứng - \(\dfrac {16+8+4+2+1}{32}\) x số trứng - 2,5 = 1
Số trứng - \(\dfrac {31}{32}\)x số trứng = 3,5
\(\dfrac {1}{32}\) x số trứng = 3,5
Số trứng = 3,5 x 32 = 112 (quả)
Đáp số: 112 quả trứng.
Bài 3: Tổng các số tự nhiên từ 50 đến 100 bằng bao nhiêu?
Hướng dẫn:
SSH = \((100-50):1+1=51\) (số)
Tổng = \((50+100)\times51:2=3825\)
Đáp số: 3825
Bài 4: Cho phân số \(\dfrac {45}{53}\). Tìm số tự nhiên a sao cho nếu cộng vào mẫu số của phân số đã cho a đơn vị và giữ nguyên tử số ta được phân số mới bằng \(\dfrac {3}{4}\)?
Hướng dẫn:
Phân số ban đầu: \(\dfrac {45}{53}\)
Phân số sau khi thêm a vào mẫu: \(\dfrac {45}{53+a}\)
Theo để bài cho thì: \(\dfrac {45}{53+a}\) = \(\dfrac {3}{4}\)
Tương tự bài các đề trước, 2 phân số bằng nhau khi tích chéo của chúng bằng nhau:
45 x 4 = 3 x (53 + a)
180 = 159 + 3 xa
180 - 159 = 3 x a
a = 21 : 3 = 7
Đáp số: 7.
Bài 5: Tìm hai số tự nhiên có tích bằng 10.000 biết rằng các chữ số của hai số đó đều khác 0?
Hướng dẫn:
Tích của 10.000 có 4 chữ số 0 ở cuối. Vậy các số trong tích phải tích tích được thành tích của ít nhất là 4 số 5 và 4 số chẵn.
Trường hợp đơn giản nhất lấy số chẵn là 2.
5 x 5 x 5 x 5 x 2 x 2 x 2 x 2 x a = 10.000
a x 10.000 = 10.000
a = 1.
Vì 2 số cần tìm có các chữ số phải khác không nên:
Số thứ nhất là: 5 x 5 x 5 x 5 = 625.
Số thứ hai là: 2 x 2 x 2 x 2 = 16.
Đáp số: 625 và 16.
Bài 6: Người ta trộn 3 tấn quặng 45% sắt với 7 tấn quặng chứa 55% sắt. Hỏi hỗn hợp chứa bao nhiêu % sắt?
Hướng dẫn:
Số sắt có trong số quặng thứ nhất là: 45% x 3 = I,35 tấn
Số sắt có trong số quặng thứ hai là: 55% x 7= 3,85 (tấn)
Tổng số sắt có trong hỗn hợp quặng là: 1,35 + 3,85 = 5,2 (tấn)
Tổng số quặng là: 3 + 7 = 10 (tấn)
Số % sắt có trong hỗn hợp quặng là: 5,2 : 10 x 100 (%) = 52 (%)
Đáp số: 52 %
Bài 7: Năm nay số tuổi của bố gấp 6 lần số tuổi của con, Sau 20 năm nữa thì số tuổi của bố gấp 2 lần số tuổi của con. Hỏi năm nay bố bao nhiêu tuổi và con bao nhiêu tuổi?
Hướng dẫn:
Gọi số tuổi hiện tại của con là a (tuổi) thì số tuổi của bố hiện tại là 6 x a (tuổi)
Sau 20 năm: số tuổi của con là a + 20 (tuổi) và của bố là 6 x a + 20 (tuổi)
Vì sau 20 năm, tuổi bố gấp 2 lần tuổi con nên:
6 x a + 20 = 2 x (a + 20)
6 x a + 20 = 2 x a + 40
6 x a - 2 x a = 40 - 20
4 x a = 20
a = 20 : 4 = 5
Vậy hiện tại con 5 tuổi và bố là 5 x 6 = 30 tuổi
Đáp số: Con 5 tuổi và bố 30 tuổi.
Bài 8: Trong các hình chữ nhật có chu vi bằng 20m, hình có diện tích lớn nhất bằng bao nhiêu?
Hướng dẫn:
Trong các hình chữ nhật có cùng chu vi, hình vuông là hình có diện tích lớn nhất.
Chú ý là hình vuông cũng là hình chữ nhật nhưng đặc biệt hơn là có các cạnh bằng nhau.
Chu vi hình vuông là: 20 (m)
Cạnh của hình vuông sẽ là: 20 : 4= 5 (m),
Diện tích sẽ là: 5 x 5 = 25 (\({{m^2}}\))
Đáp số: 25 \({{m^2}}\)
Bài 9: Một sàn nhà hình chữ nhật có chiều dài 7,2m và chiều rộng 5,1m được lát bằng các viên gạch hoa hình vuông có cạnh là 3 dm. Hỏi phải cần bao nhiêu viên gạch hoa để lát kín sàn nhà?
Hướng dẫn:
Diện tích sàn nhà : diện tích 1 viên gạch lát = số gạch cần lát
Vậy cần phải đi tìm diện tích sản nhà và diện tích 1 viên gạch
Diện tích của sản nhà là: 7,2 x 5,1 = 36,72 (\({{m^2}}\))
Diện tích của một viên gạch hoa là: 3 x 3 = 9 (\({{dm^2}}\)) = 0,09 (\({{m^2}}\))
Số gạch cần đề lát sàn nhà là: 36,72 : 0,09 = 408 (viên gạch)
Chú ý rằng trong thực tế các viên gạch không thể lắp sít vào nhau như vậy được.
Đáp số: 408 viên gạch.
Bài 10: Một vòi nước chảy vào bể, cứ 20 phút 30 giây thì chảy được 5 \({{m^3}}\) nước. Biết thể tích bể là 11 \({{m^3}}\). Hỏi để chảy đầy bể thì cần bao nhiêu thời gian?
Hướng dẫn:
Đổi 20 phút 30 giây = 20,5 phút
Thời gian đề vòi chảy được 1 \({{m^3}}\) bể là
20,5: 5 = 4,1 (phút)
Thời gian đề vòi chảy được 11 \({{m^3}}\) bẻ là
4,1 x 11 = 45,1 phút = 45 phút 6 giây
Đáp số: 45 phút 6 giây.
Bài 11: Mười người gặp nhau trong một cuộc họp, hai người nào cũng bắt tay nhau một lần. Hỏi có bao nhiêu cái bắt tay?
Hướng dẫn:
Số lượt bắt tay sẽ là:
9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45 (chiếc bắt tay)
Hướng dẫn lại chút:
Ban đầu có 10 người, nếu 1 người bắt tay tất cả mọi người rồi đi về thì có tất cả 9 cái bắt tay, vậy người này đã bắt tay với hết tắt cả mọi người.
Sau đó còn 9 người, lại có 1 người nữa bắt tay với tất cả mọi người đề đi về thì số bắt tay sẽ là 8 cái.
.....
Chỉ còn lại 2 người, thì 2 người bắt tay nhau thì chỉ có 1 cái bắt tay.
Vậy tổng số lượt bắt tay là: 9 + 8 +7 + 6 + 5 + 4 + 3 + 2 + 1 = 45 (cái)
Đáp số: 45.
Bài 12: ( Xem hình vẽ trong hướng dẫn ) Một sân chơi được lát bằng những viên gạch vuông như trong hình vẽ. Biết rằng diện tích tam giác ABC = 1200 \({{cm^2}}\). Tính diện tích mỗi viên gạch?
Hướng dẫn:
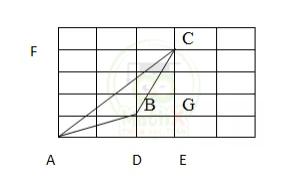
\(\mathbf{S}_{\mathrm{ABC}}=\mathbf{S}_{\mathrm{AFCE}}-\mathbf{S}_{\mathrm{AFC}}-\mathbf{S}_{\mathrm{BCG}}-\mathbf{S}_{\mathrm{BDEG}}-\mathbf{S}_{\mathrm{ABD}}\)
\(\mathrm{S}_{\mathrm{AFCE}}=3\mathrm\ {×}\mathrm{~}4=12\) (đơn vị diện tích)
\(\mathrm{S}_{\mathrm{AFC}}=3\mathrm\ {×}\mathrm{~}4:2=6\) (đơn vị diện tích)
\(\mathrm{S}_{\mathrm{CBG}}=3\mathrm\ {×}\mathrm{~}1:2=1,5\) (đơn vị diện tích)
\(\mathrm{S}_{\mathrm{BDEG}}=1\mathrm\ {×}\mathrm{~}1=1\) (đơn vị diện tích)
\(\mathrm{S}_{\mathrm{ABD}}=2\mathrm\ {×}\mathrm{~}1:2=1\) (đơn vị diện tích)
Vậy:
\(\mathrm{S}_{\mathrm{ABC}}=12-6-1,5-1-1\ =2.5\) (đơn vị diện tích)
1200 (\({{cm^2}}\)) = 2.5 (đơn vị diện tích)
Vậy 1 (đơn vị diện tích) = 1200 : 2.5 = 480 (\({{cm^2}}\))
Diện tích 1 viên gạch = 1 x 1 = 1 (đơn vị diện tích) = 480 (\({{cm^2}}\))
Vậy mỗi viên gạch có diện tích là 480 (\({{cm^2}}\))
Đáp số: 480 \({{cm^2}}\)
Bài 13: A là một số được viết bằng 2012 chữ số 7 : A = 77777…7 (2012 chữ số 7). Hỏi A có chia hết cho 21 hay không?
Hướng dẫn:
A = 7777...7 ( Có 2012 chữ số 7).
Hỏi A có chia hết cho 21 hay không?
21 = 7 x 3. Vậy để A chia hết cho 21 thì A phải đồng thời chia hết 7 và 3.
A chia hết cho 7 vì A chứa toàn 7
Tổng các chữ số của A = 7 x 2012 không chia hết cho 3
Vậy A không chia hết cho 21.
Đáp số: Không.
Bài 14: Tìm hai số biết tổng của chúng bằng 90 và \(\dfrac {1}{5}\) số lớn bằng \(\dfrac {1}{4}\) số bé?
Hướng dẫn:
Đáp án: số lớn = 50 và số bé = 40
Cách làm:
(Bài toán tổng - tỉ số)
\(\dfrac {1}{5}\) số lớn = \(\dfrac {1}{4}\) số bé
số lớn = \(\dfrac {5}{4}\) số bé
Tổng số phần bằng nhau: 5 + 4 = 9 phần
Số lớn là: 90: 9 x 5 = 50
Số bé là: 90 : 9 x 4 = 40
Đáp số: Số lớn = 50; Số bé = 40
Bài 15: Trong hình vuông bên cạnh có 25 hình vuông cạnh 1m.
Hỏi có bao nhiêu hình vuông cạnh 2m?
Hướng dẫn:
Hình vuông 2 x 2 được tạo nên từ 4 hình vuông 1 x 1.
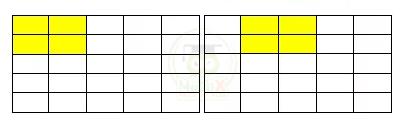
Vậy nếu coi hình vuông 2 x 2 là một ô cửa số 2 x 2 thì :
- Mỗi lần dịch chuyển sang phải 1 ô chúng ta sẽ được 1 hình vuông 2x2. Vậy với 2 dòng đầu tiên tạo được 4 hình vuông 2x2.
- Mỗi lần dịch chuyển xuống đưới một ô và tiến hành dịch sang phải như trên chúng ta lại được 4 hình vuông 2x2. Và có tất cả 4 lần địch xuống dòng. Vậy số ô hình vuông 2 x 2 có thể lập được là: 4 x 4 = 16 (ô).
Đáp số: 16 ô.
Bài 16: Đây là cuộc đời của nhà toán học Điôphăng:
1/6 cuộc đời là thời thơ ấu; 1/12 cuộc đời là thời thanh niên sôi nổi; thêm 1/7 cuộc đời ông chỉ sống độc thân; sau khi lập gia đình 5 năm thì sinh một đứa con trai; con ông chỉ sống bằng một nửa cuộc đời của ông; và ông đã từ trần 4 năm sau khi con ông mất. Hỏi ĐiôPhăng sống bao nhiêu tuổi?
Hướng dẫn:
Gọi a là số tuổi của nhà toán học Điôphăng.
Thời thơ ấu của ông: \(\dfrac {1}{6}\) x a (tuổi)
Cuộc đời thanh niên của ông: \(\dfrac {1}{12}\) x a (tuổi)
Thêm thời gian ông sống đọc thân: \(\dfrac {1}{7}\) x a (tuổi)
Con tai ông sống được: \(\dfrac {1}{2}\) x a (tuổi)
Vậy tổng số thời gian trên chính là số tuổi của Điôphăng:
\(\left({\dfrac{1}{6}}+{\dfrac{1}{12}}+{\dfrac{1}{7}}+{\dfrac{1}{2}}\right)\times a+5+4=a\)
\(\left({\dfrac{7\times2+7+12+6\times7}{12\times7}}\right)\times a+9=a\)
\(\left({\dfrac{75}{84}}\right)\times a+9=a\)
\({\dfrac{25}{28}}\times a+9=a\)
\(9=a-\dfrac{25}{28}\times a\)
\(9={\dfrac{3}{28}}\times a\)
\(a={\dfrac{28\times9}{3}}=84\) (tuổi)
Đáp số: 84 tuổi.
Bài 17: Chu vi hình vuông thứ nhất lớn hơn chu vi hình vuông thứ hai là 12cm, diện tích hình vuông thứ nhất lớn hơn diện tích hình vuông thứ hai là 81 \({{cm^2}}\). Tìm diện tích hình vuông thứ nhất?
Hướng dẫn:
Bài toán yêu cầu là tìm diện tích hình vuông thứ nhất. Vậy để tìm được diện tích, chúng ta cần phải tính được cạnh của hình vuông. Nhưng do chưa biết, nên chúng ta gọi hình vuông thứ nhất có cạnh là a (cm) và hình vuông thứ hai có cạnh là b (cm) để dễ tính.
Chu vi và diện tích hình vuông thứ nhất lần lượt là: 4 x a (cm) và a x a (\({{cm^2}}\))
Chu vi và diện tích hình vuông thứ hai lần lượt là: 4 x b (cm) và b x b (\({{cm^2}}\))
Đầu tiên: Chu vi hình vuông thứ nhất lớn hơn chu vi của hình vuông thứ hai 12 cm
Vậy: 4 x a 4 x b = 12. Rút gọn đi chúng ta còn: a - b = 3 (cm)
Thứ hai: Diện tích hình vuông thứ nhất lớn hơn diện tích hình vuông thứ hai là 81 (\({{cm^2}}\))
nên:
a x a - b x b = 81
Vì a - b = 3 cm, nên b = a - 3. (a hơn b 3 cm).
Sử dụng phương pháp thế:
a x a - (a- 3) x (a - 3) = 81
a x a - (a x a - 3 x a - 3 x a + 9) = 81
a x a - a x a + 6 x a - 9 = 81
6 x a = 81 - 9 = 72
a = 72 : 6 = 12 (cm)
Vậy diện tích hình vuông thứ nhất là: 12 x 12 = 144 (\({{cm^2}}\))
Đáp số: 144 \({{cm^2}}\)
Bài 18: Có một hình vuông và 4 hình tròn được sắp xếp đặt như hình vẽ (xem trong hướng dẫn), bán kính đường tròn bằng 1m. Hãy tính diện tích phần hình vuông nằm ngoài 4 hình tròn đó?
Hướng dẫn:
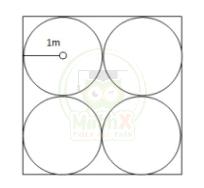
Cần xác định diện tích hình vuông nằm ngoài 4 đường tròn chính là hiệu của diện tích hình vuông lớn với 4 hình tròn đó,
Vậy phải đi tìm diện tích của hình vuông và 4 hình tròn.
Diện tích hình tròn thì có bán kính rồi nên điện tích = 1 x 1 x 3,14 = 3,14 (\({{m^2}}\))
Nhưng 4 hình tròn do có kích thước bán kính bằng nhau nên diện tích 4 hình tròn là như nhau, vậy diện tích của 4 hình tròn là: 3,14 x 4 = 12,56 (\({{m^2}}\))
Vấn đề còn lại là làm sao để tính được điện tích hình vuông. Chú ý chỉ tiết đó là các hình tròn này rất xát nhau, vì vậy cạnh của hình vuông = 2 x đường kính = 2 x 2 = 4 (m)
Điện tích hình vuông là: 4 x 4 = 16 (\({{m^2}}\))
Diện tích phần hình vuông ngoài bốn hình tròn là: 16 - 12,56 = 3,44 (\({{m^2}}\))
Đáp số: 3,44 \({{m^2}}\)
Bài 19: Chia một tam giác đều thành các tam giác đều nhỏ hơn, hỏi có ít nhất bao nhiêu tam giác đều nhỏ?
Hướng dẫn:
Lưu ý: Trong bài này là chia thành các tam giác đều: Có nghĩa là mỗi hình được chia ra phải là một tam giác đều chứ không phải là cắt 1 hình tam giác đều bên trong hình ban đầu, còn các hình khác không quan tâm.
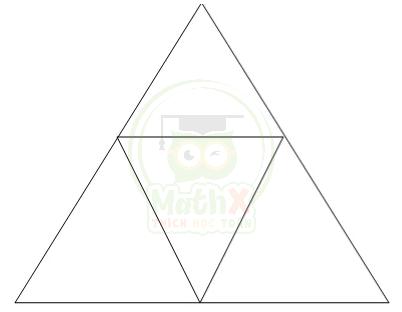
Đáp số: 4.
Bài 20: Một thùng hình hộp chữ nhật có chiều dài 15dm, chiều rộng 12dm và chiều cao 9dm. Một người dùng các khối lập phương có cùng kích thước để xếp kín thùng đó. Tính số hình lập phương ít nhất để có thể làm được như vậy?
Hướng dẫn:
Thể tích của khối hình lập phương đó là:
15 x 12 x 9 = 1620 (\({{dm^3}}\))
Đề yêu cầu tìm số hình lập phương ít nhất có cùng kích thước đề lấp kín hình lập phương trên, vậy tổng thẻ tích các hình lập phương bé phải bằng thê tích hình lập phương lớn và số lượng tìm phải là ít nhất.
Tiến hành phân tích thẻ tích thành tích các thừa số từ bé đến lớn:
1620 = 2 x 2 x 3 x 3 x 3 x 3 x 5
Nhận thấy ngay, trong tích xuất hiện các số hạng giống nhau chính là kích thước của Hình lập phương nhỏ cần tìm, tích còn lại chính là số lượng các hình lập phương đó.
Vậy đề lấp đầy khói hình lập phương ban đầu cần 2 x 2 x 3 x 5 = 60 hình lập phương có kích thước là 3 x 3 x 3 (\({{dm^3}}\))
Đáp số: 60 hình lập phương kích thước là 3 x 3 x 3
Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Và THPT Lương Thế Vinh năm học 2013 - 2014
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS LƯƠNG THẾ VINH để có thể tích lũy thêm nhiều kiến thức và ôn tập hiệu quả hơn.