GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH 2014 2015 - MATHX

 

Để giúp các em học sinh chuẩn bị tốt cho kỳ thi tuyển sinh vào lớp 6 Trường THCS THPT Lương Thế Vinh, MATHX biên soạn đến các em giải chi tiết đề thi tuyển sinh vào 6 môn Toán THCS Lương Thế Vinh 2014-2015. Hy vọng rằng tài liệu giải chi tiết này sẽ là công cụ hữu ích, giúp các em nắm bắt được cấu trúc của đề thi, rèn luyện kỹ năng giải bài một cách linh hoạt và chủ động. Chúc các em học sinh có những kết quả xuất sắc trong kỳ thi sắp tới và đạt được vé vào cổng trường mong muốn.

 

Phụ huynh và các em học sinh xem thêm danh sách đáp án và lời giải chi tiết đề thi vào 6 trường THCS và THPT Lương Thế Vinh các năm tại đây:

 

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2004 - 2005

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2005 - 2006

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2006 - 2007

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2007 - 2008

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2010 - 2011

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2011 - 2012

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2012 - 2013

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2013 - 2014

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2014 - 2015

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2018 - 2019

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2019 - 2020

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2020 - 2021

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2021 - 2022

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2022 - 2023

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2023 - 2024

 

 

Các em học sinh tải đề về luyện tập làm trước khi đối soát với đáp án bên dưới:

 

 

 

 

ĐỀ THI VÀO LỚP 6 TRƯỜNG THCS VÀ THPT LƯƠNG THẾ VINH

(ĐÁP ÁN + LỜI GIẢI CHI TIẾT)

Môn: Toán

Năm học: 2014 - 2015

 

 

Bài 1: Tìm x biết 420 : [75 – (x – 10)] = 21

Hướng dẫn:

\({\dfrac{420}{75-(x-10)}}=21\)

420 = 21 × [75 - (x - 10)]                   // chuyển về và đổi dấu

420 = 21 × (85 - x)                          // Thực hiện bỏ ngoặc

420 : 21 = 85 - x                           // chuyển về và đổi dấu

20 = 85 - x                                  // thực hiện rút gọn

x = 85 - 20 = 65                        // thực hiện tính ra kết quả

Đáp số: 65.

 

 

 

Bài 2: Tổng số tuổi của ông, bố và Nam là 108 tuổi, tuổi của ông gấp $\frac{5}{4}$  tổng số tuổi của Nam và bố, tuổi của bố gấp 3 lần tuổi của Nam. Hỏi số tuổi của từng người?

Hướng dẫn:

Tổng số phần bằng nhau tuổi của Ông so với tổng tuổi của Nam và bố là

4 + 5 = 9 (phần)

Tuổi của ông là: 108 : 9 x 5 = 12 x 5 = 60 ( tuổi )

// Vì ông chiếm 5 phần trong tổng số tuổi của cả 3 người là 108 tuổi.

Vậy bây giờ chỉ còn phải đi tìm của Nam và của Bố khi biết số tuổi của bố gấp 3 lần số tuổi của Nam.

Tổng số tuổi của Nam và Bố là: 108 - 60 = 48 (tuổi)

Tổng số phần bằng nhau là: 3 + 1 = 4 (phần)

// Vì tuổi bố chiếm 3 phần, tuổi nam chiếm 1 phần

Số tuổi của bố là: 48 : 4 x 3 = 12 x 3 = 36 (tuổi)

Số tuổi của Nam là: 48 : 4 x 1= 12 (tuổi)

Đáp số: Ông: 60 tuổi, Bố: 36 tuổi; Nam: 12 tuổi

 

 

 

Bài 3: Bạn Liên đọc một cuốn sách trong ba ngày. Ngày thứ nhất bạn đọc được $\frac{2}{5}$ số trang sách. Ngày thứ hai bạn đọc được $\frac{2}{3}$ số trang sách còn lại. Ngày thứ ba bạn đọc được 60 trang thì đọc xong cuốn sách. Hỏi cuốn sách bạn Liên đọc có bao nhiêu trang?

Hướng dẫn:

Ngày thứ 3 Liên đọc được 60 trang tương ứng với \(\dfrac {1} {3}\) số trang sách còn lại.

Vậy sau ngày thứ nhất, Liên còn phải đọc số trang sách là:

60 x 3 = 180 (trang)

180 trang tương ứng với \(\dfrac {3} {5}\) số trang sách của cả quyền sách, vậy tổng số trangsách Liên đọc là:

180 +3 x 5 = 300 (trang)

Đáp số: 300 trang

 

 

 

Bài 4: Tìm một số tự nhiên có hai chữ số, biết rằng nếu ta viết thêm vào bên trái số đó một chữ số 2 thì ta được số mới mà tổng số đã cho và số mới bằng 346?

Hướng dẫn:

Bài toán quan hệ giữa các chữ số.

Gọi số đã cho ban đầu là \(\overline {ab}\).

Sau khi thêm số 2 vào bên trái ta được số mới: \(\overline {2ab}\)

Theo bài ra, tổng của số mới và số ban đầu bằng 346 nên:

\(\overline {ab}\) + \(\overline {2ab}\) = 346

\(\overline {ab}\) + 200 + \(\overline {ab}\) = 346

2 x \(\overline {ab}\) = 346 - 200 = 146

\(\overline {ab}\) = 146 : 2 = 73

Đáp số: \(\overline {ab}\) = 73.

 

 

 

Bài 5: Bốn bạn Việt, Nam, Chiến, Thắng có tổng cộng 55 cuốn sách. Nếu đem số sách của Việt cộng thêm 5, số sách của Nam trừ đi 5, số sách của Chiến nhân 2, số sách của Thắng chia 3 thì số sách của bốn bạn bằng nhau. Tính số sách ban đầu của mỗi bạn?

Hướng dẫn:

Gọi số sách Việt có là v (quyển)

Số sách Nam có là n (quyển)

Số sách Chiến có là c (quyển)

Số sách Thắng có là t (quyển)

Tổng số sách của bổn bạn là: v + n + e + t = 55 (quyển) (1)

Theo đề bài ra số sách của Việt + 5, số sách Nam - 5, Số sách của Chiến x 2, số sách của Thắng chia 3 thì số sách của 4 bạn bằng nhau nên:

v + 5 = n - 5 = c x 2 = t : 3

Vậy chỉ cần biết số sách của 1 bạn chúng ta sẽ tìm được số sách của các bạn còn lại. Từ biểu thức trên chúng ta có thể rút ra được:

v = c x 2 - 5

n = c x 2 + 5

t = c x 2 x 3 = c x 6

Thế vào (1) chúng ta được: 

(c x 2 - 5) + (c x 2 + 8) + c + (c x 6) = 55

11 x c = 55 vậy e = 5 (quyển)

Chiến có 5 quyển sách

Việt có 5 x 2 - 5 = 5 (quyển sách)

Nam có 5 x 2 + 5 = 15 (quyển sách)

Thắng có 5 x 6 = 30 (quyển sách)

Đáp số: 

Việt: 5 cuốn sách.

Nam: 15 cuốn sách.

Chiến: 5 cuốn sách.

Thắng: 30 cuốn sách.

 

 

 

Bài 6: Tính giá trị biểu thức \(A=17\times\left({\dfrac{1313}{5151}}+{\dfrac{111}{3434}}\right):{\dfrac{177}{12}}\)

Hướng dẫn:

Chúng ta ưu tiên phân tích các số thành tích các thừa số quen thuộc (2,3,5,7,9,11,13,17,19,21...) đặc biệt là 12 và 17.

\(1.313=13\times101\)

5151 = 51 x 101 = 17 x 3 x 101

1111 = 11 x 101

3434 = 34 x 101 = 17 x 2 x 101

12 = 3 x 2 x 2

177 = 3 x 59

Vậy:

\(A=17\times({\dfrac{13\times101}{17\times3\times101}}+{\dfrac{11\times101}{17\times2\times101}})\times{\dfrac{3\times4}{3\times59}}\)

\(A=17\times\left({\dfrac{13}{17\times3}}+{\dfrac{11}{17\times2}}\right)\times{\dfrac{4}{59}}\)

\(A={\bigg(}{\dfrac{17\times13}{17\times3}}+{\dfrac{17\times11}{17\times2}}{\bigg)}\times{\dfrac{4}{59}}\)

\(A=({\dfrac{13}{3}}+{\dfrac{11}{2}})\times{\dfrac{4}{59}}\)

\(A={\dfrac{13\times2+11\times3}{2\times3}}\times{\dfrac{2\times2}{59}}\)

\(A={\dfrac{59}{2\times3}}\times{\dfrac{2\times2}{59}}\)

A = \(\dfrac{2}{3}\)

Đáp số: \(\dfrac{2}{3}\)

 

 

 

Bài 7: Tìm số tự nhiên nhỏ nhất có 4 chữ số khác nhau biết tổng các chữ số của số đó bằng 15 ?

Hướng dẫn:

Đề bài yêu cầu tìm số tự nhiên có 4 chữ số nhỏ nhất. Vậy tính từ trái sang phải các số phải càng nhỏ càng tốt.

Gọi số cần tìm là \(\overline {abcd}\).

Để là số nhỏ nhất thì a phải nhỏ nhất và phải khác 0 (vì là số trên cùng) nên nhỏ nhất chỉ có thể là 1. Vậy a = 1.

b = 0. (là số nhỏ nhất nhưng không phải đứng trên cùng)

còn lại phải tìm c và d.

a + b + c + d = 15           (tổng 4 chữ số bằng 15 theo đề cho)

1 + 0 + e + d = 15           (a,b đã biết theo suy luận ở trên)

c + d = 14 = 5 + 9 = 6 + 8 = 7 + 7           (Lựa chọn ra cặp c và d hợp lý nhất)

Vì số nhỏ nhất nên cặp cd = 59 thỏa mãn.

Vậy số cần tìm là: 1059.

Đáp số: 1059.

 

 

 

Bài 8: Một số tự nhiên được viết bằng 2014 chữ số 7 liên tiếp thì phải cộng thêm ít nhất bao nhiêu đơn vị để được một số chia hết cho 12 ?

Hướng dẫn:

Vì 21 = 7 x 3 nên để chia hết cho 21 thì số đó phải chia hết cho cả 3 lẫn 7.

Số chia hết cho 3 thì tổng phải chia hết cho 3.

Số ban đầu là: 777777...777 (2014 chữ số 7 liên tiếp) có tổng các chữ số là.

7 x 2014 = 14098

14098 lại có tổng các chữ số là 1 + 4 + 0 + 9 + 8 = 22

22 có tổng các chữ số là 2 + 2 = 4 ( không chia hết cho 3)

Gọi a là số cần phải cộng thêm vào số ban đầu, Vậy muốn cộng thêm với a đề chia hết cho 3 thì a phải thuộc trong các số: 2, 5, 8, 11, 14, 17, 20....(cách nhau 3 đơn vị)

Tới đây, chúng ta đã chia nhỏ phạm vi các số thỏa mãn, bây giờ kết hợp thêm điều kiện chia hết cho 7 đề tìm ra số cần cộng thêm.

77777...7777 chắc chẵn sẽ chia hết cho 7, vì vậy muốn cộng thêm một số mà vẫn chia hết cho 7 thì số được cộng thêm phải chia hết cho 7.

Kết hợp điều kiện chia hết cho 3 : a phải thuộc trong các số: 2, 5, 8, 11, 14, 17,....

Thấy được 14 là số thỏa mãn.

Vậy số cộng thêm vào là số 14.

Đáp số: 14.

 

 

 

Bài 9: Lúc 6 giờ sáng một xe máy bắt đầu khởi hành từ Thanh Hóa đi Hà Nội với vận tốc 40 km/giờ. Cùng lúc đó một xe ô tô đi từ Hà Nội đến Thanh Hóa với vận tốc 60 km/giờ. Hỏi mấy giờ hai xe gặp nhau ? Biết quãng đường từ Hà Nội đến Thanh Hóa dài 175 km ?

Hướng dẫn:

Tổng vận tốc 2 xe là: 40 + 60 = 100 (km/giờ)

Thời gian 2 xe gặp nhau là: 175 : 100 = 1,75 giờ

Đổi 1,75 giờ = 1,75 x 60 (phút) = 105 phút = 1 giờ 45 phút.

Đáp số: 1 giờ 45 phút.

 

 

 

Bài 10: Sắp xếp các phân số sau theo thứ tự tăng dần \({\dfrac{5}{9}};{\dfrac{12}{25}};{\dfrac{2}{5}};{\dfrac{14}{27}}\)

Hướng dẫn:

\(\textstyle{\dfrac{5}{9}}={\dfrac{15}{27}}\gt {\dfrac{44}{27}}\) (thực hiện nhân cả tử và mẫu với 3)

\(\dfrac{2}{5}=\dfrac{10}{25}\lt \dfrac{12}{25}\) (thực hiện nhân cả tử và mẫu với 5)

\({\dfrac{12}{25}}\lt {\dfrac{13}{26}}\lt {\dfrac{14}{27}}\) (tử nhỏ hơn mẫu, từ càng lớn thì phân số càng lớn)

Kết luận:

\({\dfrac{2}{5}}\lt {\dfrac{12}{25}}\lt {\dfrac{14}{27}}\lt {\dfrac{5}{9}}\)

Đáp số: \({\dfrac{2}{5}}\lt {\dfrac{12}{25}}\lt {\dfrac{14}{27}}\lt {\dfrac{5}{9}}\)

 

 

 

Bài 11: Một miếng tôn có chu vi 44 dm và chiều dài hơn  chiều rộng 2 dm. Người ta cắt 4 góc của miếng tôn 4 hình vuông bằng nhau, mỗi miếng có diện tích 100 \(cm^2\) rồi gấp lên thành một hình hộp không có nắp. Tính thể tích của hình hộp này.

Hướng dẫn:

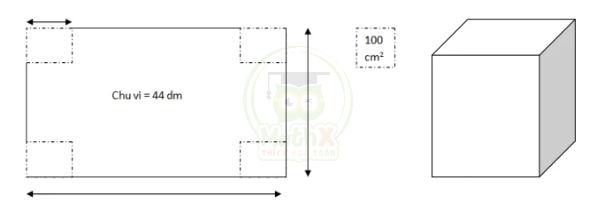
Chiều dài = chiều rộng + 2 dm.

Chu vi = (chiều dài + chiều rộng) x 2

44 = (chiều rộng + 2 + chiều rộng) x 2

44 : 2 = 2 x chiều rộng + 2

22 - 2 = 2 x chiều rộng

20 : 2 = 10 (dm) = chiều rộng.

Chiều dài = chiều rộng + 2 = 10 + 2 = 12 ( dm )

Cạnh của hình vuông bị cắt chính là chiều cao của hình hộp gấp lại.

Diện tích bằng 100 \(cm^2\) nên cạnh = 10 cm = 1 dm

Khi cắt ở 4 góc thì chiều dài và chiều rộng của hình hộp chữ nhật là:

Chiều dài = 12 - 2 x 1 = 10 dm (do cắt ở 2 đầu).

Chiều rộng = 10 - 2 x 1 = 8 dm (do cắt ở 2 đầu)

Thể tích = dài x rộng x cao = 10 x 8 x 1 = 80 (\(dm^3\)) = 80 (lít)

Đáp số: 80 \(dm^3\)

 

 

 

Bài 12: Tìm các chữ số a và b biết số \(\overline {1a89b}\) đồng thời chia hết cho các số 2; 5 và 9 ?

Hướng dẫn:

Số cần tìm chia hết cho 2 vậy b có thể là: 0, 2,4,6,8

Số cần tìm chia hết cho 5 vậy b có thể là: 0 hoặc 5

Vậy b = 0 vì số cần tìm chia hết cho cả 2 và 5. Số cần tìm sẽ là: \(\overline {1a890}\)

Số cần tìm chia hết cho 9 nên tổng các chữ số của số đó phải chia hết cho 9:

1 + a + 8 + 9 + 0= 18 + a phải chia hết cho 9. Vì 18 đã chia hết cho 9 nên a phải là một số chia hết cho 9 nên a = 0 hoặc a = 9.

Vậy có 2 trường hợp thỏa mãn đề ra: 10890 hoặc 19890.

Đáp số: Có 2 trường hợp thỏa mãn để ra: 10890 hoặc 19890.

 

 

 

Bài 13: Cho tam giác ABC có diện tích bằng 240 \(cm^2\), trên cạnh AB lấy điểm M sao cho AB = 3 x AM, trên cạnh CA lấy điểm N sao cho CA = 4 x CN. Tính diện tích tứ giác MNCB ?

Hướng dẫn:

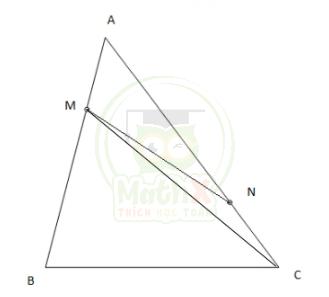
Nối C với M.

Xét tam giác BCM và ACM có chung chiều cao hạ từ đỉnh C xuống AB, có cạnh đáy BM = 2AM (vì AB = 3AM nên BM = 2AM). Vậy

\(\mathrm{S}_{\mathrm{BCM}}=2S_{\mathrm{ACM}}\) (1)

Xét tam giác AMN và MNC có chung chiều cao hạ từ đỉnh M xuống AC, có cạnh đáy AN = 3CN ( vì AC = 4CN nên AN = 3CN). Vậy

\(\mathrm{S}_{\mathrm{AMN}}=3S_{\mathrm{CMN}}\)

\(\mathrm{S}_{\mathrm{CMN}}\ +\mathrm{3S}_{\mathrm{CMN}}=\mathrm{S}_{\mathrm{ACM}}\)

\(4\mathrm{S}_{\mathrm{CMN}}=\mathrm{S}_{\mathrm{ACM}}\)

Diện tích tứ giác MNCB là:

\(\mathrm{S}_{\mathrm{MNCB}}=\mathrm{Sara}+\mathrm{S}_{\mathrm{CMN}}=2\mathrm{S}_{\mathrm{ACM}}+\mathrm{S}_{\mathrm{CMN}}=2\mathrm{x}{\mathrm{4}}{\mathrm{S}}_{\mathrm{CMN}}+\mathrm{S}_{\mathrm{CMN}}=9\mathrm{S}_{\mathrm{CMN}}\)

Diện tích tam giác ABC là: 

\(\mathrm{S}_{\mathrm{ABC}}=\mathrm{S}_{\mathrm{MNCB}}+\mathrm{S}_{\mathrm{AMN}}=9\mathrm{S}_{\mathrm{CMN}}+3\mathrm{S}_{\mathrm{CMN}}=12\mathrm{S}_{\mathrm{CMN}}\)

\(240\mathrm \ {cm}^{2}=12\mathrm{S}_{\mathrm{CMN}}\)

\(\mathrm{S_{CMN}}=240:12=20\mathrm{~(cm^{2})}\)

\(\mathrm{S}_{\mathrm{MNCB}}=\mathrm{9S}_{\mathrm{CMN}}=9\times 20 = 180 \ (cm^2)\)

Đáp số: \(180 \ (cm^2)\)

 

 

 

Bài 14: Cho dãy số 1, 2, 4, 7, 11, 16… Hỏi số hạng tiếp theo của dãy số trên là bao nhiêu?

Hướng dẫn:

1 + 1 = 2 

2 + 2 = 4

4 + 3 = 7

7 + 4  = 11

11 + 5 = 16

Đáp số: 22

 

 

 

Bài 15: Một đoàn tàu đi qua một cây cầu dài 980 m. Biết rằng thời gian bắt đầu từ lúc đầu tàu đến đầu cây cầu và đuôi tàu qua cây cầu là 12 giây, thời gian đuôi tàu ra khỏi cây cầy tính từ lúc tàu bắt đầu đến cầu là 82 giây. Tính chiều dài đoàn tàu ?

Hướng dẫn:

Mô tả bằng hình về chuyển động:

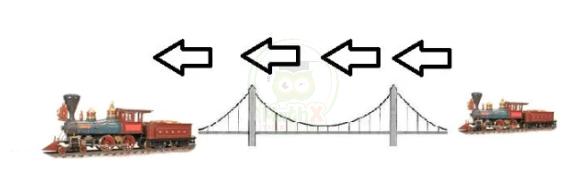
Thời gian đoàn tàu đi hết cây cầu là: 82 — 12 = 70 (giây)

Vận tốc của đoàn tàu là: 980 : 70 = 14 (m/giây)

Quãng đường đoàn tàu đi được cho đến đi đuôi tàu ra khỏi cây cầu là

14 x 82 = 1148 (m)

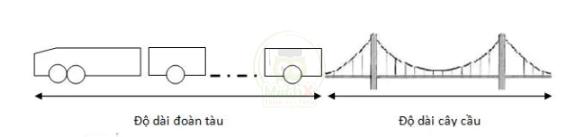
Độ dài đoàn tàu + độ đài cây cầu = quãng đường mà tàu đã đi được tính đến lúc đuôi tàu vừa ra khỏi cầu.

Vậy độ dài đoàn tàu là: 1148 - 980 = 168 (m)

Đáp số: 168 m

 

 

 

Bài 16: Một thửa ruộng hình chữ nhật có chiều dài lớn hơn chiểu rộng 5m. Người ta mở rộng thửa ruộng bằng cách tăng thêm chiều rộng và giữ nguyên chiều dài để được một thửa ruộng hình vuông. Khi đó diện tích thửa ruộng mới lớn hơn diện tích thửa ruộng ban đầu 100 \(m^2\). Tính diện tích của thửa ruộng ban đầu ?

Hướng dẫn:

Vì chiều dài hơn chiều rộng 5m, nên khi tăng chiều rộng lên để được hình vuông thì phần cạnh tăng thêm chính là 5 m. Diện tích phần tăng thêm là 100 \(m^2\), vậy chiều dài của hình chữ nhật đó là: 100 : 5 = 20 (m)

Chiều rộng hình chữ nhật ban đầu là: 20 - 5 = 15 (m)

Diện tích hình chữ nhật ban đầu là: 20 x 15 = 300 (\(m^2\))

Đáp số: 300 \(m^2\)

 

 

 

Bài 17: Nếu đếm các chữ số dùng để ghi tất cả các ngày trong năm 2014 trên tờ lịch treo tường thì kết quả sẽ là bao nhiêu chữ số?

Hướng dẫn:

Tháng 1,3,5,7,8,10,12 là các tháng có 31 ngày.

Tháng 2 năm 2014 có 28 ngày (do không phải năm nhuận)

Tháng 4,6,9,11 là các tháng có 30 ngày.

Từ mùng 1 đến mùng 9 cần dùng: 9 chữ số

--

Từ mùng 10 đến ngày 29 cần dùng: (28 - 10 + 1) x 2 = 38 chữ số

Từ mùng 10 đến ngày 30 cần dùng: (30 - 10 + 1) x 2 = 42 chữ số

Từ mùng 10 đến ngày 31 cần dùng: (31 - 10 + 1) x 2 = 44 chữ số

--

Vậy để ghi các tháng 1,3,5,7,8,10,12 (7 tháng) cần dùng:

7 x (9 + 44) = 371 ( chữ số)

Để ghỉ các tháng 4,6,9,11 (4 tháng) cần dùng:

4 x (9 + 42) = 204 (chữ số)

Để ghi tháng hai cần dùng: 9 + 38 = 47 chữ số

Vậy để ghi tất cả các ngày trong năm 2014 cần dùng số chữ số là

371 + 204 + 47 = 622 chữ số

Đáp số: 622 chữ số.

 

 

 

Bài 18: Tìm ba số tự nhiên biết rằng có một số có ba chữ số, một số có 2 chữ số, một số có một chữ số và trung bình cộng của ba số là 37.

Hướng dẫn:

Tổng của 3 chữ số cần tìm là: 37 x 3 = 111

Trong 3 số có 1 số có 3 chữ số nên số thứ nhất lớn hơn hoặc bằng 100

Trong 3 số có 1 số có 2 chữ số nên số thứ hai lớn hơn hoặc bằng 10

Trong 3 số có 1 số có 1 chữ số nên số thứ ba phải lớn hơn hoặc bằng 1

Vậy tông nhỏ nhất có thể của 3 chữ số là: 100 + 10 + 1 = 111 khi 3 số lần lượt là:

Đáp số: 100; 10; 1.

 

 

 

Bài 19: Xếp các hình lập phương nhỏ cạnh 1 cm thành khối hộp chữ nhật có chiều dài 1 dm, chiều rộng 0,5 dm và chiều cao 0,6 dm. Sau đó ta sơn toàn bộ các mặt của hình hộp chữ nhật. Hỏi có bao nhiêu hình lập phương nhỏ bị tô một mặt?

Hướng dẫn:

Thể tích hình lập phuong nhỏ: 1 x 1 x 1 = 1 (\(cm^3\))

Thể tích hình hộp chữ nhật: 1 x 0,5 x 0,6= 0,3 (\(dm^3\)) = 300 (\(cm^3\))

Số hình lập phương cần để lắp kín hình hộp chữ nhật là: 300 : 1 = 300 hình.

Số hình lập phương cần để phủ 2 mặt đáy hình hộp chữ nhật là:

2 x 5 x 10 = 100 (hình)

Số hình lập phương cần đề phủ 4 mặt bên là:

4 x 6 x 5= 120 (hình)

Các ô ở cạnh ngoài là các ô có thể bị tô 2 hoặc 3 mặt, số ô bị tô 2 đến 3 mặt chính là chu vi của các mặt bên không trùng lên nhau:

(5 + 6) x 2 x 2 + 10 x 4 = 84 (hình)

Số ô bị tô1 mặt là: 100 + 120 - 84 = 136 (hình)

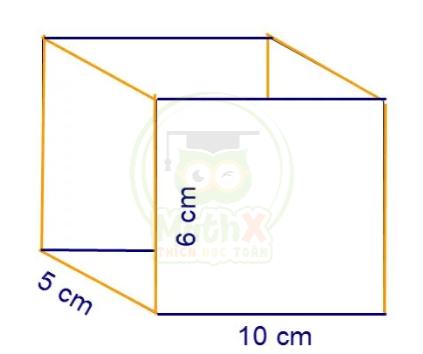
Đáp số: 136 hình.

 

 

 

Bài 20: Cần ít nhất bao nhiêu số 7 để tạo thành các số sao cho tổng các số đó bằng 798 ?

Hướng dẫn:

798 = 777 + 21 = 777 + 7 x 3 = 777 + 7 + 7 + 7

Vậy cần dùng ít nhất 6 số 7.

Đáp số: 6

 

 

Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Và THPT Lương Thế Vinh năm học 2014 - 2015.

 

Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS LƯƠNG THẾ VINH để có thể tích lũy thêm nhiều kiến thức và ôn tập hiệu quả hơn.