
Để giúp các em học sinh chuẩn bị tốt cho kỳ thi tuyển sinh vào lớp 6 Trường THCS Lương Thế Vinh, MATHX biên soạn đến các em giải chi tiết đề thi tuyển sinh vào 6 môn Toán THCS Lương Thế Vinh 2012-2013. Hy vọng rằng tài liệu giải chi tiết này sẽ là công cụ hữu ích, giúp các em nắm bắt được cấu trúc của đề thi, rèn luyện kỹ năng giải bài một cách linh hoạt và chủ động. Chúc các em học sinh có những kết quả xuất sắc trong kỳ thi sắp tới và đạt được vé vào cổng trường mong muốn.
Phụ huynh và các em học sinh xem thêm danh sách đáp án và lời giải chi tiết đề thi vào 6 trường THCS và THPT Lương Thế Vinh các năm tại đây:
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2004 - 2005
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2005 - 2006
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2006 - 2007
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2007 - 2008
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2010 - 2011
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2011 - 2012
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2012 - 2013
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2013 - 2014
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2014 - 2015
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2018 - 2019
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2019 - 2020
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2020 - 2021
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2021 - 2022
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2022 - 2023
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2023 - 2024
Các em học sinh tải đề về luyện tập làm trước khi đối soát với đáp án bên dưới:
Môn: Toán
Năm học: 2012 - 2013
Bài 1: Cho tam giác ABC, gọi M là trung điểm của AB, N là trung điểm của AC. Nếu diện tích tứ giác MNCB = 31,5 \({cm^2}\) thì diện tích tam giác ABC bằng bao nhiêu?
Hướng dẫn:
Nối B với N
\(\mathrm{S}_{\mathrm{AMN}}=\mathrm{S}_{\mathrm{ANB}}\) (Vì 2 tam giác này có cạnh đáy AM = MB)
Nên \(\mathbf{S}_{\mathrm{ANB}}=\mathbf{S}_{\mathrm{AMN}}+\mathbf{S}_{\mathrm{MNB}}=2\mathbf{×}{\mathbf{S}}_{\mathrm{AMN}}=2\mathbf{×}{\mathbf{S}}_{\mathrm{MNB}}\)
Lại có: \(S_{\mathrm{ABN}}=\mathrm{S_{BNC}}=2{S_{MNB}}\)
Chú ý diện tích tứ giác MNBC:
\(\mathrm{S}_{\mathrm{MNBC}}=\mathrm{S}_{\mathrm{MNB}}+\mathrm{S}_{\mathrm{BNC}}=\mathrm{S}_{\mathrm{MNB}}+2\mathrm{×}{\mathrm{S}_{\mathrm{MNB}}}=3\mathrm{×}{\mathrm{S}_{\mathrm{MNB}}}=3\mathrm{×S}_{\mathrm{AMN}}=31.5\)
Vậy \(S_{\mathrm{AMN}}=31.5:3=10.5\;{\mathrm{(cm^{2})}}\)
Cuối cùng là tính diện tích tam giác ABC.
\(\mathrm{S}_{\mathrm{ABC}}=\mathrm{S}_{\mathrm{AMN}}+\mathrm{S}_{\mathrm{MSRRC}}=10.5+31,5=42\ ({\mathrm{cm}}^{2})\)
Đáp số: 42 \({cm}^{2}\)
Bài 2: Một người nói: “tôi sinh sau năm 1976, nhưng trước năm 1984. Cứ 4 năm tôi mới có một lần sinh nhật.”. Hỏi người đó sinh vào ngày nào, tháng nào, năm nào?
Hướng dẫn:
"Cứ 4 năm mới có 1 lần sinh nhật", chứng tỏ người này sinh nào năm nhuận và sinh vào ngày mà 4 năm mới có 1 lần: Ngày 29 tháng 02.
Năm nhuận là năm chia hết cho 4 nhưng không chia hết cho 100 hoặc là năm chia hết cho 400:
Ví dụ các năm như 2004, 2008, 2012, 2016.
Các năm không phải năm nhuận: 1500, 1700, 1900...
Để đơn giản, ở tiểu học chúng ta chỉ nên hiểu năm nhuận sau 4 năm sẽ có một lần và năm đó là năm chia hết cho 4.
Vậy trong các năm từ 1976 đến năm 1984 có năm nào chia hết cho 4: Năm 1980 (số chia hết cho 4 là số có 2 số cuối chia hết cho 4).
Vậy người đó sinh ngày 29 tháng 02 năm 1980.
Đáp số: Ngày 29 tháng 02 năm 1980.
Bài 3: Một hình thang có diện tích 50\({cm^2}\), có đáy lớn = 13m và có chiều cao bằng 5m. Hãy tính độ dài đáy nhỏ?
Hướng dẫn:
Tổng hai đáy của hình thang là:
Đáy lớn + Đáy bé = \({\dfrac{50\times2}{5}}=20\left(m\right)\)
Đáy bé = 20 - Đáy lớn = 20 - 13 = 7 (m)
Đáp số: 7 m.
Bài 4: Tìm 3 số tự nhiên liên tiếp biết tích của chúng bằng 935?
Hướng dẫn:
Phân tích số cần tìm: \(935=5\times187=5\times11\times17\)
Đáp số: 5 x 11 x 17
Bài 5: Cho 3 khối đồng, hình lập phương có độ dài cạnh lần lượt là 3m, 4m, 5m. Người ta đun chảy 3 khối đồng để đúc thành một khối cũng hình lập phương. Tìm cạnh của khối đồng mới đúc?
Hướng dẫn:
Khi đun nóng chảy 3 khối đồng để tạo ra một khối đồng mới thì thể tích khối đồng mới chính bằng tổng của 3 khối đồng được đun nóng chảy.
Thể tích khối đồng được tạo thành là:
3 x 3 x 3 + 4 x 4 x 4 + 5 x 5 x 5 = 27 + 64 + 25 = 216 = 6 x 6 x 6
Vậy cạnh của khối lập phương mới là: 6 x 6 x 6
Đáp số: 6
Bài 6: Hai số a và 5 x a có trung bình cộng bằng 33. Số a bằng bao nhiêu?
Hướng dẫn:
\({\dfrac{a+5\times a}{2}}=33\)
\(6\times a=33\times2=66\)
a = 66 : 6 = 11
Đáp số: 11.
Bài 7: Tìm 3 số lẻ liên tiếp có tổng bằng 1113?
Hướng dẫn:
Thực hiện lấy số tìm chia 3 (nếu tìm 3 số liên tiếp. Nếu đề cho tìm tổng 4 số liên tiếp thì chia 4, 5 số liên tiếp thì chia 5) để tìm ra số trung bình.
1113 : 3 = 371
Vậy các số cần tìm là các số lân cận xung quang của 371. Vì các số cần tìm là các số lẻ nên 3 số cần tìm sẽ là: 169 ; 171; 173 (nhận thấy ngay 171 là số trung bình)
Đáp số: 169; 171; 173
Bài 8: Một chiếc đồng hồ treo tường có kim phút dài 12cm. Hỏi trong thời gian 15 phút đầu mũi kim đó đi được một quãng đường dài bao nhiêu?
Hướng dẫn:
Đồng hỗ treo tường:
Kim giờ quay một vòng là 12 tiếng.
Kim phút quay một vòng là 60 phút
Kim giây quay một vòng là 60 giây
Kim phút quay tạo ra hình tròn có bán kính bằng độ dài kim phút 12cm. Chu vi hình tròn kim phút khi quay tạo ra là:
12 x 2 x 3,14 = 75,36 (cm)
Kim phút quay được 15 phút thì được: \(\dfrac {15}{60}\) = \(\dfrac {1}{4}\) (đường tròn)
Độ dài kim phút đi được là: \(\dfrac {1}{4}\) x 75,36 = 18,84 (cm)
Đáp số: 18,84 cm.
Bài 9: Một bể nước là một hình hộp chữ nhật có chiều dai 2,5m, chiều rộng 1,5m và chiều cao 2m. Một chiếc vòi chảy vào bể cứ 1 giờ chảy được 900 lít nước. Hỏi phải cần bao nhiêu thời gian để vòi nước chảy đầy bể?
Hướng dẫn:
Thể tích bể đựng nước là:
2,5 x 1,5 x 2 = 7,5 (\({{m^3}}\))
Đổi: 7,5 \({{m^3}}\) = 7,5 x 1000 = 7500 lít
Thời gian vòi chảy đầy bể là:
\(7500:900=\dfrac{75}{9}\) = 8\(\dfrac {1}{3}\) (giờ) = 8 giờ + \(\dfrac {1}{3}\) giờ = 8 giờ + 20 phút
Đáp số: 8 giờ 20 phút.
Bài 10: Tìm số A biết : A = 1 + \(\dfrac {1}{4}\) + 3 x 1,25 – 3 : 1,25 + 2 x 1,2?
Hướng dẫn:
\(A=1+\dfrac{1}{4}+3\times1,25-3:1,25+2\times1,2\)
\(A=1+\dfrac{1}{4}+3\times\dfrac{{5}}{4}-3\times\dfrac{{4}}{5}+2\times\dfrac{{6}}{5}\)
\(A=1+\dfrac{1+15}{4}-(\dfrac{12}{5}-\dfrac{12}{5})\)
A = 1 + 4
A = 5
Đáp số: 5.
Bài 11: Tìm số A có hai chữ số, biết rằng A chia hết cho 9 và A + 1 chia hết cho 11.
Hướng dẫn:
Đọc kỹ để và phân tích:
A có 2 chữ số và chia hết cho 9, vậy A có thể là: 18, 36, 45, 54, 63, 72, 81
A + 1 chia hết cho 11. Lựa chọn từ các số ở trên nên A = 54
Đáp số: A = 54.
Bài 12: Bốn hình vuông xếp thành hình chữ T (xem trong hình vẽ hướng dẫn). Mỗi hình vuông có cạnh là 2cm. Tìm diện tích tam giác ABC?
Hướng dẫn:
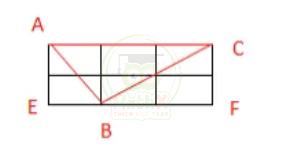
Độ dài các cạnh như sau:
AC = 3 x 2 = 6 (cm)
AE = 2 x 2 = 4 (cm)
EB = 1 x 2 = 2 (cm)
BF = 2 x 2 = 4 (cm)
FC = 2 x 2 = 4 (cm)
\(\mathbf{S}_{\mathrm{ABC}}=\mathbf{S}_{\mathrm{ACFE}}-\mathbf{S}_{\mathrm{AEB}}-\mathbf{S}_{\mathrm{BCF}}\)
\(\mathrm{S}_{\mathrm{ACFE}}=\mathrm{AC}\times\mathrm{CF}=6\times4=24\,({\mathrm{cm}}^{2})\)
\(S_{\mathrm{AEB}}=4\times2:2=4\left({\mathrm{cm}}^{2}\right)\)
Vậy \(\mathrm{S}_{\mathrm{ABC}}=24-4-8=10\left(\mathrm{~cm}^{2}\right)\)
Đáp số: 10 \({~cm}^{2}\)
Bài 13: Một phân số có mẫu số lớn hơn tử số 1 đơn vị. Khi cộng phân số đó với 1 ta được phân số mới có tử số lớn hơn mẫu số 1 đơn vị. Tìm phân số ban đầu?
Hướng dẫn:
Gọi số trên tủ cần tìm là a thì mẫu của phân số là a + 1 (vì ban đầu mẫu hơn tử 1 đơn vị). Phân số cần tìm sẽ là: \(\dfrac {a}{a+1}\)
Khi cộng phân số với 1 ta được phân số mới:
\(\dfrac {a}{a+1}\) + 1 = \(\dfrac {a+a+1}{a+1}\)
Theo đề ra phân số mới có tử lớn hơn mẫu 1 đơn vị nên:
a + a + 1 - (a + 1) = 1
a = 1
Phân số ban đầu là: \(\dfrac {1}{2}\)
Đáp số: \(\dfrac {1}{2}\).
Bài 14: Gọi A là diện tích hình tròn có bán kính 10m , B là diện tích hình chữ nhật có chiều dài cạnh là 20m và chiều rộng là 15,65m. Hãy so sánh A và B?
Hướng dẫn:
Diện tích hình tròn là: \(A=10\times10\ \times3,14=314({m}^{2})\)
Diện tích hình chữ nhật là: B = 20 x 15,65 = 313\(({m}^{2})\)
Vậy A > B
Đáp số: A > B
Bài 15: Mỗi ô dưới đây đều là số có 1 chữ số. Biết rằng cứ 4 ô liên tiếp có tổng bằng nhau. Tìm số ở ô có dấu “?”
_3_ | _7_ | _5_ | ___ | ___ | ___ | ____ | ____ | _?_| ____ |
Hướng dẫn:
| 3 | 7 | 5 | a | 3 | 7 | 5 | a | 3 | 7 |
a có thể là một số bất kì nào cũng được, do 4 số liên tiếp thì tổng bằng nhau nên cứ sau 4 số thì các số sẽ lặp lại.
Đáp số: 3.
Bài 16: Trong một lớp học, số học sinh năm bằng \(\dfrac {1}{4}\) số học sinh nữ và ít hơn số học sinh nữ 4 em. Tìm số học sinh lớp đó.
Hướng dẫn:
Gọi số học sinh của cả lớp là a học sinh.
Hiệu số phần bằng nhau:
4 - 1 = 3 (phần)
Số học sinh nam là:
4 : 3 x 1 = \(\dfrac {4}{3}\) (học sinh).
Số học sinh nữ là: 4 : 3 x 4 = \(\dfrac {16}{3}\) (học sinh).
Bài này đáp án ra số lẻ, không phù hợp với đối tượng nói đến là học sinh. Nên là tìm hai số biết rằng số thứ nhất bằng \(\dfrac {1}{4}\) số thứ hai và hiệu hai số là 4.
Đáp số: \(\dfrac {4}{3}\) và \(\dfrac {16}{3}\)
Bài 17: Rút gọn phân số: \(\dfrac {1111}{98879}\)?
Hướng dẫn:
Từ số nhỏ hơn và nhận thấy ngay tử số chia hết cho 11 nên thực hiện chia từ cho 11:
1111 = 101 x 11
Tiếp theo kiểm tra số lớn có chia hết cho 11 và 101 không thì thấy:
98879 = 11 x 8989 = 11 x 89 x 101
Vậy: \(\dfrac {1111}{98879}\)= \(\dfrac {1}{89}\)
Đáp số: \(\dfrac {1}{89}\).
Bài 18: Trên hình vẽ ta có đường tròn tâm O, bán kính 10cm. Tứ giác OABC là hình vuông với A và C nằm trên đường tròn. Tìm phần diện tích của hình vuông nằm ngoài đường tròn?
Hướng dẫn:
Nhận xét: Phần diện tích hình vuông bên trong hình tròn chiếm \(\dfrac {1}{4}\) diện tích của hình tròn.
Vậy phần diện tích bên ngoài hình tròn của hình vuông = diện tích hình vuông = diện tích \(\dfrac {1}{4}\) hình tròn
Diện tích của hình tròn là: 10 x 10 x 3,14 = 314 \(({cm}^{2})\)
Diện tích hình vuông là: 10 x 10= 100 \(({cm}^{2})\)
Diện tích hình vuông bên ngoài hình tròn là:
100 - 314 : 4= 21,5 \(({cm}^{2})\)
Đáp số: 21,5 \(({cm}^{2})\).
Bài 19: Một hình chữ nhật có diện tích 60 \({{m^2}}\). Nếu tăng chiều dài của nó thêm 1m, còn giữ nguyên chiều rộng thì diện tích tăng thêm 5 \({{m^2}}\). Tính chu vi hình chữ nhật đó?
Hướng dẫn:
Giả sử ban đầu hình chữ nhật có chiều dài là a (m) và chiều rộng là b (m) thì diệntích hình chữ nhật là:
a x b = 60 (\({{m^2}}\))
Sau khi tăng chiều đài lên 1 m thành a + 1 (m) và chiều rộng vẫn là b (m) thì diện tích mới là:
(a + 1) x b = 60 + 5 (vì điện tích tăng thêm 5\({{m^2}}\))
a x b + b = 65
60 + b = 65
b = 5 (m)
Vì a x b = 60 (\({{m^2}}\)) nên a x 5 = 60.
Vậy a = 60 : 5 = 12 (m)
Chu vi hình chữ nhật ban đầu là:
(12 + 5) x 2 = 34 (m)
Đáp số: 34 m.
Bài 20: Tính A = \(\dfrac{1}{{(1 \times 2)}} + \dfrac{1}{{(2 \times 3)}} + \dfrac{1}{{(3 \times 4)}} + \dfrac{1}{{(4 \times 5)}} + ... + \dfrac{1}{{(99 \times 100)}} \)?
Hướng dẫn:
\({\dfrac{1}{2\times3}}={\dfrac{1}{2}}-{\dfrac{1}{3}}\)
\({\dfrac{1}{3\times4}}={\dfrac{1}{3}}-{\dfrac{1}{4}}\)
\({\dfrac{1}{4\times5}}={\dfrac{1}{4}}-{\dfrac{1}{5}}\)
.....
\({\dfrac{1}{99\times100}}={\dfrac{1}{99}}-{\dfrac{1}{100}}\)
Vậy:
\(A={\dfrac{1}{2×3}}+{\dfrac{1}{3×4}}+{\dfrac{1}{4×5}}+...+{\dfrac{1}{99 × 100}}\)
.png)
\(\mathrm{A=1-\,{\dfrac{1}{100}}={\dfrac{100-1}{100}}={\dfrac{99}{100}}}\)
Đáp số: \(\dfrac{{99}}{{100}} \)
Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Và THPT Lương Thế Vinh năm học 2012 - 2013
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS LƯƠNG THẾ VINH để có thể tích lũy thêm nhiều kiến thức và ôn tập hiệu quả hơn.