
Thầy/cô MATHX biên soạn gửi đến các em đề thi tuyển sinh vào lớp 6 Môn Toán trường THCS Lương Thế Vinh có đáp án kèm lời giải chi tiết nhằm giúp các em học sinh làm bài và ôn thi vào 6 hiệu quả.
Phụ huynh và các em học sinh xem thêm danh sách đáp án và lời giải chi tiết đề thi vào 6 trường THCS và THPT Lương Thế Vinh các năm tại đây:
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2004 - 2005
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2005 - 2006
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2006 - 2007
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2007 - 2008
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2010 - 2011
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2011 - 2012
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2012 - 2013
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2013 - 2014
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2014 - 2015
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2018 - 2019
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2019 - 2020
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2020 - 2021
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2021 - 2022
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2022 - 2023
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2023 - 2024
Các em học sinh tải đề về luyện tập làm trước khi đối soát với đáp án bên dưới:
Năm học 2023 - 2024
Thời gian làm bài: 60 phút
Bài 1: Tìm số tự nhiên a biết a x \(2 - 5\dfrac{3}{4} = \dfrac{{57}}{4}\)
Hướng dẫn giải: a × \(2 - 5\dfrac{3}{4} = \dfrac{{57}}{4}\)
a x 2 - \(\dfrac{23}{4}\) = \(\dfrac{57}{4}\)
a × 2 = \(\dfrac{57}{4}\) + \(\dfrac{23}{4}\)
a x 2 = 20
a = 10
Đáp số: a = 10
Bài 2: Tính thể tích bể nước có chiều dài 2,4m, chiều rộng bằng \(\dfrac{2}{3}\) chiều dài và chiều cao 15 dm.
Hướng dẫn giải: Đổi: 2,4 m = 24 dm
Chiều rộng của bể nước là 24 x \(\dfrac{2}{3}\) = 16 (dm)
Thể tích của bể nước là 24 x 16 x 15 = 5760 (dm3)
Đáp số: 5760 (dm3)
Bài 3: Diện tích một mặt hình lập phương là 25 cm2. Hỏi thể tích của hình lập phương đó là bao nhiêu ?
Hướng dẫn giải:
Vì 5 x 5 = 25 nên cạnh của hình lập phương đó là 5 cm
Thể tích của hình lập phương đó là: 5 x 5 x 5 = 125 (cm3)
Đáp số: 125 cm3
Bài 4: Tính 75% của 64
Hướng dẫn giải: 75% của 64 là 64 : 100 x 75 = 48
Đáp số:
Bài 5: Sắp xếp từ bé đến lớn: \(\dfrac{5}{8} \);\(\dfrac{11}{12} \);\(\dfrac{7}{8} \);\(\dfrac{10}{9} \)
Hướng dẫn giải:
Ta có \(\dfrac{5}{8} \)<1; \(\dfrac{11}{12} \)<1;\(\dfrac{7}{8} \)<1;\(\dfrac{10}{9} \)>1
Lại có 1 - \(\dfrac{7}{8} \) = \(\dfrac{1}{8} \) ; 1 - \(\dfrac{11}{12} \) = \(\dfrac{1}{12} \)
Ta có \(\dfrac{1}{8} \)>\(\dfrac{1}{12} \) nên \(\dfrac{7}{8} \)<\(\dfrac{11}{12} \)
Các phân số theo thứ tự từ bé đến lớn là:
\(\dfrac{5}{8} \);\(\dfrac{7}{8} \);\(\dfrac{11}{12} \);\(\dfrac{10}{9} \)
Bài 6: Tìm các số chia hết cho 2 và 5 trong các số 35; 120; 68; 250; 222
Hướng dẫn giải: Các số chia hết cho 2 và 5 là 120 ; 250
Bài 7: Trung bình cộng của hai số là 95. Một trong hai số là 68. Tìm số còn lại.
Hướng dẫn giải:
Tổng của hai số là 95 x 2 = 190
Số còn lại là 190 – 68 = 122
Bài 8: Tính diện tích hình chữ nhật có chiều dài là 20cm và chiều dài hơn chiều rộng 6cm.
Hướng dẫn giải: Chiều rộng hình chữ nhật là 20 – 6 = 14 (cm)
Diện tích hình chữ nhật là 20 x 14 = 280 (cm2)
Bài 9: Tính diện tích phần tô đậm biết diện tích 1 ô là 1cm2
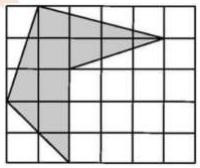
Hướng dẫn giải:
Quan sát hình vẽ ta thấy: Diện tích được tô đậm bằng diện tích của 9 ô vuông và bằng 9cm2
Bài 10: Nhà bác An thu hoạch được một số thóc. Biết 60% số thóc thu hoạch được bằng 1 tấn 200kg. Tính số thóc bác An thu hoạch được.
Hướng dẫn giải:
Đổi 1 tấn 200 kg = 1,2 tấn
Số thóc bác An thu được là 1,2 : 60 x 100 = 2 (tấn)
Bài 11: Tìm một số tự nhiên có hai chữ số. Nếu viết thêm chữ số 4 vào bên trái được số mới gấp 17 lần số ban đầu.
Hướng dẫn giải: Gọi số cần tìm là \(\overline {ab} \)
Theo đề bài ta có: \(\overline {4ab} \) = 17 x \(\overline {ab} \)
400 + \(\overline {ab} \) = 17 x \(\overline {ab} \)
400 = 16 x \(\overline {ab} \)
\(\overline {ab} \) = 400 : 16 = 25
Bài 12: Năm nay con 4 tuổi và mẹ sinh con khi mẹ 26 tuổi. Hỏi sau mấy năm nữa tuổi mẹ gấp 3 lần tuổi con.
Hướng dẫn giải:
Hiệu số tuổi của hai mẹ con không thay đổi là 26 tuổi
Tuổi con khi tuổi mẹ gấp 3 lần tuổi con là:
26 : (3 – 1) x 1 = 13 (tuổi)
Số năm cần tìm là
13 – 4 = 9 (năm)
Đáp số: 9 năm
Bài 13: Tính diện tích hình tròn biết chu vi hình tròn đó là 37,68cm.
Hướng dẫn giải:
Bán kính của hình tròn là:
37,68 : 3,14 : 2 = 6 (cm)
Diện tích hình tròn là
6 x 6 x 3,14 = 113,04 (cm2)
Đáp số: 113,04 cm2
Bài 14: Tính 1,2 + 1,5 + 1,8 + ... + 4,5 + 4,8
Hướng dẫn giải:
Số số hạng trong dãy là:
(4,8 – 1,2) : 0,3 + 1 = 13 (số hạng)
Tổng của dãy số là
(4,8 + 1,2) x 13 : 2 = 39
Bài 15: Có ba vòi chảy vào bể không chứa nước. Nếu vòi 1 và vòi 2 cùng chảy thì 1 giờ 12 phút đầy bể. Nếu vòi 2 và vòi 3 cùng chảy thì 2 giờ đầy bể, nếu vòi 3 và vòi 1 cùng chảy thì 1 giờ 30 phút đầy bể. Hỏi cả 3 vòi cùng chảy thì bao lâu đầy bể?
Hướng dẫn giải:
Đổi 1 giờ 12 phút = \(\dfrac{6}{5} \) giờ
1 giờ 12 phút = \(\dfrac{3}{2} \) giờ
Trong 1 giờ vòi 1 và vòi 2 chảy được 1 : \(\dfrac{6}{5} \) = \(\dfrac{5}{6} \)
Trong 1 giờ vòi 2 và vòi 3 chảy được \(\dfrac{1}{2} \) (bể)
Trong 1 giờ vòi 3 và vòi 1 chảy được 1 : \(\dfrac{3}{2} \) = \(\dfrac{2}{3} \) (bể)
Trong 1 giờ cả ba vòi chảy được (\(\dfrac{5}{6} \) + \(\dfrac{1}{2} \) + \(\dfrac{2}{3} \)) : 2 = 1 (bể)
Vậy cả ba vòi cùng chảy trong 1 giờ thì đầy bể
Bài 16: Lớp 5A phát động phong trào hoa việc tốt. Bạn Linh quyên góp được 2 quyển sách, 3 quyển vở được 16 hoa việc tốt. Bạn Trang quyên góp 10 quyển vở có được số hoa việc tốt bằng bạn Việt góp 4 quyển sách. Hỏi Nam góp 5 quyển sách và 6 quyển vở thì được bao nhiêu hoa việc tốt?
Hướng dẫn giải:
Ta có: 10 quyển vở ứng với 4 quyển sách
=> 5 quyển vở ứng với 2 quyển sách
Lại có 2 quyển sách, 3 quyển vở được 16 hoa việc tốt
=> 8 quyển vở được 16 hoa việc tốt
=> 1 quyển vở được 2 hoa việc tốt
1 quyển sách được số hoa việc tốt là:
(16 – 3 x 2) : 2 = 5 (hoa việc tốt)
Nam được số hoa là:
5 x 5 + 6 x 2 = 37 (hoa việc tốt)
Bài 17: Cho hình vuông như hình vẽ. Tìm diện tích hình vuông phần nằm ngoài hình tròn biết đường chéo AC = 8cm.
.jpg)
Hướng dẫn giải:
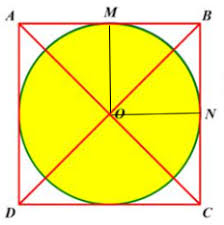
AC và BD cắt nhau tại O
Vậy OA = 4 cm
Diện tích tam giác AOB là 4 x 4 : 2 = 8 (cm2)
Diện tích hình vuông ABCD là 8 x 4 = 32 (cm2)
Diện tích hình vuông MBNO = Diện tích tam giác AOB = 8 (cm2)
Nên tích của bán kính và bán kính là 8
Diện tích hình tròn là: 8 x 3,14 = 25,12 (cm2)
Diện tích phần không tô đậm là:
32 – 25,12 = 6,88 (cm2)
Bài 18: Lớp 5A trồng cây trong 3 ngày. Ngày thứ nhất trồng được \(\dfrac{2}{5}\) tổng số cây. Ngày thứ hai trồng được 28 cây. Ngày thứ ba trồng được \(\dfrac{1}{3}\) số cây đã trồng. Hỏi lớp 5A trồng được bao nhiêu cây?
Hướng dẫn giải:
Ngày thứ ba trồng được \(\dfrac{1}{3}\) số cây đã trồng nên gnayf thứ ba trồng được \(\dfrac{1}{4}\) số cây đã trồng.
Phân số chỉ số cây ngày thứ hai trồng được là:
1 − \(\dfrac{2}{5}\) - \(\dfrac{1}{4}\) = \(\dfrac{7}{20}\) (tổng số cây)
Lớp 5A trồng được tất cả số cây là:
28 : \(\dfrac{7}{20}\) = 80 (cây)
Bài 19: Dùng 7 que diêm thì xếp được tối đa bao nhiêu hình tam giác (phải giữ nguyên trạng thái từng que diêm).
Hướng dẫn giải:
Ta xếp như sau:
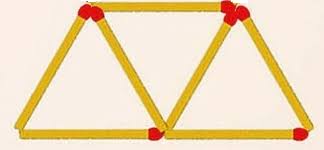
Đáp số: 3 tam giác
Bài 20: Cho hình chữ nhật ABCD có M là trung điểm AB và điểm N nằm trên cạnh AD. Tính tỉ số \(\dfrac{AN}{AD}\) để \({S_{CMN}}\) = \(\dfrac{1}{3}\) x \({S_{ABCD}}\)
Hướng dẫn giải:
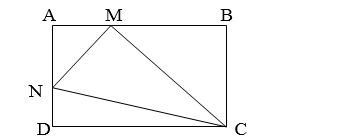
Tổng diện tích các tam giác AMN, MBC, NDC chiếm:
1 - \(\dfrac{1}{3}\) = \(\dfrac{2}{3}\) ( \({S_{ABCD}} \))
Diện tích tam giác MBC chiếm số phần hình chữ nhật ABVD là:
\(\dfrac{{AB}}{2} \times BC \times \dfrac{1}{2} = \dfrac{{AB \times BC}}{4} \) = \(\dfrac{{{S_{ABCD}} }}{4}\)
Vậy tổng diện tích tam giác AMN và NDC chiếm:
\(\dfrac{2}{3} - \dfrac{1}{4} = \dfrac{5}{{12}} \) (\({S_{ABCD}} \))
Tổng diện tích của tam giác ANB và NDC chiếm:
\(\dfrac{{AB \times AN}}{2} + \dfrac{{DC \times DN}}{2} = \dfrac{{AB \times AD}}{2} \) = \(\dfrac{{{S_{ABCD}} }}{2}\)
Diện tích MNB chiếm số phần diện tích ABCD là:
\(\dfrac{1}{2} - \dfrac{5}{{12}} = \dfrac{1}{{12}}\) (\({S_{ABCD}} \))
Vậy:
\(\begin{array}{l} \dfrac{{MB \times AN}}{2} = \dfrac{{AB \times DC}}{2}\\ \dfrac{{AB \times AN}}{4} = \dfrac{{AB \times DC}}{{12}}\\ Vậy: \dfrac{{AN}}{{AD}} = \dfrac{4}{{12}} = \dfrac{1}{3} \end{array} \)
Để giúp học sinh ôn luyện, MATHX có khoá ôn thi vào cấp 2 chất lượng cao với các chuyên đề toán trọng tâm, video chữa đề thi các năm và các đề thi thử.
PHHS xem tại đây:
Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Dân Lập Chuyên Lương Thế Vinh năm học 2023 - 2024.
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS LƯƠNG THẾ VINH để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.
Lưu ý: Các em cần Tạo Tài khoản và Đăng Nhập để có thể xem được những nội dung này