GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH 2011 2012 - MATHX

 

Thầy/cô MATHX biên soạn tổng hợp đến các em học sinh đáp án và lời giải chi tiết đề thi vào 6 trường THCS và THPT Lương Thế Vinh năm học 2011 2012. Tài liệu gồm đề thi và hướng dẫn giải chi tiết, các em xem đề bài và tự làm bài tập ra vở rồi đối chiếu với đáp án để xem kết quả. Chúc các em ôn tập tốt!

 

Phụ huynh và các em học sinh xem thêm danh sách đáp án và lời giải chi tiết đề thi vào 6 trường THCS và THPT Lương Thế Vinh các năm tại đây:

 

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2004 - 2005

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2005 - 2006

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2006 - 2007

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2007 - 2008

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2010 - 2011

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2011 - 2012

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2012 - 2013

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2013 - 2014

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2014 - 2015

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2018 - 2019

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2019 - 2020

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2020 - 2021

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2021 - 2022

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2022 - 2023

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG THCS THPT LƯƠNG THẾ VINH NĂM HỌC 2023 - 2024

 

Các em học sinh tải đề về luyện tập làm trước khi đối soát với đáp án bên dưới:

 

 

 

 

ĐỀ THI VÀO LỚP 6 TRƯỜNG THCS VÀ THPT LƯƠNG THẾ VINH

(ĐÁP ÁN + LỜI GIẢI CHI TIẾT)

Môn: Toán

Năm học: 2011 - 2012

 

 

Bài 1. Trong các số sau, số nào chia hết cho 18?

13040, 104446, 2012, 20112012, 20122011

 

Giải

Ta có: 18 = 9 x 2

Suy ra số chia hết cho 18 sẽ chia hết cho 2 và chia hết cho 9

Suy ra số cần tìm phải là số chẵn và có tổng số các chữ số chia hết cho 9

Ta xét các số trên:

13040: Có tổng số các chữ số = 1 + 3 + 0 + 4 + 0 = 8 không chia hết cho 9 (loại)

104446: Có tổng số các chữ số = 1 + 0 + 4 + 4 + 4 + 6 = 19 không chia hết cho 9 (loại)

2012: Có tổng số các chữ số = 2 + 0 + 1 + 2 = 5 không chia hết cho 9 (loại)

20112012: Có tổng số các chữ số = 2 + 0 + 1 + 1 + 2 + 0 + 1 + 2 = 9 chia hết cho 9 (thỏa mãn)

20122011: Là số lẻ nên không cần tính tổng số các chữ số (loại)

 

 

Đáp án: 20112012

 

 

 

Bài 2. Một người mang trứng đi bán. Sau khi bán được 1/2 số trứng và 35 quả thì số trứng còn lại là 100 quả. Tìm số trứng ban đầu?

 

Giải

Ta tính một nửa số trứng:

35 + 100 = 135 (quả)

Suy ra số trúng ban đầu là:

135 x 2 = 270 (quả)

 

Đáp án: 270 quả

 

 

 

Bài 3. Nhân các số tự nhiên từ 1 đến 20 với nhau. Kết quả là một số có bao nhiêu số 0 đứng cuối?

 

Giải

Trong phép nhân từ 1 đến 20 số 5 xuất hiện 4 lần

5; 10 (5 x 2); 15 (5 x 3); 20 (5 x 4)

Suy ra kết quả của phép tính trên sẽ ra số có 4 chữ số 0 ở tận cùng

 

Đáp án: có 4 chữ số 0 ở tận cùng

 

 

 

Bài 4. Cho một hình vuông. Bên trong vẽ một đường tròn có đường kình bằng cạnh của hình vuông đó. biết diện tích cảu hình tròn là 78,5 cm². Tính diện tích phần hình vuông nằm ngoài hình tròn?

 

Giải

Ta có

Diện tích hình tròn = bán kính x bán kính x 3,14

78,5 = bán kính x bán kính x 3,14

Bán kính x bán kính = 78,5 : 3,14

Bán kính x bán kính = 25

Bán kính = 5 (cm)

 

Diện tích hình vuông = cạnh x cạnh

Mà theo đề bài thì cạnh của hình vuông chính là đường kính của hình tròn

Đường kính hình tròn = bán kính x 2

Suy ra ta có:

Cạnh hình vuông = Đường kính hình tròn = Bán kính x 2 = 5 x 2 = 10 (cm)

Diện tích hình vuông = 10 x 10 = 100 (cm²)

Diện tích phần bôi đen là:

100 - 78,5 = 21,5 (cm²)

 

Đáp án: 21,5 cm²

 

 

 

Bài 5. Tìm số tự nhiên nhỏ nhất gồm 4 chữ số khác nhau sao cho tích 4 chữ số bằng 630?

 

Giải

Tích của 4 số bằng 630 (có số 0 ở hàng đơn vị) nên trong 4 số đó sẽ có một số 5 và một số chẵn

Ta tính được tích của 3 số còn lại:

630 : 5 = 126

Loại số 1 vì nếu có 1 số là 1 thì tích 2 số còn lại sẽ = 126 (không thỏa mãn vì không có 2 số nào có 1 đơn vị có tích bằng 126)

Ta xét số 2

Ta có tích của 2 số còn lại là: 126 : 2 = 63

Ta lại có: 63 = 7 x 9

Ta tìm được 4 số tạo thành số cần tìm là : (5,2,7,9)

Đề bài yêu cầu số cần tìm là bé nhất nên kết quả sẽ là: 2579

 

 

Đáp án: 2579

 

 

 

Bài 6. Trong 2 thùng A và B có tất cả 250 lít dầu. Nếu chuyển 36 lít dầu từ thùng A sang thùng B thì hai thùng có số dầu bằng nhau. Tìm số dầu ban đầu của mỗi thùng?

 

Giải

Nếu mỗi thùng bàng nhau thì mỗi thùng sẽ chứa:

250 : 2 = 125 (lít)

Nếu chuyển 36 lít dầu từ thùng A sang B thì số dầu 2 thùng bằng nhau

Suy ra số dầu thùng A là:

125 + 36 = 161 (lít)

Số dầu thùng B là:

250 - 161 = 89 (lít)

 

 

Đáp án:

Thùng A: 161 lít

Thùng B: 89 lít

 

 

 

Bài 7. Cho phân số  \(\dfrac {6}{29}\) . Hỏi phải thêm vào cả tử và mẫu bao nhiêu đơn vị để được phân số mới là \(\dfrac {1}{2}\)?

 

Giải

Ta có hiệu của mẫu số và tủ số là:

29 - 6 = 23

Khi ta thêm vào tử số và mẫu số cùng một số tự nhiên thì hiệu của mẫu số và tử số vẫn không đổi

Suy ra tử số của phân số mới là:

23 : (2 - 1) x 1 = 23

Suy ra số cần tìm là:

23 - 6 = 17

Kiểm tra lại:

\(\dfrac {6 + 17}{29 + 17} = \dfrac {23}{46} = \dfrac {1}{2} \)

 

Đáp án: 17

 

 

 

Bài 8. Cho phép nhân: \(\overline {ab} \times 5 = \overline {3ab}\) . Tìm a,b (a,b là chữ số)?

 

Giải

\(\overline {ab} \times 5 = \overline {3ab} \\ \Leftrightarrow \overline {ab} \times 5 = 300 + \overline {ab} \\ \Leftrightarrow \overline {ab} \times 4 = 300 \\ \Leftrightarrow \overline {ab} = 300 : 4 = 75\)

 

Vậy

A = 7

B = 5

 

 

Đáp án:

A = 7

B = 5

 

 

 

Bài 9. Một miếng tôn hình chữ nhật có chiều dài là 105 cm,chiều rộng là 85 cm.Ở mỗi góc của hình chữ nhật người ta cắt bổ đi một hình vuông có diện tích là 400 cm², rồi gập lại để tạo thành một hình hộp không có nắp. Tính thể tích của hình hộp đó?

 

Giải

Theo đề bài, khi gập các cạnh vào ta sẽ được một hình hộp chữ nhật có các kích thước như nhau:

Chiều cao của hình hộp chính là cạnh của hình vuống bị cắt đi và = 20 cm (do diện tích hình vuông là 400 cm²) 

Chiều dài của hình hộp = 105 - 20 x 2 = 105 - 40 = 65 (cm) (vì cắt cả 2 bên)

Chiều rộng của hình hộp = 85 - 20 x 2 = 85 - 40 = 45 (cm) (vì cắt cả 2 bên)

Thể tích hình hộp = 20 x 65 x 45 = 58500 (cm³)

 

 

Đáp số: 58500 (cm3)

 

 

Bài 10. Có hai vòi nước cùng chảy vào bể, vòi 1 chảy một mình thì cần 6 giờ mới đầy bể, nếu vòi 2 chảy một mình thì sao 12 giờ mới chảy đầy bể. Hỏi khi hai vòi cùng chảy thì sau bao nhiêu giờ sẽ đầy bể?

 

Giải

Vòi 1 chảy một mình cần 6 giờ mới đầy bể, vậy 1 giờ vòi chảy được \(\dfrac {1}{6}\) bể

Vòi 2 chảy một mình cần 12 giờ mới đầy bể, vậy 1 giờ vòi chảy được \(\dfrac {1}{12}\) bể

Vậy nên 1 giờ cả 2 vòi chảy được:

\(\dfrac {1}{6} + \dfrac {1}{12} = \dfrac {3}{12} = \dfrac {1}{4}\) (bể)

Vậy cả 2 bể cùng chảy thì sau: 4 tiếng sẽ đầy bể

 

 

Đáp án: 4 tiếng

 

 

Bài 11. Một đoàn tàu dài 125m chạy qua một đường hầm với vận tốc 45 km/giờ mất 1 phút 30 giây. Hỏi đường hầm dài bao nhiêu km?

 

Giải

Đổi 45km/h = \(\dfrac {45}{60}\) = 0,75 (km/phút)

Đổi 1 phút 30 giây = 1,5 (phút)

Quãng đường đoàn tàu đi được là:

0,75 x 1,5 = 1,125 (km) = 1125 m

Ta tính được đường hầm dài:

1125 - 125 = 1000 (m) = 1km

 

 

Đáp án: 1km

 

 

 

Bài 12. Một sân chơi được lát bởi những viên gạch vuông có cạnh bằng 30cm. Tính diện tích tam giác ABC?

 

Giải

 

 

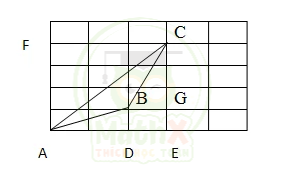
Đổi 30cm = 3dm

Diện tích 1 viên gạch hình vuông là:

3 x 3 = 9 (dm²)

\(\mathrm{S}_{\mathrm{ABC}}=\mathrm{S}_{\mathrm{AECF}}-\mathrm{S}_{\mathrm{AFC}}-\mathrm{S}_{\mathrm{ABD}}-\mathrm{S}_{\mathrm{BCG}}-\ 9\)

\(\mathrm{S}_{\mathrm{AECF}} = 3 \times 3 \times 4 \times 3 = 108\)  (dm²)

\(\mathrm{S}_{\mathrm{AFC}} = 3 \times 3 \times 4 \times 3 : 2 = 54\)  (dm²)

\(\mathrm{S}_{\mathrm{ABD}} = 3 \times 2 \times 3 : 2 = 9\) (dm²)

\(\mathrm{S}_{\mathrm{BCG}} = 3 \times 2 \times 3 : 2 = 9\) (dm²)

Vậy \(\mathrm{S}_{\mathrm{ABC}}= 108 - 54 - 9 - 9 - 9 = 27\) (dm²)

 

 

Đáp án: 27 (dm²)

 

 

Bài 13. lấy số 17 nhân với nhau 2011 lần thì được một số có chữ số tận cùng bằng bao nhiêu?

 

Giải

A = 17 x 17 x 17 x ... x 17 (2011 số 17) 
\(A = \overline {...7} \times \overline {...7} \times \overline {...7} \times ... \times \overline {...7}\)

Ta có:

7 = 7 

\(7 \times 7 = \overline {...9}\)

\(7 \times 7 \times 7 = \overline {...3}\)

\(7 \times 7 \times 7 \times 7 = \overline {...1}\)

Có 2011 : 4 = ..... dư 3 nên chữ số tận cùng là 3.

 

 

Đáp án: 3

 

 

 

Bài 14. Cho tam giác ABC có diện tích là 180 cm2. Điểm M trên cạnh AB sao cho AM = MB, điểm N trên cạnh AC sao cho CN = 2NA. tính diện tích tứ giác BMNC?

 

Giải

Nối B với N

Xét tam giác AMN và tam giác MNB có cạnh đáy AM = BM nên \(\mathrm{S}_{\mathrm{AMN}} = \mathrm{S}_{\mathrm{MNB}}\)

Xét tam giác ABN và tam giác BCN có cạnh đáy CN = 2 x AN nên \(\mathrm{S}_{\mathrm{BNC}} = 2 \times \mathrm{S}_{\mathrm{ABN}}\)

\(\mathrm{S}_{\mathrm{ABC}} = \mathrm{S}_{\mathrm{ABN}} + \mathrm{S}_{\mathrm{BNC}}\)

\(\mathrm{S}_{\mathrm{ABC}} = \mathrm{S}_{\mathrm{ABN}} + 2 \times \mathrm{S}_{\mathrm{ABN}} = 3 \times \mathrm{S}_{\mathrm{ABN}}\)

\(\mathrm{S}_{\mathrm{ABN}} = 180 : 3 = 60\) (cm²)

\(\mathrm{S}_{\mathrm{BNC}} = \mathrm{S}_{\mathrm{ABN}} \times 2 = 60 \times 2 = 120\) (cm²)

\(\mathrm{S}_{\mathrm{MNB}} = \mathrm{S}_{\mathrm{ABN}} : 2 = 60 : 2 = 30\) (cm²)

\(\mathrm{S}_{\mathrm{MNCB}} = \mathrm{S}_{\mathrm{MNB}} + \mathrm{S}_{\mathrm{BCN}} = 120 + 30 = 150\) (cm²)

 

 

Đáp án: 150cm²

 

 

 

Bài 15. cho dãy số: 3,4,6,9,13 … Viết thêm 3 số hạng tiếp theo dãy số đó?

 

Giải

Quy luật: theo nhóm 5 số thì số thứ 4 sẽ là tổng của số 1 và 3, số thứ 5 sẽ là tổng của số 2 và 4

Dãy số tiếp theo sẽ là:

3, 4, 6, 9, 13, 18, 24, 37...

 

Đáp án: 18, 24, 37

 

 

 

Bài 16. Tìm A biết: \(A\left(1\,-\,{\dfrac{1}{4}}\right)\left(1\,-\,{\dfrac{1}{9}}\right)\left(1\,-\,{\dfrac{1}{16}}\right)\left(1\,-\,{\dfrac{1}{25}}\right)=\,\,{\dfrac{8}{5}}\) ?

 

Giải

.\(A\left(1\,-\,{\dfrac{1}{4}}\right)\left(1\,-\,{\dfrac{1}{9}}\right)\left(1\,-\,{\dfrac{1}{16}}\right)\left(1\,-\,{\dfrac{1}{25}}\right)=\,\,{\dfrac{8}{5}} \\ \Leftrightarrow ​​A\left(1\,-\,{\dfrac{1}{4}}\right)\left(1\,-\,{\dfrac{1}{9}}\right)\left(1\,-\,{\dfrac{1}{16}}\right)\left(1\,-\,{\dfrac{1}{25}}\right)= \,1\,{\dfrac{3}{5}} \\ \Leftrightarrow A\times{\dfrac{3}{4}}\times{\dfrac{8}{9}}\times{\dfrac{15}{16}}\times{\dfrac{24}{25}}={\dfrac{8}{5}} \\ \Leftrightarrow A\times{\dfrac{3\times4\times2\times5\times3\times8}{4\times3\times2\times8\times5}}={\dfrac{8}{5}} \\ \Leftrightarrow A\times{\dfrac{3}{5}}={\dfrac{8}{5}} \\ \Leftrightarrow A={\dfrac{8}{3}}\)

 

 

Đáp án: \(A={\dfrac{8}{3}}\)

 

 

 

Bài 17. Sắp xếp các phân số sau theo thứ tự giảm dần: 11/20; 36/79; 49/50?

 

Giải

So sánh \(\dfrac {11}{20}\) với \(\dfrac {36}{79}\)

\({\dfrac{11}{20}}={\dfrac{44}{80}}\gt {\dfrac{43}{79}}\gt {\dfrac{36}{79}}\)

 

So sánh \(\dfrac {11}{20}\) với \(\dfrac {49}{50}\)

\({\dfrac{11}{20}}={\dfrac{55}{100}}\)

\({\dfrac{49}{50}}={\dfrac{96}{100}}\gt {\dfrac{55}{100}}={\dfrac{11}{20}}\)

 

Vậy \(\dfrac{49}{50}\gt \dfrac{11}{20}\gt \dfrac{36}{79}\)

 

 

Đáp án: \(\dfrac{49}{50}\gt \dfrac{11}{20}\gt \dfrac{36}{79}\)

 

 

 

Bài 18. Cho hình thang ABCD, có hai cạnh đáy là AB và CD. biết AB = 5,5 cm và CD = 16,5 cm. So sánh diện tích hai tam giác ABC và ACD?

 

Giải

Hai tam giác ABC và ADC có cùng chiều cao

\(\mathrm{S}_{\mathrm{ABC}}=\mathrm{chiều\;cao}\times\mathrm{AB:2}\)

\(\mathrm{S}_{\mathrm{ADC}}=\mathrm{chiều\;cao}\times\mathrm{DC:2}\)

Vậy \(\mathrm{S}_{\mathrm{ADC}}:\mathrm{S}_{\mathrm{ABC}}=\mathrm{DC}:\mathrm{AB}=16,5:5,5=3\)

\(\mathrm{S}_{\mathrm{ADC}}= 3 \times \mathrm{S}_{\mathrm{ABC}}\)

 

 

Đáp án: \(\mathrm{S}_{\mathrm{ADC}}= 3 \times \mathrm{S}_{\mathrm{ABC}}\)

 

 

 

Bài 19. Một khối gỗ hình lập phương có cạnh 1m. Có thể xẻ khối gỗ ấy thành bao nhiêu khối gỗ hình lập phương, mỗi khối có cạnh là 0,5m?

 

Giải

Thể tích khối lập phương cạnh 1m là: 

1 x 1 x 1 = 1 (m³)

Thể tích khối lập phương cạnh 0,5m là:

0,5 x 0,5 x 0,5 = 0,125 (m³)

Số hình lập phương cạnh 0,5m có thể xẻ được là:

1 : 0,125 = 8 (khối)

 

Đáp án: 8 khối

 

 

 

Bài 20. Người ta dùng các khối gỗ hình lập phương nhỏ cạnh 1m ghép với nhau thành các khối gỗ hình lập phương to cạnh 3m, rồi sơn màu cho các mặt của khối gỗ hình lập phương to. Hỏi có bao nhiêu khối lập phương nhỏ không bị sơn?

 

Giải

Thể tích khối lập phương nhỏ là:

1 x 1 x 1 = 1 (m³)

Thể tích khối lập phương lớn là:

3 x 3 x 3 = 27 (m³)

 

 

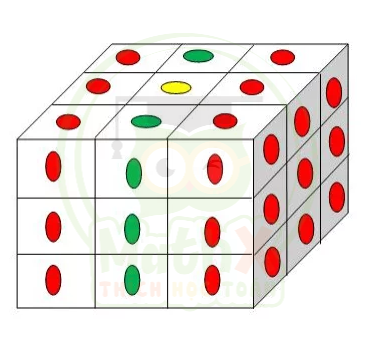
Vậy có tất cả 27 hình lập phương (xem ảnh phía trên)

Nếu quét cả hai mặt bên thì có tất cà 9 + 9 = 18 hình lập phương được quét (màu đỏ)

Quét các ô ở 2 bên màu xanh ta được: 6 hình lập phương

Quét hình ở giữa ta được: 2 hình lập phương

Vậy số hinh lập phương chưa quét là:

27 - 18 - 2 - 6 = 1 (hình)

 

Đáp án: 1 hình

 

 

Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Và THPT Lương Thế Vinh năm học 2011 - 2012

Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS LƯƠNG THẾ VINH để có thể tích lũy thêm nhiều kiến thức và ôn tập hiệu quả hơn.