
Thầy/cô MATHX biên soạn gửi đến các em học sinh và quý phụ huynh đáp án và hướng dẫn giải chi tiết đề thi tuyển sinh vào lớp 6 Môn Toán trường THCS Amsterdam năm học 2023 2024. Chúc các em ôn tập, luyện thi hiệu quả.
Quý phụ huynh và các em học sinh xem thêm hướng dẫn giải đề thi vào 6 trường Amsterdam các năm tại đây:
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2005 2006
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2006 2007
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2007 2008
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2008 2009
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2009 2010
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2010 2011
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2011 2012
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2012 2013
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2013 2014
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2014 2015
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2019 - 2020
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2020 - 2021
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2022 - 2023
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2023 - 2024
NĂM HỌC 2023 – 2024
Câu 1. Thực hiện phép tính: (96 x 0,25 – 2,1: 0,1) + (250 x 0,1 – 80 : 4)
Hướng dẫn giải, đáp án:
(96 x 0,25 – 2,1: 0,1) + (250 x 0,1 – 80 : 4)
= (24 – 21) + (25 – 20)
= 3 + 5 = 8
Đáp số: 8
Câu 2. Biết số \(\overline {224ab}\) chia hết cho 2; 3 và 5. Tìm a x b.
Hướng dẫn giải, đáp án:
Vì số \(\overline {224ab}\) chia hết cho 2 và 5 nên b = 0
Do đó a x b = a x 0 = 0
Đáp số: 0
Câu 3. Trung bình cộng 25 số chẵn liên tiếp bằng 32. Hỏi tỉ số giữa số nhỏ nhất và số lớn nhất là bao nhiêu?
Hướng dẫn giải, đáp án:
Vì 25 số đã cho là 25 số chẵn liên tiếp nên trung bình cộng của 25 số này bằng trung bình cộng của số nhỏ nhất và số lớn nhất.
Tổng số nhỏ nhất và số lớn nhất là: 32 x 2 = 64.
Số chẵn lớn nhất hơn số chẵn bé nhất là: (25 − 1) x 2 = 48.
Số chẵn bé nhất là: (64 – 48) : 2 = 8.
Số chẵn lớn nhất là: 64 – 8 = 56.
Tỉ số giữa số nhỏ nhất và số lớn nhất là \(8:56 = \dfrac{1}{7}\)
Đáp số: \(\dfrac{1}{7}\)
Câu 4. Một khối lượng gạo dự tính đủ cho 15 người ăn trong 14 ngày. Vì số người thực tế nhiều hơn dự kiến nên số gạo đó chỉ đủ ăn trong 6 ngày. Tính số người tăng thêm, biết khẩu phần gạo của mỗi người trong 1 ngày như nhau.
Hướng dẫn giải, đáp án:
1 người ăn hết số gạo trong thời gian là: 14 x 15 = 210 (ngày)
Số người để ăn hết số gạo trong thời gian 6 ngày là: 210 : 6 = 35 (người)
Số người tăng thêm là: 35 – 15 = 20 (người)
Đáp số: 20 người
Câu 5. Một tờ giấy có dạng như hình vẽ:
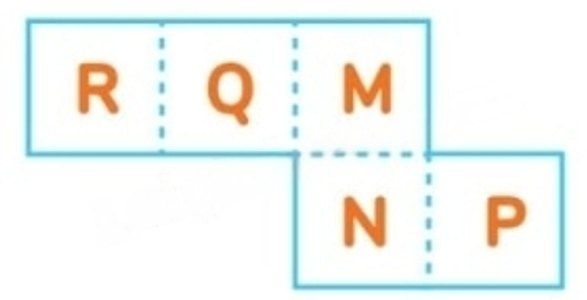
Bạn Chúc gấp tờ giấy theo các nét đứt để làm thành một chiếc hộp hình lập phương không có nắp. Hỏi chữ cái ghi ở đáy của chiếc hộp là chữ cái nào?
Hướng dẫn giải, đáp án:
Ba chữ cái R, Q, M ở ba ô thẳng hàng nên sẽ nằm ở ba mặt bên của hình lập phương.
Do đó chữ cái nằm ở đáy của chiếc hộp là chữ cái N.
Đáp số: Chữ N
Câu 6. Một tờ giấy hình chữ nhật có kích thước 15cm x 20cm. Người ta cắt mỗi góc của tờ giấy đó một hình vuông góc cạnh 5cm. Sau đó gấp phần còn lại thành một hộp giấy hình hộp chữ nhật (không có nắp). Tính tổng diện tích 5 mặt trong của hộp giấy đó.
Hướng dẫn giải, đáp án:
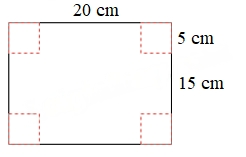
Chiều rộng của hình hộp chữ nhật là: 15 – 5 x 2 = 5 (cm)
Chiều dài của hình hộp chữ nhật là: 20 − 5 × 2 = 10 (cm)
Diện tích xung quanh của hình hộp chữ nhật là: (10 + 5) x 2 × 5 = 150 (cm2)
Diện tích đáy của hình hộp chữ nhật là: 10 x 5= 50 (cm2)
Diện tích cần tính là: 150 + 50 = 200 (cm2)
Đáp số: 200 cm2
Câu 7. Mẹ chia 7 phong bao lì xì chứa số tiền bên trong là: 1; 3; 9; 27; 81: 243; 729 (đơn vị tính: nghìn đồng) cho hai anh em. Sau khi mở ra, Bình nhận thấy số tiền của mình ít hơn của em là 367 nghìn đồng. Hỏi Bình có bao nhiêu bao lì xì?
Hướng dẫn giải, đáp án:
Tổng số tiền mẹ chia cho hai anh em là:
1 + 3 + 9 + 27 + 81 + 243 + 729 = 1093 (nghìn đồng)
Số tiền Bình nhận được là: (1093 – 367) : 2 = 363 (nghìn đồng)
Số tiền em Bình nhận được là: 1093 – 363 = 730 (nghìn đồng)
Vì số tiền của Bình nhận nhỏ hơn phong bao lì xì chứa số tiền 729 nghìn đồng nên em Bình là người nhận được phong bao lì xì 729 nghìn đồng.
Mà em Bình nhận được tổng số tiền là 730 nghìn đồng nên em Bình nhận được 2 bao lì xì là 1 nghìn đồng và 729 nghìn đồng.
Do đó Bình nhận được 5 bao lì xì.
Đáp số: 5 bao lì xì
Câu 8. Cho một số tự nhiên có hai chữ số \(\overline {ab}\) sao cho số đó gấp 8 lần tổng hai chữ số của nó. Tính a x 8 + b x 5.
Hướng dẫn giải, đáp án:
Theo đề bài ta có: \(\overline {ab} = 8 \times \left( {a + b} \right)\)
10 x a + b = 8 x a + 8 x b
2 x a = 7 x b
Mà a, b là các chữ số nên a = 7 và b = 2
Vậy a x 8 + b x 5 = 7 x 8 + 2 x 5 = 66
Đáp số: 66
Bài 9. Cô giáo An cho một số và yêu cầu thực hiện phép tính đem số đó cộng với 5 rồi chia cho 6. Nhưng do nghe nhầm nên An cộng với 6 rồi chia cho 5 nên kết quả sai là 2429. Tìm kết quả đúng.
Hướng dẫn giải, đáp án:
Số trước khi An đem chia cho 5 là: 2429 × 5 = 12145
Số cô giáo cho An là: 12145 – 6 = 12139
Kết quả đúng là: (12139 + 5) : 6 = 2024
Đáp số: 2024
Câu 10. Có một cửa hàng bán xăng dầu vào quý I. Vào quý II, cửa hàng tăng giá 12% so với quý I. Vào quý III, cửa hàng tăng 10% nữa so với quý II. Quý IV, cửa hàng bán xăng giảm 10% so với quý III. Hỏi so với quý I thì giá xăng quý IV của cửa hàng tăng hay giảm bao nhiêu phần trăm.
Hướng dẫn giải, đáp án:
Giá bán xăng của cửa hàng quý II so với quý I là:
100% + 12% = 112% (giá xăng quý I)
Giá bán xăng của cửa hàng quý III so với quý I là:
112% x 110% = 123,2% (giá xăng quý I)
Giá bán xăng của cửa hàng quý IV so với quý I là:
123,2% x 90% = 110,88% (giá xăng quý I)
Giá bán xăng của cửa hàng quý IV tăng so với quý I là:
110,88% – 100% = 10,88% (giá xăng quý I)
Đáp số: tăng 10,88%
Câu 11. Tìm chữ số tận cùng của số: A = 8 x 8 x 8 x ... x 8 + 1 (2024 thừa số 8).
Hướng dẫn giải, đáp án:
Tích của 4 số 8 (8 x 8 x 8 x 8) có tận cùng là chữ số 6.
Mà 2024 chia hết cho 4 nên A có tận cùng là 7.
Đáp số: 7
Câu 12. Cho \( A = \dfrac{1}{{1 \times 300}} + \dfrac{1}{{2 \times 301}} + \dfrac{1}{{3 \times 302}} + .... + \dfrac{1}{{101 \times 400}}\) và
\(B = \dfrac{1}{{1 \times 102}} + \dfrac{1}{{2 \times 103}} + \dfrac{1}{{3 \times 104}} + .... + \dfrac{1}{{299 \times 400}}\)
Tính tỉ số \(\dfrac{A}{B}\)
Hướng dẫn giải, đáp án:
Ta có \(A = \dfrac{1}{{1 \times 300}} + \dfrac{1}{{2 \times 301}} + \dfrac{1}{{3 \times 302}} + .... + \dfrac{1}{{101 \times 400}}\)
\(299 \times A = \dfrac{{299}}{{1 \times 300}} + \dfrac{{299}}{{2 \times 301}} + \dfrac{{299}}{{3 \times 302}} + .... + \dfrac{{299}}{{101 \times 400}}\)
\(299 \times A = 1 - \dfrac{1}{{300}} + \dfrac{1}{2} - \dfrac{1}{{301}} + \dfrac{1}{3} - \dfrac{1}{{302}} + .... + \dfrac{1}{{101}} - \dfrac{1}{{400}}\)
\(299 \times A = (1 + \dfrac{1}{2} + \dfrac{1}{3} + ... + \dfrac{1}{{101}}) - (\dfrac{1}{{300}} + \dfrac{1}{{301}} + \dfrac{1}{{302}} + ... + \dfrac{1}{{400}})\)
Ta có \(B = \dfrac{1}{{1 \times 102}} + \dfrac{1}{{2 \times 103}} + \dfrac{1}{{3 \times 104}} + .... + \dfrac{1}{{299 \times 400}}\)
\(101 \times B = \dfrac{{101}}{{1 \times 102}} + \dfrac{{101}}{{2 \times 103}} + \dfrac{{101}}{{3 \times 104}} + ... + \dfrac{{101}}{{299 \times 400}}\)
\(101 \times B = 1 - \dfrac{1}{{102}} + \dfrac{1}{2} - \dfrac{1}{{103}} + \dfrac{1}{3} - \dfrac{1}{{104}} + ... + \dfrac{1}{{299}} - \dfrac{1}{{400}}\)
\(101 \times B = \left( {1 + \dfrac{1}{2} + \dfrac{1}{3} + ...\dfrac{1}{{299}}} \right) - \left( {\dfrac{1}{{102}} + \dfrac{1}{{103}} + \dfrac{1}{{104}} + ... + \dfrac{1}{{400}}} \right)\)
\(101 \times B = \left( {1 + \dfrac{1}{2} + \dfrac{1}{3} + ... + \dfrac{1}{{101}}} \right) - \left( {\dfrac{1}{{300}} + \dfrac{1}{{301}} + \dfrac{1}{{302}} + ... + \dfrac{1}{{400}}} \right)\)
Suy ra 299 x A = 101 x B hay \(\dfrac{A}{B} = \dfrac{{101}}{{299}}\)
Bài 1. Cho hình vẽ. Biết hình vuông nhỏ có cạnh 4cm, hình vuông lớn có cạnh 6cm. Tính diện tích phần tô đậm.
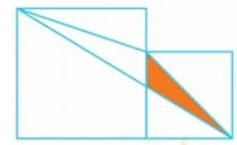
Hướng dẫn giải, đáp án:
Gọi tên các điểm như hình vẽ.
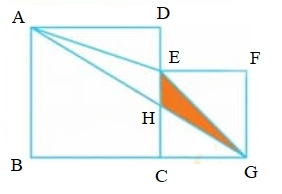
Tổng diện tích hai hình vuông là: 6 x 6 + 4 x 4 = 52 (cm2)
Diện tích tam giác ADE là: 6 x (6 - 4) : 2 = 6 (cm)
Diện tích tam giác EFG là: 4 × 4 : 2 = 8 (cm)
Diện tích tam giác ABG là: 6 x (6 + 4) : 2 = 30 (cm)
Diện tích tam giác AEG là: 52 – 6 – 8 – 30 = 8 (cm)
Xét tam giác AEH và tam giác GEH có chung đáy EH nên \(\dfrac{{{S_{AEH}}}}{{{S_{GEH}}}} = \dfrac{{AD}}{{GC}} = \dfrac{6}{4} = \dfrac{3}{2}\)
Suy ra diện tích tam giác GEH là 8 : (3 + 2) x 2 = 3,2 (cm2)
Đáp số: 3,2 cm2
Bài 2. Lớp 5A có 36 học sinh, cứ 2 bạn ngồi 1 bàn. Cô giáo nhận thấy 50% số bạn nam ngồi
cạnh bạn nữ và 40% số bạn nữ ngồi cạnh bạn nam. Hỏi có bao nhiêu bàn có 2 bạn nữ.
Hướng dẫn giải, đáp án:
Vì 50% số bạn nam ngồi cạnh bạn nữ và 40% số bạn nữ ngồi cạnh bạn nam nên 50% số bạn nam bằng 40% số bạn nữ.
Tỉ số giữa số học sinh nam so với số học sinh nữ là: 40% : 50% = \(\dfrac{4}{5}\)
Số học sinh nữ là: 36 : (4 + 5) × 5 = 20 (học sinh)
Số học sinh nữ ngồi cạnh các bạn nam là: 20 × 40 : 100 = 8 (học sinh)
Số bàn có 2 bạn nữ là: (20 – 8) : 2 = 6 (bàn)
Đáp số: 6 bàn
Bài 3. Đăng và Khoa chạy trên một đường tròn khép kín, hai bạn xuất phát cùng một vị trí nhưng ngược chiều nhau. Đăng và Khoa lần lượt chạy hết đường tròn trong 5 phút và 6 phút. Hỏi sau bao nhiêu lần gặp nhau thì hai bạn gặp nhau lần đầu ở điểm xuất phát (không tính lần gặp nhau khi xuất phát).
Hướng dẫn giải, đáp án:
Khi hai bạn gặp nhau lần đầu tiên ở điểm xuất phát (không tính lần gặp nhau khi xuất phát) thì hai bạn đã chạy được tròn các số vòng.
Do đó thời gian bạn Đăng chạy được sẽ là số chia hết cho 5, thời gian bạn Khoa chạy được sẽ là
số chia hết cho 6.
Mà thời gian hai bạn chạy là bằng nhau (xuất phát cùng lúc) nên khi gặp nhau lần đầu tiên ở điểm
xuất phát (không tính lần gặp nhau khi xuất phát) thì thời gian chạy của hai bạn là số chia hết cho
cả 5 và 6.
Suy ra sau 30 phút, hai bạn gặp nhau lần đầu ở điểm xuất phát (không tính lần gặp nhau khi xuất
phát).
Khi đó, Đăng chạy được 6 vòng và Khoa chạy được 5 vòng.
Tổng hai bạn chạy được 6 + 5 = 11 (vòng)
Do đó, số lần hai bạn gặp nhau trước khi gặp nhau ở điểm xuất phát là: 11 – 1 = 10 (lần).
Các em học sinh xem thêm các đề thi của trường khác tại đây: TỔNG HỢP ĐỀ THI VÀO LỚP 6 MÔN TOÁN MỘT SỐ TRƯỜNG CHẤT LƯỢNG CAO 2023 - 2024
Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Chuyên Amsterdam năm học 2023 - 2024
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS HÀ NỘI AMSTERDAM để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.
Lưu ý: Các em cần Tạo Tài khoản và Đăng Nhập để có thể xem được những nội dung này