HƯỚNG DẪN GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2022 2023 - MATHX

 

 

Trường THPT Chuyên Hà Nội Amsterdam là một trong những trường thuộc Top đầu của Thủ Đô Hà Nội. Chính vì vậy mà đầu vào của trường được chọn lọc rất kĩ càng và bài thi đầu vào của trường khiến không ít phụ huynh trăn trở không đưa ra được hướng ôn luyện cụ thể cho con em mình. Để giúp các em học sinh tự tin bước vào kì thi vào 6, đội ngũ MATHX biên soạn gửi đến phụ huynh và các em học sinh Hướng Dẫn Giải Chi Tiết Đề Thi Vào Lớp 6 THPT Chuyên Hà Nội Amsterdam Năm Học 2022 2023. Chúc các em ôn tập tốt!

 

Phụ huynh và các em học sinh nhấn vào link sau để tải đề về làm trước khi xem đáp án

 

 

Quý phụ huynh và các em học sinh xem thêm hướng dẫn giải đề thi vào 6 trường Amsterdam các năm tại đây:

 

 

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2005 2006

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2006 2007

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2007 2008

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2008 2009

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2009 2010

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2010 2011

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2011 2012

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2012 2013

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2013 2014

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2014 2015

GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2019 - 2020

GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2020 - 2021

GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2022 - 2023

GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2023 - 2024

 

 

 

BÀI KIỂM TRA ĐÁNH GIÁ NĂNG LỰC
TUYỂN SINH VÀO LỚP 6
TRƯỜNG AMS NĂM 2022 - 2023

(đề ghi lại theo trí nhớ của học sinh, có thể có sai số)

 

 

I. Trắc Nghiệm

 

Câu 1. Tính 0,14 x 253 x 3 – 4,2 x 5,3

 

Giải:

0,14 x 253 x 3 – 4,2 x 5,3

= 0,42 x 253 – 0,42 x 53

= 0,42 x (253 – 53)

= 0,42 x 200

= 84

 

Đáp số: 84.

 

 

 

Câu 2. Biết số \(\overline{2022ab}\) chia hết cho cả 5 và 9 (b > 0). Tính a x b.

 

Giải:

Vì số đó chia hết cho 5 mà b > 0

-> b = 5

=>  \(\overline{2022ab}\)  chia hết cho 9

-> 11 + a chia hết cho 9

-> a = 7

Vậy a x b = 7 x 5 = 35

 

Đáp số: 35.

 

 

 

Câu 3. Tính: \(\left( 1-\dfrac{1}{2} \right)\times \left( 1-\dfrac{1}{3} \right)\times \left( 1-\dfrac{1}{4} \right)\times ...\times \left( 1-\dfrac{1}{2022} \right)\)

 

Giải:

\(\begin{align} & \left( 1-\dfrac{1}{2} \right)\times \left( 1-\dfrac{1}{3} \right)\times \left( 1-\dfrac{1}{4} \right)\times ...\times \left( 1-\dfrac{1}{2022} \right) \\ & =\dfrac{1}{2}\times \dfrac{2}{3}\times \dfrac{3}{4}\times ...\times \dfrac{2021}{2022} \\ & =\dfrac{1}{2022} \\ \end{align} \)

 

Đáp số: \(\dfrac {1}{2022}\).

 

 

 

Câu 4. Cho tổng 3 số bằng 2022. Biết số thứ nhất bằng \(\dfrac {1}{3}\)  lần số thứ hai, số thứ ba gấp đôi số thứ nhất. Tìm số lớn nhất.

 

Giải:

Số thứ nhất: I----I

Số thứ hai:   I----I----I----I

Số thứ ba:    I----I----I

Số lớn nhất (chính là số thứ 2) là:

2022 : (1 + 3 + 2) x 3 = 1011

 

Đáp số: 1011.

 

 

 

Câu 5. Ô tô 1 xuất phát từ A cùng lúc với ô tô 2 xuất phát từ B và hai xe gặp nhau tại điểm cách A 140km. Nếu ô tô 1 đi hết quãng đường AB thì hết 8 giờ và ô tô 2 thì mất 7 giờ. Tính quãng đường AB.

 

Giải:

 

 

Xét trên cả quãng đường AB, vận tốc và thời gian là tỉ lệ nghịch.

Tỉ số thời gian của ô tô 1 và ô tô 2 là: \(\dfrac {8}{7}\)

à Tỉ số vận tốc của ô tô 1 và ô tô 2 là: \(\dfrac {7}{8}\)

Khi hai xe xuất phát cùng lúc và đi đến khi gặp nhau thì thời gian đi của hai xe là như nhau

-> quãng đường đi được tỉ lệ thuận với vận tốc.

-> Tỉ số quãng đường đi được của ô tô 1 so với ô tô 2 là  \(\dfrac {7}{8}\)

Do lúc gặp nhau cách A 140km hay tức là ô tô 1 đi được 140km

-> Quãng đường ô tô thứ 2 đi đến khi gặp nhau là:

140 : 7 x 8 = 160 (km)

Quãng đường AB là:

140 + 160 = 300 (km)

 

Đáp số: 300 km.

 

 

 

Câu 6. Hai số có tổng là 4055. Số bé là số có hai chữ số tận cùng là 23. Nếu đổi chỗ hai chữ số tận cùng cho nhau ta được số lớn. Tìm tích hai số đó.

 

Giải:

Vì số bé là số có hai chữ số tận cùng là 23 mà khi đổi chỗ hai chữ số tận cùng cho nhau ta được số lớn

-> Số lớn hơn số bé là:

32 – 23 = 9

Số lớn là:

(4055 + 9) : 2 = 2032

Số bé là:

4055 – 2032 = 2023

Tích của hai số là:

2032 x 2023 = 4110736

 

Đáp số: 4110736.

 

 

Câu 7. Một bể nước dạng hình hộp chữ nhật có kích thước chiều dài 3m, chiều rộng 2m, chiều cao 1,6 m. Người ta mở vòi cho nước chảy vào bể thì sau 1 giờ 15 phút đầy bể. Biết trong 1 giờ vòi chảy được 6756 lít nước. Hỏi ban đầu trong bể có bao nhiêu lít nước?

 

Giải:

Thể tích của bể là: 3 x 2 x 1,6 = 9,6 (m³) = 9600 lít

Đổi 1 giờ 15 phút =  \(\dfrac {5}{4}\) giờ

-> 1 giờ chảy được  \(\dfrac {4}{5}\)  bể

-> Lúc đầu trong bể có số lít nước là:

9600 - 6756 :  \(\dfrac {4}{5}\)  = 1155 (lít)

 

 

Đáp số: 1155 lít.

 

 

 

Câu 8. Có 18 lít nước được đựng trong các chai loại 400ml, 600ml, 1l. Mỗi loại có ít nhất 1 chai. Hỏi có nhiều nhất bao nhiêu chai loại 600ml.

 

Giải:

Đổi 18 lít = 18 000 ml ; 1l = 1000ml

Ta có tổng số lít là 18 000 chia hết cho 3.

Và tổng số lít của các chai 600ml cũng là số chia hết cho 3

-> Tổng số lít ở các loại chai 400ml và 1000ml cũng phải là 1 số chia hết cho 3

Mà để số chai loại 600ml là nhiều nhất có thể thì số chai loại 400ml và 1000ml phải là ít nhất

Ta có 400 + 1000 = 1400 lít chia 3 dư 2

-> cần thêm số chia 3 dư 1

-> cần thêm 1 chai 400ml (chia 3 dư 1)

Số chai loại 600ml là:

Ta có:

(18 000 – 1400 – 400) : 600 = 27 (chai)

Vậy có nhiều nhất 27 chai loại 600ml.

 

 

Đáp số: 27 chai.

 

 

 

Câu 9. Có hai hộp bi A, B, mỗi hộp có 9 viên bi trắng, 9 viên bi đen, 9 viên bi đỏ. Chuyển 10 viên từ A sang B. Hỏi phải chuyển ít nhất bao nhiêu viên từ B sang A để chắc chắn A có ít nhất 8 viên mỗi màu?

 

Giải:

Mỗi hộp có số bi là

9 x 3 = 27 (viên)

Sau khi chuyển 10 viên từ A sang B thì A có số bi là:

27 – 10 = 17 (viên)

Xét trường hợp xấu nhất sau khi chuyển từ B sang A mà trong A có hai loại, mỗi loại 18 viên và 1 loại 7 viên

-> Lúc đó A có

18 x 2 + 7 = 43 (viên)

Vậy sau khi chuyển để chắc chắn A có ít nhất 8 viên mỗi màu thì lúc đó A phải có:

43 + 1 = 44 (viên)

Vậy cần chuyển từ B sang A là:

44 – 17 = 27 (viên)

 

Đáp số: 27 viên.

 

 

 

Câu 10. Ghép 4 mảnh sau thành một hình chữ nhật và tính chu vi của hình đó. Biết mỗi cạnh hình vuông nhỏ có độ dài là 1cm.

 

 

 

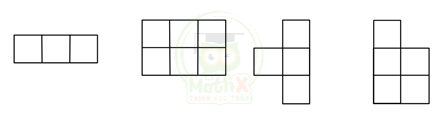
Giải:

Ta có tổng là 18 ô vuông nhỏ

-> diện tích là 18cm²

Ta có:

18 = 1 x 18 = 2 x 9 = 3 x 6

Quan sát các mảnh ta thấy chỉ có thể ghép được hình có kích thước 3 x 6.

Hình ghép được là:

 

 

 

Chu vì hình chữ nhật đó là:

(1 x 6 + 1 x 3) x 2 = 18 (cm)

 

 

 

Đáp số: 18cm.

 

 

 

Câu 11. Cho hình chữ nhật ABCD. Trên cạnh AB lấy điểm P, trên cạnh CD lấy điểm Q sao cho AP = CQ. M là trung điểm BC. Biết AB = 16cm, BC = 12cm. Tính diện tích phần gạch chéo?

 

 

 

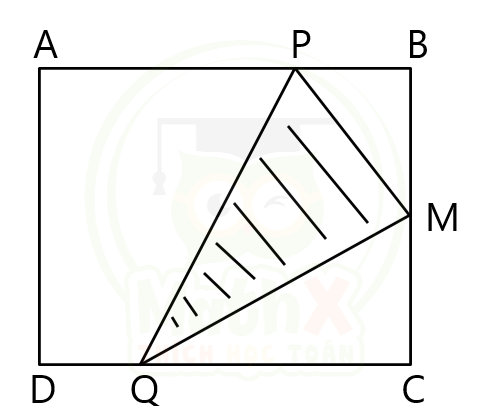
Giải:

Vì AP bằng CQ và AB = CD nên BP = DQ

\(\Rightarrow {{S}_{APQD}}=\text{ }{{S}_{PBCQ}}=\dfrac{1}{2}{{S}_{ABCD}}=\dfrac{1}{2}\times 16\times 12=96\left( c{{m}^{2}} \right)\)

Ta có:

\({{S}_{PBM}}=\dfrac{1}{2}\times PB\times BM\)

\({{S}_{QCM}}=\dfrac{1}{2}\times QC\times MC=\dfrac{1}{2}\times QC\times BM\)  (vì MC = BM)

->  \(\begin{align} & {{S}_{PBM}}+{{S}_{QCM}}=\dfrac{1}{2}\times PB\times BM+\dfrac{1}{2}\times QC\times BM \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\dfrac{1}{2}\times BM\times \left( PB+QC \right) \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\dfrac{1}{2}\times \dfrac{1}{2}\times BC\times \left( PB+QC \right) \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\dfrac{1}{2}{{S}_{PBCQ}}=48\left( c{{m}^{2}} \right) \\ \end{align}\)

 

Vậy diện tích phần gạch chéo là: 96 – 48 = 48 (cm²)

 

Đáp số: 48cm².

 

 

 

Câu 12. Cho 5 số a, b, c, d, e thỏa mãn:

 

\(\dfrac{487}{340}=a+\dfrac{1}{b+\dfrac{1}{c+\dfrac{1}{d+\dfrac{1}{e}}}}\)

 

Vậy a + b + c + d + e = ?

 

Giải:

Ta có:

\(\dfrac{487}{340}=1+\dfrac{147}{340}=1+\dfrac{1}{\dfrac{340}{147}}\)

-> a = 1

-> \(b+\dfrac{1}{c+\dfrac{1}{d+\dfrac{1}{e}}}=\dfrac{340}{147}=2+\dfrac{46}{147}\)

-> b = 2

-> \(c+\dfrac{1}{d+\dfrac{1}{e}}=\dfrac{147}{46}=3+\dfrac{9}{46}\)

-> c = 3

-> \(d+\dfrac{1}{e}=\dfrac{46}{9}=5+\dfrac{1}{9}\)

-> d = 5 và e = 9

Vậy a + b + c + d + e = 1 + 2 + 3 + 5 + 9 = 20

 

Đáp số: 20.

 

 

II. Tự Luận

 

 

Bài 1. Lớp 5A có số học sinh nam gấp đôi số học sinh nữ. Sau khi có 2 học sinh nữ chuyển đi thì số học sinh nam bằng \(\dfrac {5}{2}\)  số học sinh nữ. Hỏi lúc đầu lớp 5A có bao nhiêu học sinh?

 

Giải:

Lúc đầu, số học sinh nữ = \(\dfrac {1}{2}\) số học sinh nam

Sau khi chuyển đi 2 học sinh nữ thì số học sinh nữ =  \(\dfrac {2}{5}\)  số học sinh nam

-> 2 học sinh ứng với:  \(\dfrac{1}{2}-\dfrac{2}{5}=\dfrac{1}{10}\)  (số học sinh nam)

Số học sinh nam là: 2 x 10 =  20 (học sinh)

Số học sinh nữ là: 20 : 2 = 10 (học sinh)

Lúc đầu cả lớp có số học sinh là: 20 + 10 = 30 (học sinh)

 

Đáp số: 30 học sinh.

 

 

 

Bài 2. Có 2 bạn Ngọc và Minh. Minh xuất phát từ A về B. Cùng lúc đó Ngọc đi từ B về A. Lần đầu tiên, 2 bạn gặp nhau ở điểm cách A 7km, rồi Minh đi tiếp về B và quay lại, Ngọc đi tiếp về A rồi quay lại. Lần thứ hai, 2 bạn gặp nhau ở điểm cách B 5 km. Tính quãng đường AB.

 

Giải:

 

 

 

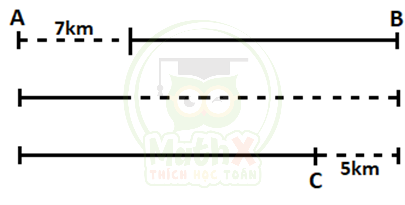
Nhận xét: Từ lúc khởi hành đến lúc 2 người gặp nhau lần thứ hai thì cả hai người đã đi hết 3 lần quãng đường AB.

Ta có sơ đồ thể hiện quãng đường đi được của Minh là nét đứt, Ngọc là nét liền và hai người gặp nhau lần 2 lại C.

Từ sơ đồ ta thấy, cứ mỗi lần hai người đi được 1 quãng đường AB thì Minh đi được 7km. Do đó đến khi gặp nhau lần thứ hai thì Minh đi được:

7 x 3 = 21 (km)

Quãng đường Minh đi được chính bằng quãng đường AB + 5km.

Vậy quãng đường AB dài là: 21 – 5 = 16 (km)

 

Đáp số: 16km.

 

 

 

Bài 3.

Cho hình thang ABCD, lấy điểm M trên AC sao cho AM = 2 x MC. Lấy điểm N trên CD sao cho BDNM là hình thang.

a) So sánh \({{S}_{BDM}}\)  với  \({{S}_{BND}}\)

b) Tính tỉ số   \(\dfrac{{{S}_{ABND}}}{{{S}_{BNC}}}\)

 

Giải:

 

 

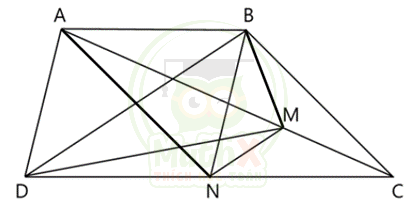
a) Có BDNM là hình thang nên ta có \({{S}_{BDM}}\) = \({{S}_{BDN}}\)

Vì chung đáy BD và chiều cao từ M xuống đáy = chiều cao từ N xuống đáy = chiều cao của hình thang BDNM.

 

b) Ta có  

\({{S}_{BDM}}={{S}_{BDN}}\)  nên   \({{S}_{ABMD}}={{S}_{ABND}}\)

Mà: \({{S}_{ABM}}=2\times {{S}_{BMC}}\) ,  \({{S}_{ADM}}=2\times {{S}_{DMC}}\)   nên

\({{S}_{ABMD}}=2\times \left( {{S}_{BMC}}+{{S}_{DMC}} \right)=2\times \left( {{S}_{BMC}}+{{S}_{MNC}}+{{S}_{DMN}} \right)\)

\({{S}_{ABMD}}=2\times \left( {{S}_{BMC}}+{{S}_{MNC}}+{{S}_{BMN}} \right)\)  (do  \({{S}_{NDM}}={{S}_{BMN}}\) )

\({{S}_{ABMD}}=2\times {{S}_{BNC}}\)

 \(\Rightarrow \frac{{{S}_{ABND}}}{{{S}_{BNC}}}=\dfrac{2}{1}\)

 

Đáp số: .

a.  \({{S}_{BDM}}\) = \({{S}_{BDN}}\)

b. \(\frac{{{S}_{ABND}}}{{{S}_{BNC}}}=\dfrac{2}{1}\)

 

 

Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Chuyên Amsterdam năm học 2022 - 2023

Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS HÀ NỘI AMSTERDAM để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.

Lưu ý: Các em cần Tạo Tài khoản và Đăng Nhập để có thể xem được những nội dung này