
Để giúp các em học sinh chuẩn bị tốt cho kỳ thi tuyển sinh vào lớp 6 Trường Chuyên Amsterdam, Thầy/cô MATHX biên soạn gửi đến phụ huynh và các em hướng dẫn giải chi tiết các dạng bài trong đề thi lên lớp 6 các năm của trường chuyên Hà Nội Amsterdam. Hy vọng rằng tài liệu giải chi tiết này sẽ là công cụ hữu ích, giúp các em nắm bắt được cấu trúc của đề thi, rèn luyện kỹ năng giải bài một cách tốt linh hoạt và chủ động hơn. Chúc các em học sinh có những kết quả xuất sắc trong kỳ thi sắp tới và đạt được vé vào cổng trường mong muốn.
Phụ huynh và các em học sinh xem thêm danh sách đáp án đề thi vào 6 Amsterdam qua các năm tại đây:
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2005 2006
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2006 2007
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2007 2008
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2008 2009
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2009 2010
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2010 2011
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2011 2012
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2012 2013
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2013 2014
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2014 2015
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2019 - 2020
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2020 - 2021
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2022 - 2023
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2023 - 2024
Môn: Toán
Năm học: 2010 - 2011
Bài 1: Tìm A biết: \(\left({\dfrac{242}{363}}+{\dfrac{1616}{2121}}\right)={\dfrac{2}{7}}\times\ A\)
Hướng dẫn:
\(\left({\dfrac{242}{363}}+{\dfrac{1616}{2121}}\right)={\dfrac{2}{7}}\times\ A\)
Thực hiện tối giản các phân số:
\(242\,=\,11\times11\times2\)
\(363\,=\,11\times11\times3\)
\(1616\;=\;101\times16\)
\(2121=101\times21\)
\(\left({\dfrac{242}{363}}+{\dfrac{1616}{2121}}\right)={\dfrac{2}{7}}\times A\)
\(\left({\dfrac{11\times11\times2}{11\times11\times3}}+{\dfrac{101\times16}{101\times21}}\right)={\dfrac{2}{7}}\times A\)
\(\left({\dfrac{2}{3}}+{\dfrac{16}{21}}\right)={\dfrac{2}{7}}\times A\)
\({\dfrac{30}{21}}={\dfrac{2}{7}}\times A\)
\({\dfrac{10}{7}}={\dfrac{2}{7}}\times4\)
A = 10 : 2 = 5
Đáp số: A = 5.
Bài 2: Tính \((48\times0,75-240:10)-(16\times0,5-16:4)\)
Hướng dẫn:
\((48\times0,75-240:10)-(16\times0,5-16+4)\)
\(={\bigg(}48\times{\dfrac{3}{4}}-24{\bigg)}-{\bigg(}16\times{\dfrac{1}{2}}-4{\bigg)}\)
= (36 - 24) - (8 - 4)
= 12 - 4 = 8
Đáp số: 8.
Bài 3: Một hội trường có 270 chỗ ngồi được xếp thành từng hàng và số ghế ở mỗi hàng như nhau. Nếu xếp thêm 2 hàng và số ghế mỗi hàng giữ nguyên thì hội trường có 300 chỗ. Hỏi số hàng ghế lúc đầu là bao nhiêu?
Hướng dẫn:
Số chỗ ngồi tăng thêm là:
300 - 270 = 30 (chỗ)
Số ghế mỗi hàng là:
30 : 2 = 15 (ghế)
Số hàng ghế lúc đầu là:
270 : 15 = 18 (hàng)
Đáp số: 18 hàng.
Bài 4: Trong buổi liên hoan, khi 15 bạn nữ ra về thì trong số bạn còn lại có số nam gấp đôi số nữ. Sau đó lại có 45 bạn nam ra về thì số còn lại có số nữ bằng số nam. Hỏi lúc đầu có bao nhiêu bạn nữ tham gia liên hoan?
Hướng dẫn:
Theo đầu bài, ta có số bạn nam bằng 2 lần số bạn nữa khi có 15 bạn nữ ra về, 45 bạn nam ra về thì số nam bằng số nữ. Do vậy, số bạn nữ còn lại là 45 bạn.
Số bạn nữ lúc đầu là:
45 + 15 = 60 (bạn)
Đáp số: 60 bạn nữ.
Bài 5: Cho hình vuông cạnh 1 dm, nối trung điểm bốn cạnh tạo thành hình vuông thứ hai. Lại nối trung điểm bốn cạnh hình vuông thứ hai tạo thành hình vuông thứ ba, cứ làm như vậy đến hình vuông thứ mười. Tính tổng diện tích của 10 hình vuông đó.
Hướng dẫn:
Hình vuông lớn nhất có diện tích là 1 (dm) x 1(dm) = 1 (\(dm^2\))
Diện tích 4 hình tam giác ở góc có cạnh \(\dfrac {1}{2}\) (dm) sẽ là:
\(4\times{\dfrac{1}{2}}\times{\dfrac{1}{2}}:2={\dfrac{1}{2}}\left(d m^{2}\right)\)
Diện tích hình vuông bên trong là:
1 - \(\dfrac {1}{2}\) = \(\dfrac {1}{2}\) (\(dm^2\))
Vậy diện tích hình vuông bên trong bằng \(\dfrac {1}{2}\) diện tích hình vuông bao ngoài kể với nó.
Theo bài ra, sẽ có tất cả 10 hình vuông nên tổng diện tích của 10 hình vuông đó là:
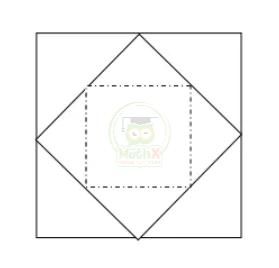
\(A=\mathrm{{1+{\dfrac{1}{2}}+{\dfrac{1}{4}}+{\dfrac{1}{8}}+{\dfrac{1}{8}}+}} \ ... \ + \dfrac{1}{512}\)
A = 1 + \(\dfrac {1}{2}\) x \(\left(1 + \dfrac {1}{2}+\dfrac {1}{4}+\dfrac {1}{8}+ \ ... \ +\dfrac {1}{256}\right)\)
\(A=\ 1+\dfrac{1}{2}\times(\ A - \dfrac{1}{512})\)
\(A=\mathrm{{1+{\dfrac{1}{2}}\times A-{\dfrac{1}{1024}}}}\)
\(A-{\dfrac{A}{2}}=\;1-{\dfrac{1}{1024}}={\dfrac{1023}{1024}}\)
\({\dfrac{A}{2}}={\dfrac{1023}{1024}}\ =\gt A={\dfrac{1023}{1024}}\times2={\dfrac{1023}{512}}\)
Đáp số: \(\dfrac{1023}{512}\)
Bài 6: Bốn người góp tiền mua chung một chiếc Tivi. Người thứ nhất góp số tiền bằng 1/2 số tiền của ba người kia. Người thứ hai góp 1/3 số tiền của ba người còn lại. Người thứ ba góp 1/4 số tiền của ba người kia. Hỏi chiếc Tivi đó có giá bao nhiêu? Biết rằng người thứ tư đã góp 2.600.000 đồng.
Hướng dẫn:
Theo đề bài: Người thứ nhất góp tiền bằng \(\dfrac {1}{3}\) giá tiền chiếc tivi, người thứ hai góp bằng \(\dfrac {1}{4}\) giá tivi, người thứ 3 góp bằng \(\dfrac {1}{5}\) tiền cái tivi. Phân số chỉ 2600000 đồng bằng:
1 - \(\left(\dfrac {1}{3}+\dfrac {1}{4}+\dfrac {1}{5} = \dfrac {13}{60}\right)\) (giá tiền chiếc tivi)
Giá tiền chiếc Tivi đó là:
2600000 : \( \dfrac {13}{60}\) = 12000000 (đồng)
Đáp số: 12000000 đồng.
Bài 7: Cho tam giác ABC có diện tích là 180\(cm^2\). Biết AB = 3BM; AN = NP = PC; QB = QC. Tính diện tích tứ giác MNPQ.
Hướng dẫn:
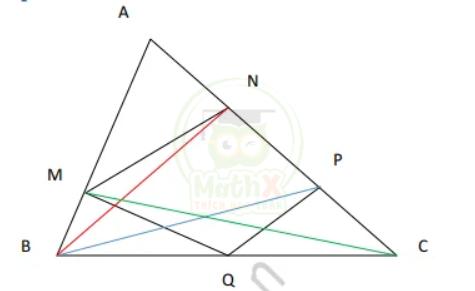
\(S_{ABCD}=180\,c m^{2}\)
AB = 3BM; AN = NP = PC;
QB = QC;
\(S_{ABCD}\) = ?
\(S_{M N P Q}=S_{A B C}-S_{A M N}-S_{B M Q}-S_{C P Q}\)
- Tính diện tích tam giác AMN
Vì tam giác ABN có AN = \(\dfrac {1}{3}\) AC nên \(S_{ABN}\) = \({\dfrac{S_{A B C}}{3}}={\dfrac{180}{3}}=60\,(c m^{2})\)
Vì BM = \(\dfrac {BC}{3}\) nên AM = \(\dfrac {BC}{2}\) => \(S_{AMN}\) = \({\dfrac{2S_{A B C}}{3}}={\dfrac{2 \times 60}{3}}=40\,(c m^{2})\)
- Tính diện tích tam giác CPQ
Vì tam giác BCP có PC = \(\dfrac {1}{3}\)AC nên \(S_{B C P}={\dfrac{S_{A B C}}{3}}={\dfrac{180}{3}}=60\;(c m^{2})\)
Vì BQ = QC nên \(S_{CPQ} = S_{BPQ} \) = \(\dfrac{S_{B G P}}{2}=\dfrac{60}{2}=30\ (c m^{2})\)
- Tính diện tích tam giác BPQ
Vì tam giác BCM có BM = \(\dfrac {1}{3}\)AB nên \(S_{B C M}={\dfrac{S_{A B C}}{3}}={\dfrac{180}{3}}=60\left(c m^{2}\right)\)
Vì BQ = QC nên \({S}_{B M Q}=\,{S}_{M Q C}=\dfrac{S_{B M C}}{2}=\dfrac{60}{2}=30\;(c m^{2})\)
\(S_{M N P Q}=S_{A B C}-S_{A M N}-S_{B M Q}-S_{C P Q}\)
\(S_{M N P Q}=180-40-30-30=80\mathrm{~(cm^{2})}\)
Đáp số: 80 \(cm^2\).
Bài 8: Một sản phẩm trong siêu thị ngày đầu được bán với giá 20.000 đồng. Hôm sau do hạ giá nên số người mua sản phẩm đó tăng thêm 25% và doanh thu cũng tăng thêm 12,5% so với ngày đầu. Hỏi hôm sau giá sản phẩm đó là bao nhiêu?
Hướng dẫn:
Giả sử giá sản phẩm đó lúc đầu là 100%, số người mua là 100%, doanh thu là 100%. Sau khi hạ giá, số người mua 125%, doanh thu 112,5%. Do đó giá sản phẩm mới so với lúc đầu là: 112,5% : 125% = 90%
Giá sản phẩm vào hôm sau là:
20000 : 90% = 18000 (đồng)
Đáp số: 18000 đồng.
Bài 9: Cho dãy số 6; 7; 9; 12; 16 ..... Hỏi số 61 là số hạng thứ bao nhiêu của dãy?
Hướng dẫn:
Nhận xét:
7 = 6 + 1
9 = 7 + 2
12 = 9 + 3
16 = 12 + 4
=> 16 + 5 = 21
21 + 6 = 27
27 + 7 = 34
34 + 8 = 42
42 + 9 = 51
51 + 10 = 61
Vậy số 61 là số hạng thứ 11 của dãy.
Đáp số: 11.
Bài 10: Một sân vận động trong dịp WORLD CUP bán được số vé xem là một số tự nhiên có 5 chữ số bằng 45 lần tích các chữ số của nó. Hỏi số vé bán được là bao nhiêu?
Hướng dẫn:
Gọi số vé bán được là: abcde (a, b, c,d, e là các chữ số và a khác 0). Theo đề bài ta có:
\(\overline {abcde}\) = 45 x a x b x c x d x e
\(\overline {abcde}\) = 5 x 9 x a x b x c x d x e
\(\overline {abcde}\) chia hết cho 5 nên e = 0 hoăc e = 5. Dễ thấy e = 5. Số \(\overline {abcd5}\) là số lẻ nên a, b,c, d, e đầu là các chữ số lẻ.
\(\overline {abcd5}\) = 5 x 9 x a x b x c x d x 5
\(\overline {abcd5}\) = 25 x 9 x a x b x c x d
Do đó, \(\overline {abcd5}\) chia hết cho 25. Mà \(\overline {abcd5}\) = \(\overline {abc}\) x 100 + \(\overline {d5}\). \(\overline {d5}\) chia hết cho 25 và d lẻ => d = 7.
Ta có \(\overline {abcde}\) = \(\overline {abc75}\) chia hết cho 9 nên a + b + c + 7 + 5 = a + b + c + 12 chia hết cho 9. Mà 2 < a + b + c < 28.
Do đó: a + b + c = 6; 15 hoặc 24
Vì a, b, c lẻ nên a + b + c lẻ = > a + b + c = 15
Mà 15 = 1 + 5 + 9 = 1 + 7 + 7 = 3 + 3 + 9 = 3 + 5 + 7 = 5 + 5 + 5
Vì ta có 45 x a x b x c x 7 x 5 < 100000
nên a x b x c < 64. Do đó ta chỉ còn xét hai trường hợp, ba chữ số a, b, c có tổng là 1 + 5 + 9 và 1 + 7 + 7.
Thử chọn thấy 77175 là thích hợp.
Đáp số: 77175.
Bài 1: Lớp 5A có 24 bạn tham gia câu lạc bộ (CLB) cờ vua, 16 bạn tham gia CLB bóng bàn, còn lại 8 bạn không tham gia hai CLB đó. Tính số học sinh của lớp 5A, biết rằng có 8 bạn tham gia cả hai CLB cờ vua và bóng bàn.
Hướng dẫn:
Tổng số học sinh tham gia cả 2 CLB là:
24 + 16 = 40 (học sinh)
Do có 8 bạn tham gia cả 2 CLB nên số học sinh thực tế tham gia 2 CLB sẽ là:
40 - 8 = 32 (học sinh)
Do có 8 bạn không tham gia CLB nên tổng số học sinh cả lớp là:
32 + 8 = 40 (học sinh)
Đáp số: 40 học sinh.
Bài 2: Trên quãng đường AB có hai người đi xe đạp cùng khởi hành từ A đến B. Người thứ nhất đi với vận tốc 10 km/giờ, người thứ hai đi với vận tốc 8 km/giờ. Sau khi đi 2 giờ, người thứ hai tăng vận tốc lên 14 km/giờ nên đuổi kịp người thứ nhất ở địa điểm C. Tính thời gian người thứ hai đã đi trên quãng đường AC và tính quãng đường AB, biết người thứ hai đi từ C đến B mất 2 giờ.
Hướng dẫn:
Ta có sơ đồ:

Nếu người thứ hai đi với vận tốc 14 km/h ngay từ A thì khi người thứ nhất đến C, người thứ hai đã đi qua C một quãng đường là:
(14 - 8) x 2 = 12 (km)
Nếu đi với vận tốc 14 km/h, mỗi giờ người thứ hai đi được nhiều hơn người thứ nhất là 4 km, vậy thời gian người thứ nhất đến C là:
12 : 4 = 3 (giờ)
Như vậy thực tế người thứ hai đi quãng đường AC cũng là 3 giờ.
Người thứ hai đi quãng đường CB mất 2 giờ nên độ dài quãng CB là:
14 x 2 = 28 (km)
Người thứ nhất đi quãng đường AC mất 3 giờ nên độ dài quãng đường AC là:
10 x 3 = 30 (km)
Vậy độ dài quãng đường AB là:
30 + 28 = 58 (km)
Đáp số: 58 km.
Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Chuyên Amsterdam năm học 2010 - 2011.
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS HÀ NỘI AMSTERDAM để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.
Lưu ý: Các em cần Tạo Tài khoản và Đăng Nhập để có thể xem được những nội dung này.