
Để giúp các em học sinh chuẩn bị tốt cho kỳ thi tuyển sinh vào lớp 6 Trường Chuyên Amsterdam, Thầy/cô MATHX biên soạn gửi đến phụ huynh và các em hướng dẫn giải chi tiết các dạng bài trong đề thi lên lớp 6 các năm của trường chuyên Hà Nội Amsterdam. Hy vọng rằng tài liệu giải chi tiết này sẽ là công cụ hữu ích, giúp các em nắm bắt được cấu trúc của đề thi, rèn luyện kỹ năng giải bài một cách tốt linh hoạt và chủ động hơn. Chúc các em học sinh có những kết quả xuất sắc trong kỳ thi sắp tới và đạt được vé vào cổng trường mong muốn.
Phụ huynh và các em học sinh xem thêm danh sách đáp án đề thi vào 6 Amsterdam qua các năm tại đây:
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2005 2006
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2006 2007
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2007 2008
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2008 2009
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2009 2010
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2010 2011
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2011 2012
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2012 2013
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2013 2014
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2014 2015
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2019 - 2020
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2020 - 2021
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2022 - 2023
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2023 - 2024
Môn: Toán
Năm học: 2013 - 2014
Bài 1: Cho các chữ số 1; 2; 3; 4; 5. Hỏi từ các chữ số trên lập được bao nhiêu số chẵn có 3 chữ số khác nhau?
Hướng dẫn:
Vì các số thỏa mãn điều kiện đẻ bài cho là các số chẵn nên số hàng đơn vị có 2 trường hợp thỏa mãn là 2 và 4.
Hàng chục là các số khác hàng đơn vị nên hàng chục có 4 trường hợp.
Hàng trăm khác hàng đơn vị và hàng trục nên hàng đơn vị có 3 trường hợp.
Vậy tổng các chữ số có thể lập được là:
2 x 3 x 4 = 24 (số)
Đáp số: 24 số.
Bài 2: Tìm x biết \(x\times{\dfrac{3+{\dfrac{3}{20}}+{\dfrac{3}{13}}+{\dfrac{3}{2013}}}{5+{\dfrac{5}{20}}+{\dfrac{5}{13}}}}={\dfrac{5}{3}}\,.\)
Hướng dẫn:
Ta có: \({\dfrac{3+{\dfrac{3}{20}}+{\dfrac{3}{13}}+{\dfrac{3}{2013}}}{5+{\dfrac{5}{20}}+{\dfrac{5}{13} +\dfrac{5}{2013}}}}\) = \(\dfrac{3\times\left(\dfrac{1}{20}+\dfrac{1}{13}+\dfrac{1}{2013}\right)}{5\times\left(\dfrac{1}{20}+\dfrac{1}{13}+\dfrac{1}{2013}\right)}=\dfrac{3}{5}\)
Vậy: \(x\times{\dfrac{3}{5}}={\dfrac{5}{3}}=>x=\dfrac{5}{3}:{\dfrac{3}{5}}={\dfrac{5}{3}}\times{\dfrac{5}{3}}={\dfrac{25}{9}}\)
Đáp số: \(x = \dfrac{25}{9}\)
Bài 3: Tổng 3 số chẵn liên tiếp bằng 2028. Tìm ba số đó?
Hướng dẫn:
Số trung bình: 2028 : 3 = 676
Vậy hai số chẵn còn lại là: 676 - 2 = 674 và 676 + 2 = 678.
Đáp số: 674, 676 và 678
Bài 4: Trong một cuộc thi có 60 câu hỏi. Mỗi câu trả lời đúng được \(\dfrac {1}{6}\) điểm, mỗi câu trả lời sai bị trừ \(\dfrac {1}{2}\) điểm. Một bạn học sinh được tổng điểm là 8. Hỏi học sinh đó trả lời đúng mấy câu?
Hướng dẫn:
Gọi số câu trả lời đúng của học sinh số là a (câu) thì số câu trả lời sai sẽ là 60 - a (câu).
Tổng số điểm của học sinh đó là:
\({\dfrac{1}{6}}\times a-{\dfrac{1}{2}}\times(60-a)=8\)
\({\dfrac{a-3\times(60-a)}{6}}=8\)
\(a-180+3a=8\times6\)
4a = 48 + 180
\(4a=228\;\;=\gt a={\dfrac{228}{4}}=57 \ câu\)
Đáp số: 57.
Bài 5: Một người đi từ A đến D phải đi qua hai địa điểm B và C. Vận tốc lúc đi trên các quãng đường AB, BC, CD lần lượt là 9 km/giờ, 12 km/giờ và 18 km/giờ. Lúc về vận tốc trên các quãng đường DC, CB, BA lượt là 9 km/giờ, 12 km/giờ và 18 km/giờ. Cả đi và về hết 5 giờ. Tính độ dài quãng đường AD
Hướng dẫn:
Tổng số thời gian của cả đi và về là:
\({\dfrac{A B}{9}}+{\dfrac{B C}{12}}+{\dfrac{C D}{18}}+{\dfrac{B C}{9}}+{\dfrac{A B}{12}}+{\dfrac{A B}{9}}=5\)
\(\Rightarrow{\dfrac{A B}{6}}+{\dfrac{B C}{6}}+{\dfrac{C D}{6}}=5\)
=> AB + BC + CD = 5 x 6 = 30
=> AD = 30 (km)
Đáp số: 30 km.
Bài 6: Hai máy cùng gặt xong một thửa ruộng hết 12 giờ. Nếu máy I gặt một mình trong 4 giờ, rồi máy II gặt tiếp thêm 9 giờ nữa thì được \(\dfrac{7}{12}\) thửa ruộng. Hỏi nếu máy I gặt một mình thì gặt xong thửa ruộng trong bao lâu?
Hướng dẫn:
Hai người gặt trong 1 giờ được số phần thừa ruộng là: \(\dfrac{1}{12}\) (thửa ruộng)
Hai người gặt trong 4 giờ thì được số m thửa ruộng là:
\(4\times{\dfrac{1}{12}}={\dfrac{1}{3}}\) (thửa ruộng)
Máy hai gặp trong 5 giờ được số thửa ruộng là:
\({\dfrac{7}{12}}-{\dfrac{1}{3}}={\dfrac{1}{4}}\) (thửa ruộng)
Máy hai gặt trong 1 giờ được số thửa ruộng là
\({\dfrac{1}{4}} : 5={\dfrac{1}{4}}\times{\dfrac{1}{5}}={\dfrac{1}{20}}\) (thửa rộng)
Máy một gặt trong 1 giờ được số thửa ruộng là
\({\dfrac{1}{12}}-{\dfrac{1}{20}}={\dfrac{1}{30}}\) (thửa ruộng) => Máy l phải gặt trong 30 giờ mới xong thửa ruộng,
Đáp số: 30 giờ.
Bài 7: Người ta sử dụng các khối lập phương nhỏ có cạnh 1cm để xếp thành một khối lập phương lớn. Biết tổng tất cả các khối lập phương nhỏ xếp trên các cạnh và đỉnh của hình lập phương lớn là 104. Tính thể tích của khối lập phương lớn được tạo thành.
Hướng dẫn:
Tổng số hình lập phương nhỏ xếp trên 1 mặt là:
104 - 4 = 100
Cạnh của hình lập phương lớn là:
100 = 10 x 10. Vậy cạnh = 10 (cm)
Thể tích hình lập phương lớn là:
10 x 10 x 10 = 1000 (\(cm^3\))
Đáp số: 1000 \(cm^3\)
Bài 8: Một cửa hàng định giá bán một chiếc áo lãi 10% so với giá nhập hàng. Trên thực tế chiếc áo chỉ bán được với giá bằng 85% so với giá định bán và đã lỗ 6500 đồng. Hỏi chiếc áo được nhập với giá bao nhiêu?
Hướng dẫn:
Gọi giá nhập của chiếc áo là a (đồng).
Theo dự định cửa hàng định bán lãi 10% nên giá bán dự định là:
110% x a
Thực tế cửa hàng chỉ bán được với giá bằng 85% dự định:
110 x 85% x a = a x 93,5(%)
Phần trăm cửa hàng bị lỗ so với giá nhập là:
a x 100% - a x 93,5% = a x 6,5%.
Cửa hàng bị lỗ 6500 đồng tương đương với 6,5% giá sản phẩm nên giá nhập vào của sản phẩm là:
6500 : 6,5% = 6500 x \(\dfrac{100}{6,5}\) = 100.000 (đồng)
Đáp số: 100.000 đồng
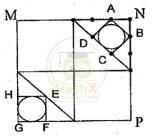
Bài 9: Cho ba hình vuông MNPG, ABCD và HEFG. Tính tỉ số diện tích của hình tròn nằm trong hình vuông ABCD và hình tròn nằm trong hình vuông HEFG.
Hướng dẫn:
Gọi độ dài cạnh của hình vuông MNPG là a (đvđ - đơn vị đo)
Độ dài AN = NB = \(\dfrac{1}{6}\) x a, Độ dài cạnh HG = GF = \(\dfrac{1}{4} \) x a
Xét hình tròn nằm trong hình vuông HEFG có đường kính là \(\dfrac{a}{4} \)
Diện tích hình vuông HEFG là:
\(S_{H E F G}\) = cạnh x cạnh = \(\dfrac{1}{4} \) x \(\dfrac{1}{4} \) = \(\dfrac{1}{16} \)
Xét hình tròn nằm trong hình vuông ABCD. Chúng ta gọi thêm tên 2 điểm D' và C' như hình vẽ.
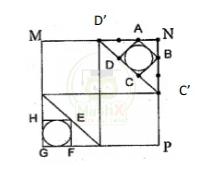
Diện tích tam giác ABN là:
\(S_{ABN}\) = \(\dfrac{AN × NB }{2} \) = \(\dfrac{\dfrac{1}{2}\times\dfrac{1}{6}}{2}=\dfrac{1}{72}\) (đvdt)
Diện tích tam giác ADD' và tam giác BCC':
\(S_{A D D^{\prime}}=\ S_{B C C^{\prime}}=2\times S_{A B N}=2\times{\dfrac{1}{72}}={\dfrac{1}{36}}\) (đvdt)
Diện tích hình vuông ABCD gấp 2 lần diện tích tam giác ADD' vì hai hình này có cùng cạnh nên:
\(S_{A B C D}=2\times S_{A D D'}=2\times{\dfrac{1}{36}}={\dfrac{1}{18}}\) (đvdt)
Tỉ số diện tích hình vuông ABCD và hình vuông HEFG là:
\({\dfrac{S_{A B C D}}{S_{H E F G}}}={\dfrac{1}{18}}:{\dfrac{1}{16}}={\dfrac{1}{18}}\times{\dfrac{16}{1}}={\dfrac{8}{9}}={\dfrac{S_{tròn\;A B C D}}{S_{tròn\,H E F G}}}\)
Vậy tỉ số giữa hai hình tròn là \(\dfrac{8}{9}\).
Đáp số: \(\dfrac{8}{9}\).
Bài 10: Tính tổng: \(A={\dfrac{38}{25}}+{\dfrac{9}{10}}-{\dfrac{11}{15}}+{\dfrac{13}{21}}-{\dfrac{15}{28}}+{\dfrac{17}{36}}-\ldots+{\dfrac{197}{4851}}-{\dfrac{199}{4950}}\)
Hướng dẫn:
\(A={\dfrac{38}{25}}+\left({\frac{9}{10}}-{\dfrac{11}{15}}\right)+\left({\dfrac{13}{21}}-{\dfrac{15}{28}}\right)+\,\ldots+\left({\dfrac{197}{4851}}-{\dfrac{199}{4950}}\right)\)
Số hạng từ 9 đến 199 của phép tính trên là:
N = \(\dfrac{đầu - cuối}{khoảng \ cách \ giữa \ 2 \ số \ kề \ nhau}\) + 1 = \({\dfrac{199-9}{2}}+1=96\) (số)
\({\dfrac{9}{10}}-{\dfrac{11}{15}}={\dfrac{9}{2\times5}}-{\dfrac{11}{3\times5}}\!={\dfrac{1}{5}}\times{\Bigg(}{\dfrac{9}{2}}\!-\!{\dfrac{11}{3}}{\Bigg)}={\dfrac{1}{5}}\times{\dfrac{5}{2\times3}}\!={\dfrac{1}{2\times3}}\)
\({\dfrac{13}{21}}-{\dfrac{15}{28}}={\dfrac{13}{3\times7}}-{\dfrac{15}{4\times7}}={\dfrac{1}{7}}\times\left({\dfrac{13}{3}}-{\dfrac{15}{4}}\right)={\dfrac{1}{7}}\times{\dfrac{7}{3\times4}}={\dfrac{1}{3\times4}}\)
.....
\(A={\dfrac{38}{25}}+{\dfrac{1}{2\times3}}+{\dfrac{1}{3\times4}}+\ldots+{\dfrac{1}{6\times96}}={\dfrac{38}{25}}+{\dfrac{1}{6}}+{\dfrac{1}{12}}+\ldots+{\dfrac{1}{576}}\)
\(A={\dfrac{38}{25}}+{\dfrac{1}{2\times3}}+{\dfrac{1}{3\times4}}+\ldots+{\dfrac{1}{49\times50}}\)
\(A={\dfrac{38}{25}}+\left({\dfrac{1}{2}}-{\dfrac{1}{3}}+{\dfrac{1}{3}}-{\dfrac{1}{4}}+{\dfrac{1}{4}}-{\dfrac{1}{5}}+\ldots+{\dfrac{1}{49}}-{\dfrac{1}{50}}\right)\)
\(A={\dfrac{38}{25}}+{\dfrac{1}{2}}-{\dfrac{1}{50}}={\dfrac{76+25-1}{50}}={\dfrac{100}{50}}\)
A = 2
Đáp số: A = 2.
Bài 1: Cho hình chữ nhật ABCD, F là một điểm bất kì trên cạnh AD, BF cắt CD kéo dài tại điểm E. Nối điểm A với điểm E. Tính diện tích tam giác AEF, biết AF = 3 cm, BC = 5 cm, AB = 7 cm.
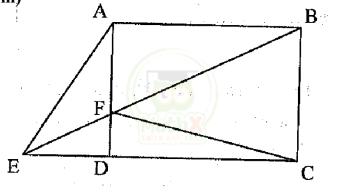
Hướng dẫn:
Ta có:
S(ABE) = S(ABC) = \(\dfrac{1}{2}\) AB x BC = 17,5 (\(cm^2\))
S(ABF) = \(\dfrac{1}{2}\) AB x AF = 10,5 (\(cm^2\))
Suy ra diện tích tam giác AEF là:
S(AEF) = S(ABE) – S(ABF) = 17,5 – 10,5 = 7 (\(cm^2\))
Đáp số: 7 \(cm^2\)
Bài 2: Tìm số có 4 chữ số khác nhau \({\overline{{a b c d}}}+{\overline{{b c d}}}+{\overline{{c d}}}+d=8098\)
Hướng dẫn:
Điều kiện: a, b, c khác 0
Ta có: \({\overline{{b c d}}}\geq123\) nên \({\overline{{a b c d}}}\lt 8098-123\lt 8000\), suy ra a < 8.
\(\overline{{{b c d}}}+\overline{{{c d}}}+d\le987+87+7=1081\) nên \({\overline{{a b c d}}}\geq8098-1081=7017\), suy ra a =7
Khi đó \({2\times{\overline{{b c d}}}}+{\overline{{c d}}}+d=1098\) hay \(200\times b+30\times c+4\times d=1098\)
Suy ra \(b\lt 1098:200\lt 6\) hay b \(\le 5\)
Lại có \(30\times c+4\times d\leq30\times9+4\times8=302\) nên \(200\times b\geq1098-302=796\), suy ra b \(\geq 4.\).
Nếu b = 4 thì \(30\times c+4\times d=298\), suy ra c = 9 và d = 7. (loại vì d phải khác a)
Nếu b = 5 thì \(30\times c+4\times d=98\), suy ra c = 3 và d = 2.
Đáp số: \({\overline{{a b c d}}}=7532\,.\)
Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Chuyên Amsterdam năm học 2013 - 2014.
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS HÀ NỘI AMSTERDAM để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.
Lưu ý: Các em cần Tạo Tài khoản và Đăng Nhập để có thể xem được những nội dung này.