
Để giúp các em học sinh chuẩn bị tốt cho kỳ thi tuyển sinh vào lớp 6 Trường Chuyên Amsterdam, Thầy/cô MATHX biên soạn gửi đến các em giải chi tiết đề thi tuyển sinh vào 6 môn Toán Chuyên Amsterdam 2009 - 2010. Hy vọng rằng tài liệu giải chi tiết này sẽ là công cụ hữu ích, giúp các em nắm bắt được cấu trúc của đề thi, rèn luyện kỹ năng giải bài một cách linh hoạt và chủ động. Chúc các em học sinh có những kết quả xuất sắc trong kỳ thi sắp tới và đạt được vé vào cổng trường mong muốn.
Phụ huynh và các em học sinh xem thêm danh sách đáp án đề thi vào 6 Amsterdam qua các năm tại đây:
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2005 2006
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2006 2007
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2007 2008
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2008 2009
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2009 2010
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2010 2011
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2011 2012
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2012 2013
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2013 2014
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2014 2015
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2019 - 2020
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2020 - 2021
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2022 - 2023
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2023 - 2024
Môn: Toán
Năm học: 2009 - 2010
Bài 1: Tính: \(1{\dfrac{1}{3}}\times1{\dfrac{1}{8}}\times1{\dfrac{1}{15}}\times1{\dfrac{1}{24}}\times...\times1{\dfrac{1}{99}}\)
Hướng dẫn:
\(1{\dfrac{1}{3}}\times1{\dfrac{1}{8}}\times1{\dfrac{1}{15}}\times1{\dfrac{1}{24}}\times...\times1{\dfrac{1}{99}}\)
\(={\dfrac{4}{3}}\times{\dfrac{9}{8}}\times{\dfrac{16}{15}}\times{\dfrac{25}{24}}\times...\times{\dfrac{100}{99}}\)
\(={\dfrac{2\times2}{3}}\times{\dfrac{3\times3}{8}}\times{\dfrac{4\times4}{15}}\times\ldots\times{\dfrac{10\times10}{99}}\)
\(={\dfrac{2\times2}{3}}\times{\dfrac{3\times3}{4\times2}}\times{\dfrac{4\times4}{5\times3}}\times\ldots\times{\dfrac{10\times10}{9\times11}}\)
\(={\dfrac{2\times2\times3\times4\times4\times10\times10}{3\times2\times4\times5\times...\times \ 10 \times11}}\)
\(={\dfrac{2\times10}{11}}={\dfrac{20}{11}}\)
Đáp số: \(\dfrac{20}{11}\).
Bài 2: Tìm số \(\overline {abc}\) biết \(\overline {abc}\) x 5 = \(\overline {dad}\)
Hướng dẫn:
\({\overline{{a b c}}}\times5={\overline{{d a d}}}\) => d = 0 hoặc d = 5, d = 0 (loại) vì d đứng đầu nên d phải khác 0.
\({\overline{{a b c}}}\times5={\overline{{5a5}}}\) = 505 + 10a (chia cả 2 vế cho 5)
\(\overline{{{a b c}}}\,=\,101+2a\lt 200\;\;=\gt a=1\)
=> \({\overline{{a b c}}}=~101+2\times1=103\)
Đáp số: \(\overline {abc}\) = 103
Bài 3: Có ba vòi nước chảy vào một cái bể cạn. Nếu vòi 1 và vòi 2 cùng chảy thì đầy bể sau 1 giờ 12 phút ; nếu vòi 2 và vòi 3 cùng chảy thì đầy bể sau 2 giờ; nếu vòi 3 và vòi 1 cùng chảy thì đầy bể sau 1 giờ 30 phút. Hỏi vòi ba chảy riêng thì đầy bể sau bao lâu ?
Hướng dẫn:
Đổi 1 giờ 12 phút = \(\dfrac{6}{5}\) giờ; 1 giờ 30 phút = \(\dfrac{3}{2}\) giờ
Trong 1 giờ:
Vòi 1 và vòi 2 chảy được:
1 : \(\dfrac{6}{5}\) = \(\dfrac{5}{6}\) (bể)
Vòi 2 và vòi 3 chảy được:
1 : 2 = \(\dfrac{1}{2}\) (bể)
Vòi 3 và vòi 1 chảy được:
1 : \(\dfrac{3}{2}\) = \(\dfrac{2}{3}\) (bể)
Trong 1 giờ vòi 3 chảy được:
(\(\dfrac{1}{2}\) + \(\dfrac{2}{3}\) - \(\dfrac{6}{5}\)) : 2 = \(\dfrac{1}{6}\) (bể)
Thời gian để vòi 3 chảy riêng đầy bể là:
1 : \(\dfrac{1}{6}\) = 6 (giờ)
Đáp số: 6 giờ.
Bài 4: Tổng của các số tự nhiên liên tiếp từ 1 đến n là một số có ba chữ số giống nhau. Tìm số n ?
Hướng dẫn:
Tổng từ 1 đến n là 1 số có 3 chữ số giống nhau: \(\overline {aaa}\)
1 + 2 + 3 + 4 + ... + n = \(\overline {aaa}\)
\({\dfrac{n\times(n+1)}{2}}={\dfrac{\overline{{aaa}}{}}{}}=111\times a=37\times3\times a\)
n x (n + 1) = 37 x 3 x a x 2 = 37 x (6 x a)
Tới đây, chúng ta sẽ có 2 trường hợp:
+) Trường hợp 1:
n = 37 => 6 x a = 37 + 1 = 38 (loại vì 38 không chia hết cho 6)
+) Trường hợp 2:
n + 1 = 37 => 6 x a = n = 37 - 1 = 36 => a = 36 + 6 = 6 (thỏa mãn)
Đáp số: n = 36 và tổng = 666.
Bài 5: Nếu lấy \(\dfrac {3}{5}\) số bông hoa của An chia đều cho Bình, Châu và Duyên thì số bông hoa của 4 bạn bằng nhau. Nếu bớt của An 6 bông hoa thì số bông hoa còn lại của An bằng tổng số bông hoa của ba bạn kia. Hỏi lúc đầu An có bao nhiêu bông hoa ?
Hướng dẫn:
Gọi ban đầu An có a (bông hoa) và mỗi bạn Bình, Châu và Duyên có b (bông hoa)
Lấy \(\dfrac {3}{5}\) số hoa của An chia đều cho 3 bạn thì mỗi bạn có số hoa là:
\(b+{\dfrac{3}{5}}a:3=b+{\dfrac{1}{5}}a\) (bông hoa)
Số hoa còn lại của An là:
\(\dfrac {2}{5}\) x a (bông hoa)
Sau khi cho đi số hoa của 4 bạn như nhau nên:
\(b+{\dfrac{1}{5}}a={\dfrac{2}{5}}a\ =3\ ={\dfrac{2}{5}}a-{\dfrac{1}{5}}a={\dfrac{1}{5}}a\) hay a = 5 x b (bông hoa)
Nếu bớt số hoa của An đi 6 bông thì bằng tổng số hoa của 3 bạn còn lại nên
\(a-6=3\times b=3\times{\dfrac{1}{5}}a={\dfrac{3}{5}}a\)
=> \(a-{\dfrac{3}{5}}a=6\)
=> \({\dfrac{2}{5}}a=6=5a={\dfrac{6\times5}{2}}=15\) (bông hoa)
Đáp số: 15 bông hoa.
Bài 6: Hiện nay tuổi anh gấp 1,5 lần tuổi em và tuổi mẹ gấp đôi tổng số tuổi của hai anh em. Sau 5 năm, tuổi mẹ gấp 1,5 lần tổng số tuổi của hai anh em. Tính tuổi của em hiện nay ?
Hướng dẫn:
Ta có 1,5 = \(\dfrac {3}{2}\)
Nếu coi tuổi em hiện nay là 4 phần. Thì:
Số phần tuổi anh hiện nay là:
4 x \(\dfrac {3}{5}\) = 6 (phần)
Số phần tuổi mẹ hiện nay là:
(4 + 6) x 2 = 20 (phần)
Sau 5 năm tuổi mẹ tăng 5 tuổi, tổng số tuổi của hai anh em tăng lên 5 x 2 = 10 tuổi.
khi đó tuổi mẹ gấp 1,5 lần tổng số tuổi hai anh em. Do vậy, 5 phần bằng 10 tuổi.
Tuổi em hiện nay là:
10 : 5 x 4 = 8 (tuổi)
Đáp số: 8 tuổi.
Bài 7: Cho hình vuông ABCD biết AM = MB = BN = NC = CE = ED = DF = FA = 1cm. Tính diện tích phần có gạch chéo. (Xem hình vẽ)
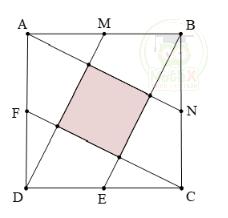
Hướng dẫn:
\(S_{A B B^{\prime}}=\ S_{B C C^{\prime}}=\ S_{C D D^{\prime}}=\ S_{D A A^{\prime}}=\dfrac{AA^{\prime}\times BB^{\prime}}{2}=A^{\prime B^{\prime}}\times B^{\prime}C^{\prime}=\ S_{A {\prime}B{\prime} C{\prime} D{\prime}}\)
+) Diện tích 4 tam giác trên bằng nhau vì có chiều cao và đáy bằng nhau.
+) AB' = 2 x A'B' nên AA' = A'B' = \(\dfrac {AB'}{2}\)
Tương tự: BB' = B'C' = \(\dfrac {BC'}{2}\)
Mà:
\(S_{A B C D}=\ S_{A B B^{\prime}}+\ S_{B C C^{\prime}}+\ S_{C D D^{\prime}}+\ S_{D A A^{\prime}}+\ S_{A^{\prime}B^{\prime}C^{\prime}D^{\prime}}\)
=> \(S_{A B C D}=5\times S_{A^{\prime}B^{\prime}C^{\prime}D^{\prime}}=A B\times B C=4\ \mathrm{}(c m^{2})\)
\(S_{A' B'C'D'}=\dfrac{4}{5}=0,8 \ (c m^{2})\)
Đáp số: 0,8 \(c m^2\)
Bài 8: Một ô tô đi từ A đến C gồm đoạn đường bằng AB và đoạn đường dốc BC, sau đó từ C lại quay về A mất tất cả 7 giờ. Biết vận tốc trên đoạn đường bằng là 40 km/h, xuống dốc là 60km/h, lên dốc là 20 km/h và quãng đường AB bằng quãng đường BC. Tính độ dài quãng đường AC ?
Hướng dẫn:
Tỉ số vận tốc khi ô tô lên dốc và đoạn đường bằng là:
20 : 40 = \(\dfrac {1}{2}\)
Do quãng đường lên dốc và đoạn đường bằng là bằng nhau nên thời gian ô tô đi trên đoạn đường bằng bằng 1/2 thời gian ô tô đi lên dốc.
Tỉ số vận tốc khi ô tô lên dốc và xuống dốc là:
20 : 60 = \(\dfrac {1}{3}\)
Nên thời gian ô tô xuống dốc bằng 1/3 thời gian ô tô lên dốc.
Phân số chỉ 7 giờ bẳng:
1 + \(\dfrac {1}{2}\) + \(\dfrac {1}{2}\)+ \(\dfrac {1}{3}\) = \(\dfrac {7}{3}\) thời gian lên dốc.
Thời gian ô tô lên dốc là:
7 : \(\dfrac {7}{3}\) = (3 giờ)
Đoạn đường BC dài là:
20 x 3 = 60 (km)
Độ dài quãng đường AC là:
60 + 60 = 120 (km)
Đáp số: 120 km.
Bài 9: Tính thể tích hình hộp chữ nhật có chiều dài 5dm, biết rằng nếu chiều dài giảm đi 2dm thì thể tích hình hộp đó giảm đi 12dm3 ?
Hướng dẫn:
Gọi chiều rộng, chiều cao của hinh hộp chữ nhật lần lượt là a (dm), b (dm).
Thể tích hình hộp chữ nhật đó là:
5 x a x b (\(dm^3 \))
Các cạnh của hình hộp chữ nhật mới là: a dm,b dm và 5 - 2 = 3 (dm)
Thể tích là: 3 x a x b (\(dm^3 \))
Ta có: 5 x a x b - 3 x a x b = 12 => 2 x a x b = 12 => a x b = 6.
Thể tích của hình hộp chữ nhật là: 5 x 6 = 30 (\(dm^3 \))
Đáp số: 30 \(dm^3 \).
Bài 10: Học kì I số học sinh nam lớp 5A chiếm 47,5% số học sinh cả lớp. Học kì II, lớp có thêm bốn học sinh nam và hai học sinh nữ nên số học sinh nam chiếm 50% số học sinh cả lớp. Hỏi học kì II lớp 5A có bao nhiêu học sinh ?
Hướng dẫn:
Phân số chỉ số học sinh nữ lớp 5A ở học kỳ I là:
100% - 47,5% = 52,5% (số học sinh cả lớp ở học kỳ I)
Học kỳ II, số nam chiếm 50% số học sinh cả lớp nên học kỳ II số học sinh nam bằng số học sinh nữ, điều này có được vì thêm 4 học sinh nam và 2 học sinh nữ. Như vậy, học kỳ I số học sinh nữ nhiều hơn số học sinh nam là:
4 - 2 = 2 (học sinh)
Phân số chỉ 2 học sinh bằng:
52,5% - 47,5% = 5 % (số học sinh cả lớp kỳ II)
Số học sinh lớp 5A học kì I có là:
2 : 5% = 40 (học sinh)
Số học sinh lớp 5A học kì II có là:
40 + 4 + 2 = 46 (học sinh)
Đáp số: 46 học sinh.
Bài 1: Một con sói đuổi bắt một con thỏ cách xa nó 17 bước của sói. Con thỏ ở cách hang của nó 80 bước của thỏ. Biết rằng khi sói chạy được 1 bước thì thỏ chạy được 3 bước và 1 bước của sói bằng 8 bước của thỏ. Hỏi thỏ có kịp chạy về hang của nó không ? Giải thích tại sao ?
Hướng dẫn:
Để tính xem sói có đuổi được thỏ hay không thì các em phải biết con vật nào sẽ đến cửa hang của thỏ trước:
+) Nếu sói đến trước thì sói sẽ bắt được thỏ.
+) Nếu thỏ đến trước thì sói sẽ không bắt được thỏ.
Chú ý: Nên đổi số bước thỏ hoặc só bước sói về chung một loại, hướng dẫn dưới đây sẽ để là bước thỏ vì bước thỏ nhỏ hơn bước sói tránh phải thực hiện với số thập phân.
Vì 1 bước sói = 8 bước thỏ nên 80 bước thỏ = 80 : 8 = 10 bước sói
Tổng số bước đề sói đến cửa hang của thỏ là:
10 + 17 = 27 (bước sói)
Đổi 27 bước sói = 27 x 3 (bước thỏ) = 81 (bước thỏ).
Vậy sói phải chạy 81 bước thỏ thì mới tới của hàng, còn thỏ chỉ chạy 80 bước.
Đáp số: Sói không bắt được thỏ.
Bài 2: Cùng một lúc người thứ nhất đi từ A đến B và người thứ hai đi từ B về A, hai người gặp nhau tại C cách A một đoạn 4km. Sau đó người thứ nhất đi đến B rồi quay lại A, người thứ hai đi đến A rồi quay ngay về B, hai người gặp nhau lần thứ hai tại D cách B một đoạn 3km. Tính độ dài quãng đường AB ?
Hướng dẫn:
Ta có sơ đồ sau:

Khi gặp nhau lần thứ hai thì tổng quãng đường hai người đi được bằng 3 lần quãng đường AB. Hai người gặp nhau lần đầu tại C cách A 4 km hay nói cách khác khi đó người thứ nhất đã đi được 4 km. Vậy cứ mỗi lần hai người đi được tổng quảng đường là
AB thì người thứ nhất đi được 4 km.
Vậy:
Đến khi gặp nhau lần 2 thì người thứ nhất đi được:
3 x 4 = 12 (km)
Quãng đường người thứ nhất đi được bằng quãng đường AB cộng thêm 3 km.
Quãng đường AB là:
12 - 3 = 9 (km)
Đáp số: 9 km.
Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Chuyên Amsterdam năm học 2009 - 2010.
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS HÀ NỘI AMSTERDAM để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.
Lưu ý: Các em cần Tạo Tài khoản và Đăng Nhập để có thể xem được những nội dung này.