
Để giúp các em học sinh chuẩn bị tốt cho kỳ thi tuyển sinh vào lớp 6 Trường Chuyên Amsterdam, Thầy/cô MATHX biên soạn gửi đến các em giải chi tiết đề thi tuyển sinh vào 6 môn Toán Chuyên Amsterdam 2007 - 2008. Hy vọng rằng tài liệu giải chi tiết này sẽ là công cụ hữu ích, giúp các em nắm bắt được cấu trúc của đề thi, rèn luyện kỹ năng giải bài một cách linh hoạt và chủ động. Chúc các em học sinh có những kết quả xuất sắc trong kỳ thi sắp tới và đạt được vé vào cổng trường mong muốn.
Phụ huynh và các em học sinh xem thêm danh sách đáp án đề thi vào 6 Amsterdam qua các năm tại đây:
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2005 2006
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2006 2007
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2007 2008
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2008 2009
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2009 2010
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2010 2011
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2011 2012
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2012 2013
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2013 2014
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2014 2015
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2019 - 2020
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2020 - 2021
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2022 - 2023
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2023 - 2024
Môn: Toán
Năm học: 2007 - 2008
Bài 1. Tính: \(\left(1-{\dfrac{1}{4}}\right)\times\left(1-{\dfrac{1}{9}}\right)\times\left(1-{\dfrac{1}{16}}\right)\times\left(1-{\dfrac{1}{25}}\right)\times\left(1-{\dfrac{1}{36}}\right) \ ?\)
Hướng dẫn:
\(\left(1-{\dfrac{1}{4}}\right)\times\left(1-{\dfrac{1}{9}}\right)\times\left(1-{\dfrac{1}{16}}\right)\times\left(1-{\dfrac{1}{25}}\right)\times\left(1-{\dfrac{1}{36}}\right) \ ?\)
\(={\dfrac{3}{4}}\times{\dfrac{8}{9}}\times{\dfrac{15}{16}}\times{\dfrac{24}{25}}\times{\dfrac{35}{36}}={\dfrac{3\times8\times5\times3\times6\times4\times7\times5}{4\times3\times3\times8\times2\times5\times5\times6\times6}}={\dfrac{7}{12}}\)
Đáp số: \(\dfrac{7}{12}\).
Bài 2. Tìm x biết: ( x + 4) + ( x + 6) + ( x + 8) + .....+ ( x + 26) = 210 ?
Hướng dẫn:
(x + 4) + (x + 6) + (x + 8) + ...+ (x + 26) = 210
12 x + (4 + 6 + ... + 26) = 210
12 × x + (4 + 26) × 12 : 2 = 210
12 × x + 180 = 210
12 × x = 30
x = 30 : 12
x = 2,5
Đáp số: 2,5.
Bài 3. Tìm một số tự nhiên có chữ số hàng đơn vị là 7 và khi xoá chữ số 7 đó thì được một số mới kém số đã cho 295 đơn vị ?
Hướng dẫn:
Xóa chữ số 7 ở hàng đơn vị của một số tức là bớt số đó đi 7, rồi giảm đi 10 lần.
Sau khi xóa chữ số 7 ở hàng đơn vị thì số đó trở thành số:
(295 - 7) : (10 - 1) = 32
Số tự nhiên cần phải tìm là 327.
Đáp số: 327.
Bài 4. Hiện nay tuổi mẹ gấp 3 lần tuổi con. Sau 4 năm nữa tuổi mẹ gấp 2,5 lần tuổi con. Tính tuổi con hiện nay ?
Hướng dẫn:
Hiện nay, tuổi mẹ hơn tuổi con:
3 - 1 = 2 (lần tuổi con hiện nay)
Sau 4 năm nữa tuổi mẹ hơn tuổi con:
2,5 - 1 = 1,5 (lần tuổi con sau 4 năm)
Vì tuổi mẹ hơn tuổi con không đổi theo thời gian.
Do vậy: 2 - 1,5 = 0,5 (lần tuổi con hiện nay) bằng: 4 x 1,5 = 6 (tuổi)
Tuổi con hiện nay là:
6 : 0,5 = 12 tuổi.
Đáp số: 12 tuổi
Bài 5. Tìm các chữ số a, b khác 0 thoả mãn: \(a\times b\times{\overline{{a b}}}={\overline{{b bb}}} \ ?\)
Hướng dẫn:
\(a\times b\times \overline{ab}=\,{\overline{{b}}}{\overline{{b}}}{\overline{{b}}}\)
\(a\times b\times{\overline{{a b}}}=~b\times111\)
\(a\times{\overline{{a b}}}=\ 111=3\times37\)
Vậy a = 3 và b = 7.
Đáp số: a = 3; b = 7
Bài 6. Bạn Bắc dùng các khối lập phương nhỏ cạnh 1dm xếp thành khối lập phương lớn có thể tích 64\(dm^3\). Sau đó bạn lấy ra 4 khối lập phương nhỏ ở 4 đỉnh phía trên của khối lập phương lớn. Tính diện tích toàn phần của khối còn lại ?
Hướng dẫn:
Thể tích = 64 = cạnh x cạnh x cạnh = 4 x 4 x 4
Cạnh của khối lập phương lớn là 4 dm. Diện tích toàn phần của khối lập phương lớn nhà:
4 x 4 x 6 = 96 (\(dm^2\))
Lấy ra 4 khối lập phương nhỏ ở 4 đỉnh phía trên của hình lập phương lớn thì diện tích toàn phần không đổi. Vậy diện tích toàn phần của khối còn lại là 96 \(dm^2\).
Đáp số: S = 96 \(dm^2\)
Bài 7. Hình vuông ABCD có cạnh 8cm, AC cắt BD tại O. Vẽ đường tròn tâm O bán kính OA như hình vẽ. Tính diện tích phần gạch chéo ?
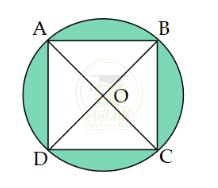
Hướng dẫn:
Diện tích phần tô đậm = diện tích hình tròn - diện tích hình vuông ABCD.
Diện tích hình vuông ABCD là:
\(S_{A B C D}=4\times S_{O A B}=4\times{\frac{OA\times OB}{2}}=2\times O A\times O B=A B\times B C=64\left(cm^{2}\right)\)
=> \(O A\times O B=\,64\div2=32\,(c m^{2})\)
Diện tích hình tròn là:
\(S_{t r ò n}=3,14\) x bán kính x bán kính = 3,14 x OA x OB
Diện tích phần tô đậm là:
\(S_{đậm}=S_{tròn} - S_{ABCD} = 3,14 × OA × OB - 2 × OA × OB\)
\(S_{đậm}\) = 1,14 x OA x OB = 1,14 x 32 = 36,48 (\(cm^2\))
Đáp số: 36,48 \(cm^2\)
Bài 8. Quãng đường từ A đến B gồm một đoạn lên dốc, một đoạn xuống dốc. Một ô tô đi từ A đến B rồi quay về A mất 10 giờ 30 phút. Tính độ dài quãng đường AB, biết vận tốc khi lên dốc là 30km/giờ và khi xuống dốc là 60km/giờ ?
Hướng dẫn:
Đổi 10 giờ 30 phút = \(\dfrac {21} {2}\) giờ
Trên mỗi ki-lô-mét của quãng đường AB thì đều có một lần ô tô đi với vận tốc 30 km/h, một lần ô tô đi với vận tốc 60 km/h.
1 km đi với vận tốc 60 km/h hết:
1 : 60 = \(\dfrac {1} {60}\) (giờ)
1 km đi với vận tốc 30 km/h hết:
1 : 30 = \(\dfrac {1} {30}\) (giờ)
Do đó, 1km cả đi và về hết:
\(\dfrac {1} {30}\) + \(\dfrac {1} {60}\) = \(\dfrac {1} {20}\) (giờ)
Quãng đường AB dài:
\(\dfrac {21} {2}\) : \(\dfrac {1} {20}\) = 210 (km)
Đáp số: 210 km.
Bài 9. 15 công nhân mỗi ngày làm 8 giờ thì hoàn thành công việc được giao trong 20 ngày. Hỏi nếu thêm 5 công nhân và mỗi ngày làm 10 giờ sẽ hoàn thành công việc đó sau bao nhiêu ngày?
Hướng dẫn:
Số giờ 15 công nhân làm trong 20 ngày là:
8 x 20 = 160 (giờ)
1 công nhân làm xong công viêc đó phải hết:
160 x 15 = 2400 (giờ)
20 công nhân làm xong công việc đó phải hết:
2400 : 20 = 120 (giờ)
Mỗi ngày làm 10 giờ thì số ngày hoàn thành công việc là:
120 : 10 = 12 (ngày)
Đáp số: 12 ngày.
Bài 10. Trong một tháng có 3 ngày thứ 7 là ngày chẵn. Hỏi ngày 13 của tháng đó là thứ mấy?
Hướng dẫn:
Ngày 2 phải là ngày thứ 7 đầu tiên, vì nếu ngày 4 là thứ bảy đầu tiên thì ngày thứ bảy lần thứ 3 là ngày chẵn sẽ không thuộc vào tháng này.
Vậy các ngày thứ 7 là ngày chẵn của tháng này là: 2; 16; 30.
Do đó, ngày 13 của tháng đó là ngày thứ 4.
Đáp số: Thứ 4
Bài 1. Bốn bạn Xuân, Hạ, Thu, Đông chơi đấu cờ, mỗi bạn thi đấu 1 ván với từng người còn lại. Mỗi ván thắng được 1 điểm, hoà 0,5 điểm và thua 0 điểm. Biết trong các ván cờ có 3 ván hoà, Hạ được 1,5 điểm, Thu và Đông mỗi người được 1 điểm. Hãy tính số điểm của Xuân và cho biết kết quả ván cờ giữa Xuân và Hạ ?
Hướng dẫn:
Mỗi bạn đấu với 3 bạn còn lại 3 ván đấu.
Có 4 bạn nên số ván đấu là:
3 x 4 = 12 (ván)
Tuy nhiên mỗi ván đấu được tính 2 lần.
Số ván đấu thực sự có là:
12 : 2 = 6 (ván)
Tổng số điển cả 4 bạn đạt được là:
1 x 6 = 6 điểm
Số điểm của Xuân là:
6 - (1,5 + 1 + 1) = 2,5 (điểm)
Do vậy Xuân thắng 2 ván hòa 1 ván.
Nếu Xuân sẽ thắng hoặc hòa với Hạ.
Nếu Xuân hòa Hạ khi đấu với Thu và Đông sẽ có 2 ván hóa, hoặc 1 thắng 1 hòa. Cả hai trường hợp này đều không có 3 ván hòa. Do vậy không xảy ra trường hợp Xuân hòa Hạ.
Vậy kết quả ván cờ giữa Xuân và Hạ thì Xuân thắng.
Đáp số: Xuân thắng.
Bài 2. Có 3 hộp giống hệt nhau, một hộp đựng 2 bóng đỏ, một hộp đựng 2 bóng xanh, một hộp đựng 1 bóng đỏ và 1 bóng xanh được dán nhãn theo màu bóng ĐĐ, XX, ĐX. Nhưng do dán nhầm nên các nhãn đều khác màu bóng trong hộp. Làm thế nào chỉ cần lấy ra 1 quả mà biết được màu bóng trong cả 3 hộp ?
Hướng dẫn:
Lấy 1 quả trong hộp dán nhãn ĐX xảy ra hai trường hợp.
TH1: Nếu quả lấy ra là bóng xanh thì hộp ĐX đựng hai quả bóng xanh, hộp ĐĐ không đựng 2 quả bóng xanh, không đựng 2 quả bóng đỏ. Vậy hộp ĐĐ đựng 1 quả bóng xanh 1 quả bóng đỏ. Còn lại hộp XX sẽ đựng 2 quả bóng đỏ.
TH2: Nếu quả lấy ra là quả bóng đỏ thì hộp ĐX đựng 2 quả bóng đỏ, hộp XX không đựng 2 quả bóng xanh, không đựng hai quả bóng đỏ. Vậy XX đựng 1 quả bóng xanh và 1 quả bóng đỏ. Còn lại hộp ĐĐ sẽ đựng 2 quả bóng xanh.
Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Chuyên Amsterdam năm học 2007 - 2008.
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS HÀ NỘI AMSTERDAM để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.
Lưu ý: Các em cần Tạo Tài khoản và Đăng Nhập để có thể xem được những nội dung này.