
Để giúp các em học sinh chuẩn bị tốt cho kỳ thi tuyển sinh vào lớp 6 Trường Chuyên Amsterdam, Thầy/cô MATHX biên soạn gửi đến phụ huynh và các em hướng dẫn giải chi tiết các dạng bài trong đề thi lên lớp 6 các năm của trường chuyên Hà Nội Amsterdam. Hy vọng rằng tài liệu giải chi tiết này sẽ là công cụ hữu ích, giúp các em nắm bắt được cấu trúc của đề thi, rèn luyện kỹ năng giải bài một cách tốt linh hoạt và chủ động hơn. Chúc các em học sinh có những kết quả xuất sắc trong kỳ thi sắp tới và đạt được vé vào cổng trường mong muốn.
Phụ huynh và các em học sinh xem thêm danh sách đáp án đề thi vào 6 Amsterdam qua các năm tại đây:
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2005 2006
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2006 2007
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2007 2008
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2008 2009
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2009 2010
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2010 2011
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2011 2012
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2012 2013
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2013 2014
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2014 2015
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2019 - 2020
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2020 - 2021
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2022 - 2023
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2023 - 2024
Môn: Toán
Năm học: 2011 - 2012
Bài 1: Viết số tự nhiên nhỏ nhất có năm chữ số khác nhau sao cho tổng các chữ số của số đó là 23.
Hướng dẫn:
Gọi số có 5 chữ số cần tìm là \(\overline {abcde}\).
Vì đề bài yêu cầu tìm số nhỏ nhất nên a phải càng nhỏ càng tốt, và a là chữ số đầu nên a phải khác 0. Vậy a = 1.
Tương tự b phải là số càng nhỏ càng tốt => b = 0.
Còn lại: c + d + e = 23 - 1 = 22.
Để số cần tìm nhỏ nhất thì số hàng đơn vị và số hàng chục cảng lớn càng tốt. Vậy lựa chọn e = 9 => c + d = 22 - 9 = 13.
d là số lớn nhất khác 9 nên d = 8 => c = 13 - 8 = 5.
Vậy số có 5 chữ số nhỏ nhất có tổng bằng 23 là số: 10589.
Đáp số: 10589.
Bài 2: Tìm ab biết rằng ab = ba × 3 + 6.
Hướng dẫn:
\(a\times10+b=(b\times10+a)\times3+6\)
\(10a+b=30b+3a+6\)
\(10a-3a=30b-b+6=29b+6\)
7a = 29 b + 6
\(7\times(a-4b)=\,b+6\)
Vậy b = 6 phải chia hết cho 7 và a - 4b > 0
=> b = 1 hoặc b = 8 và b < 3 => b = 1.
Khi b = 1 thì: 7 x
\(7\times(a-4)=\ 7\ =\gt a-4=1\ => \ a=5\)
Kết luận: Số phải tìm là 51.
Đáp số: 51.
Bài 3: Giá 11 cái bút bằng giá của 2 quyển vở và 1 quyển sách. Giá của 5 quyển vở bằng giá của 3 quyển sách. Hỏi giá 10 quyển vở và 9 quyển sách bằng giá của bao nhiêu cái bút?
Hướng dẫn:
11 cái bút = 2 quyền vở + 1 quyền sách
33 cái bút = 6 quyền vở + 3 quyền sách (nhân cả 2 về với 3)
Mà giá của 5 quyển vở = 3 quyền sách nên:
33 cái bút = 6 quyền vở + 5 quyền vở = 11 quyền vở.
3 cái bút = 1 quyền vở.
Vì 5 quyển vở = 3 quyền sách => 9 quyền sách = 15 quyển vở.
Vậy 10 quyển vở + 9 quyền sách = 10 quyền vở + 15 quyển vở
= 25 quyền vở
= 25 x 3 cái bút
= 75 cái bút.
Đáp số: 75 cái bút.
Bài 4: Hiện nay tuổi bố bằng tuổi mẹ cộng với tuổi con. Khi tuổi mẹ bằng tuổi bố hiện nay thì tuổi mẹ gấp ba lần tuổi con và tổng số tuổi của ba người lúc đó sẽ là 90. Tính tuổi con hiện nay.
Hướng dẫn:
Gọi tuổi hiện nay là a (tuổi) = > tuổi bố = tuổi mẹ + a (tuổi).
Khi tuổi mẹ bằng tuôi bố hiện tại thì tuổi con là 2a (tuổi), tuổi mẹ gấp 3 lần tuổi con nên tuổi mẹ là 6a (tuổi), tuổi bố = tuổi mẹ + a = 7a (tuổi).
Tổng số tuổi của cả 3 người sẽ là:
2a + 6a + 7a = 90 (tuổi)
15a = 90 (tuổi)
a = 90 : 15 = 6 (tuổi)
Vậy con hiện nay 6 tuổi.
Đáp số: 6 tuổi.
Bài 5: Xếp các hình lập phương nhỏ có cạnh 2 cm thành hình lập phương lớn có thể tích 216 \(cm^3\). Sau đó lấy đi một hình lập phương nhỏ ở chính giữa mặt bên của hình lập phương lớn. Tính diện tích toàn phần của hình còn lại.
Hướng dẫn:
Thể tích hình lập phương lớn = 216 (\(cm^3\)) = 6 x 6 x 6
Vậy cạnh hình lập phương lớn là 6 (cm)
Diện tích toàn phần của hình lập phương là:
6 x 6 x 6 = 216 (\(cm^2\))
Diện tích một mặt của hình lập phương nhỏ là:
2 x 2 = 4 (\(cm^2\))
Khi lấy đi một hình lập phương nhỏ ở chính giữa mặt bên của hình lập phương lớn thì diện tích toàn phần của hình lập phương lớn sẽ tăng lên thêm 4 mặt của hình lập phương nhỏ.
Vậy diện tích toàn phần của hình lập phương lớn là:
216 + 4 x 4 = 216 + 16 = 232 (\(cm^2\))
Đáp số: 232 \(cm^2\)
Bài 6: Nhân ngày quốc tế thiếu nhi, một cửa hàng giảm giá 10% so với giá định bán nhưng vẫn có lãi 12,5% so với tiền vốn. Hỏi nếu không hạ giá thì cửa hàng đó lãi bao nhiêu phần trăm so với tiền vốn?
Hướng dẫn:
Coi giá bán hôm trước là 100% thì giá bán hôm sau là:
100% - 10% = 90%.
Vậy tỉ số của giá bán hôm sau so với giá bán hôm trước là: \(\dfrac{{90\% }}{{100\% }} = \dfrac{9}{{10}} \)
Hôm sau giảm giá bán 10% nhưng vẫn lãi 12,5%. Vậy tổng cả tiền vốn lẫn tiền lãi sẽ là:
100% + 12,5% =`112,5%.
Phần trăm tiền lãi nếu không giảm giá bán sẽ là:
\(112,5\ +{\dfrac{9}{10}}={\dfrac{1125}{9}}=125\) (%)
Vậy nếu không giảm giá, cửa hàng đó sẽ lại 25%.
Đáp số: 25%.
Bài 7: Một người đi từ A đến B bằng xe đạp trong 4 giờ với vận tốc 12 km/giờ, sau đó đi bằng xe máy trong 6 thì đến B. Lúc về, người đó đi bằng xe máy trong 2 giờ rồi đi ô tô trong 3 giờ thì về đến A, biết vận tốc xe máy bằng nửa vận tốc ô tô, tính quãng đường AB.
Hướng dẫn:
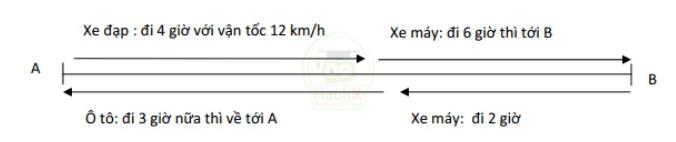
Công thức dùng trong chuyền động đều: Quãng đường = vận tốc x thời gian
Vận tốc và quãng đường là hai đại lượng tỉ lệ thuận.
Vận tốc xe máy bằng nửa vận tốc ô tô nên quãng đường ô tô đi trong 3 giờ bằng xe máy đi trong 6 giờ.
Do quảng đường lúc đi và lúc về là như nhau nên:
\(V_{xe \ đạp}\) x 4 (giờ) + \(V_{xe \ máy}\) x 6 (giờ) = \(V_{xe \ máy}\) x 2 (giờ) + \(V_{xe \ máy}\) x 6 (giờ)
=> \(V_{xe \ đạp}\) x 4 (giờ) + \(V_{xe \ máy}\) x 2 (giờ)
=> \(V_{xe \ máy}\) = 2 x \(V_{xe \ đạp}\) = 2 x 12 = 24 (km/giờ)
Người đó đi từ B đến A mắt 2 + 6 = 8 (giờ) đi xe máy nên quãng đường AB dài là
24 x 8 = 192 (km)
Đáp số: 192 km.
Bài 8: Cho tam giác ABC biết BM = MC, CN = 3NA, và diện tích tam giác AEN bằng 27 cm2. Tính diện tích tam giác ABC.
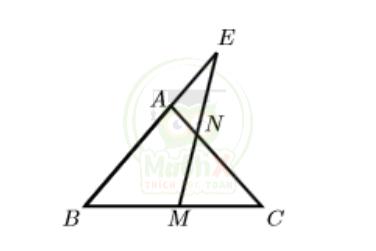
Hướng dẫn:
Do M là trung điểm của BC nên \(S_{BME} =S_{CME}\) (vì cùng chiều cao hạ từ đỉnh C xuống, có cạnh đáy BM = MC)
Tương tự, \(S_{BNE} =S_{CNE}\) = 3 x \(S_{ANE}\) (do CN = 3NA)
Từ đó ta có \(S_{B N A}=\ 2\times S_{A N E}=2\times27=54\left(c m^{2}\right)\)
\(S_{A B C}=\ S_{A B N}+\ S_{B N C}\)
\(\,\,=\,S_{A B N}\,+\,3\times S_{A B N}\)
\(=4\times S_{A B N}=216\left(c m^{2}\right)\)
Đáp số: 216 \(cm^2\)
Bài 9: Tổng của ba số nguyên là 2904. Nếu lấy số thứ nhất chia cho số thứ hai thì được thương là 3 dư 1. Nếu lấy số thứ hai chia cho số thứ ba cũng được thương là 3 dư 1. Tìm số thứ nhất.
Hướng dẫn:
Gọi số thứ ba là a thì:
Số thứ hai sẽ là: 3a + 1
Số thứ nhất sẽ là: 3 x (a x 3 + 1) + 1 = 9a + 4
Tổng của ba số là:
a + 3a + 1 + 9a + 4 = 2904.
13a + 5 = 2904.
13a = 2904 - 5 = 2899.
a = 2899 : 13 = 223.
Số thứ nhất sẽ là: 233 x 9 + 4 = 2011.
Đáp số: 2011.
Bài 10: Tìm x sao cho: \(\left(x+{\dfrac{1}{1\times3}}\right)+\left(x+{\dfrac{1}{3\times5}}\right)+\left(x+{\dfrac{1}{5\times7}}\right)+\cdots+\left(x+{\dfrac{1}{23\times25}}\right)\) \(=11\times x+\left({\dfrac{1}{3}}+{\dfrac{1}{9}}+{\dfrac{1}{27}}+{\dfrac{1}{81}}+{\dfrac{1}{243}}\right)\)
Hướng dẫn:
Số số hạng chứa x là: \({\dfrac{25-3}{2}}+1=12\) số.
\(12\times x+\left({\dfrac{1}{1\times3}}+{\dfrac{1}{3\times5}}+\ldots+{\dfrac{1}{23\times25}}\right)=\mathrm{~11}x+({\dfrac{1}{3}}+{\dfrac{1}{9}}+{\dfrac{1}{27}}+{\dfrac{1}{81}}+{\dfrac{1}{243}})\)
\(12\times x+A=11\times x+B\)
x = B - A
Chúng ta thực hiện tính tổng trước:
\(A=\left({\dfrac{1}{1\times3}}+{\dfrac{1}{3\times5}}+\ldots+{\dfrac{1}{23\times25}}\right)={\dfrac{1}{2}}\times\left({\dfrac{2}{1\times3}}+{\dfrac{2}{3\times5}}+\ldots+{\dfrac{2}{23\times25}}\right)\)
\(={\dfrac{1}{2}}\times(\ 1-{\dfrac{1}{3}}+{\dfrac{1}{3}}-{\dfrac{1}{5}}+{\dfrac{1}{5}}-{\dfrac{1}{7}}+{\dfrac{1}{7}}-{\dfrac{1}{9}}+\dots+{\dfrac{1}{23}}-{\dfrac{1}{25}})\)
\(={\dfrac{1}{2}}\times\left(1-{\dfrac{1}{25}}\right)={\dfrac{1}{2}}\times{\dfrac{24}{25}}={\dfrac{12}{25}}\)
\(B={\dfrac{1}{3}}+{\dfrac{1}{9}}+{\dfrac{1}{27}}+{\dfrac{1}{81}}+{\dfrac{1}{243}}={\dfrac{1}{3}}\times\left(1+{\dfrac{1}{3}}+{\dfrac{1}{9}}+{\dfrac{1}{27}}+{\dfrac{1}{81}}\right)={\dfrac{1}{3}}\times\left(B+1-{\dfrac{1}{243}}\right)\)
\(={\dfrac{1}{3}}B+{\dfrac{242}{3\times243}}\)
Vậy \(B-{\dfrac{1}{3}}B={\dfrac{242}{3\times243}}=\gt {\dfrac{2}{3}}B={\dfrac{242}{3\times243}}=\gt B={\dfrac{121}{243}}\)
\(x=B-A={\frac{121}{243}}-{\dfrac{12}{25}}={\dfrac{3025-2916}{6075}}={\dfrac{109}{6075}}\)
Đáp số: \(x = \dfrac{109}{6075}\)
Bài 1: Một giải bóng đá có bốn đội A,B,C,D tham gia. Mỗi đội đấu với từng đội còn lại một trận. Đội thắng được 3 điểm, thua được 0 điểm, nếu hòa thì mỗi đội được 1 điểm. Kết quả là đội A được 7 điểm, đội B được 5 điểm, đội C được 3 điểm, đội D được 1 điểm. Hỏi có tất cả mấy trận hòa trong giải bóng đá và trận đấu giữa đội A và đội C có kết quả thế nào?
Hướng dẫn:
Tổng điêm của 4 đội là 16 điểm. Tông số trận đầu là 6 trận.
Tổng điểm của hai đội trong mỗi trận thắng - thua là 3 điểm, trong mỗi trận hòa là 2 điểm.
Nếu không có trận nào hòa thì tông điểm của 4 đội phải là 6 x 3 = 18 điểm. mà tổng số điểm thực có của 4 đội là 16 điểm nên suy ra có 18 - 16 = 2 trận hòa.
Đội A đấu 3 trận được tổng số điểm là 7 điểm, suy ra đội A không thua trận nào.
Đội C đấu 3 trận được tổng số điểm là 3 điểm, mà chỉ có tất cả 2 trận hòa nên đội C thua 2 trận và thắng 1 trận, suy ra đội C thua đội A.
Vậy có 2 trận hòa và đội A thắng đội C.
Bài 2: Cho bốn số tự nhiên bất kỳ a,b,c,d và a > b > c > d. Chứng tỏ rằng tích của tất cả các số tự nhiên là hiệu của hai trong bốn số đã cho là một số chia hết cho 12.
Hướng dẫn:
Ta cần chứng minh rằng: p = (a − b) (a − c)(a − d) (b − c) (b − d) (c − d) chia hết cho 12.
Nhận xét rằng khi chia một số cho 3 thì số dư là một trong ba số 0, 1, 2. Xét tính chia hết của p với 3 và 4, riêng rẽ. Theo nguyên lý Dirichlet, tồn tại ít nhất hai số nguyên trong bốn số a, b, c, d cho cùng số dư khi chia cho 3.
Hiệu của những hai số này chia hết cho 3. Do đó, p chia hết cho 3. Nếu tồn tại hai trong bốn số nguyên a,b,c,d cho cùng số dư khi chia cho 4, thì p chia hết cho 4, theo cách lập luận như trên.
Nếu không, các số dư của a, b, c, d khi chia cho 4 sẽ khác nhau. Nhưng khi đó, hai trong bốn số cùng tính chẵn lẻ, cặp còn lại cũng cùng tính chẵn lẻ, thì hiệu của chúng đều chẵn. Tích của hai số chẵn chia hết cho 4. Do đó, p chia hết cho 4. Vậy, p chia hết cho 12.
Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Chuyên Amsterdam năm học 2011 - 2012.
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS HÀ NỘI AMSTERDAM để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.
Lưu ý: Các em cần Tạo Tài khoản và Đăng Nhập để có thể xem được những nội dung này.