
Để giúp các em học sinh chuẩn bị tốt cho kỳ thi tuyển sinh vào lớp 6 Trường Chuyên Amsterdam, Thầy/cô MATHX biên soạn gửi đến phụ huynh và các em hướng dẫn giải chi tiết các dạng bài trong đề thi lên lớp 6 các năm của trường chuyên Hà Nội Amsterdam. Hy vọng rằng tài liệu giải chi tiết này sẽ là công cụ hữu ích, giúp các em nắm bắt được cấu trúc của đề thi, rèn luyện kỹ năng giải bài một cách tốt linh hoạt và chủ động hơn. Chúc các em học sinh có những kết quả xuất sắc trong kỳ thi sắp tới và đạt được vé vào cổng trường mong muốn.
Phụ huynh và các em học sinh xem thêm danh sách đáp án đề thi vào 6 Amsterdam qua các năm tại đây:
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2005 2006
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2006 2007
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2007 2008
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2008 2009
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2009 2010
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2010 2011
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2011 2012
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2012 2013
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2013 2014
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2014 2015
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2019 - 2020
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2020 - 2021
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2022 - 2023
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2023 - 2024
Môn: Toán
Năm học: 2014 - 2015
Bài 1: Tính: \(S={\dfrac{1}{5\times 9}}+{\dfrac{1}{9\times13}}+{\dfrac{1}{13\times17}}+\ldots+{\dfrac{1}{41\times45}}\ \)
Hướng dẫn:
\(S={\dfrac{1}{4}}\times({\dfrac{4}{5\times9}}+{\dfrac{4}{9\times13}}+{\dfrac{4}{13\times17}}+...+{\dfrac{4}{41\times45}})\)
\(S={\dfrac{1}{4}}\times({\dfrac{1}{5}}-{\dfrac{1}{9}}+{\dfrac{1}{9}}-{\dfrac{1}{13}}+{\dfrac{1}{13}}-{\dfrac{1}{17}}+\ldots+{\dfrac{1}{41}}-{\dfrac{1}{45}})\)
\(S={\dfrac{1}{4}}\times({\dfrac{1}{5}}-{\dfrac{1}{45}})\)
\(S={\dfrac{1}{4}}\times\left({\dfrac{9-1}{45}}\right)\)
\(S={\dfrac{2}{45}}\)
Đáp số: \(\dfrac{2}{45}\)
Bài 2: Một đoàn tàu đánh cá có 45 chiếc tàu, gồm 2 loại: Loại tàu nhỏ thì mỗi tàu có 15 ngư dân làm việc và loại tàu lớn mỗi tàu có 18 ngư dân làm việc. Tổng cộng số ngư dân trên 45 chiếc tàu là 789 người. Hỏi có bao nhiêu tàu lớn ?
Hướng dẫn:
Giải sử tất cả các tàu đều là tàu lớn, vậy số ngư dân trên tàu tất cả là:
45 x 18 = 810 (Ngư dân)
Số ngư dân thừa ra so với đề bài là:
810 - 789 = 21 (Ngư dân)
Khi thay mỗi tàu lớn bằng 1 tàu bé,số ngư dân tổng giảm đi là:
18 - 15 = 3 (Ngư dân)
Số tàu bé cần để thay là
21 : 3 = 7 (tàu)
Số tàu lớn cần là
45 - 7 = 38 (tàu)
Đáp số: 38 tàu lớn.
Bài 3: Một hình hộp chữ nhật có số đo chiều rộng, chiều dài, chiều cao (đơn vị tính là dm) theo thứ tự đó là ba số đo tự nhiên liên tiếp tăng dần. Nếu giảm số đo chiều cao đi 2dm thì diện tích xung quanh của hình hộp chữ nhật mới bằng 60 % diện tích xung quanh của hình hộp chữ nhật ban đầu. Tính thể tích của hình hộp chữ nhật ban đầu ?
Hướng dẫn:
Gọi chiều rộng hình hộp chữ nhật có độ dài là a (dm) thì
Chiều dài là (a + 1 ) (dm) và chiều cao là (a + 2) (dm).
Ban đầu diện tích xung quanh hình hộp chữ nhật là:
\(S_{xq}\) = chu vi đáy x chiều cao
\(S_{xq1}\) = (a + a + 1) x 2 x (a + 2) = 2 x (2 x a + 1) x (2 +a)
Sau khi giảm chiều cao thì điện tích xung quanh của hình hộp chữ nhật là
\(S_{xq2}\) = (a + a + 1) x 2 x a = 2 x (2 x a + 1) x a
Vì diện tích xung quanh mới bằng 60% diện tích xung quanh ban đầu nên
\({\frac{S_{x q1}}{S_{x q2}}}={\dfrac{60}{100}}\) hay \({\dfrac{a}{a+2}}={\dfrac{3}{5}}\)
Vậy a = 3 (dm)
Thể tích hình hộp chữ nhật ban đầu là
Thể tích = dài x rộng x cao = 3 x 4 x 5 = 60 (\(dm^3\))
Đáp số: 60 \(dm^3\)
Bài 4: Một bà mẹ có một con gái và một con trai. Năm nay mẹ 32 tuổi, con gái 6 tuổi và con trai 2 tuổi. Sau bao nhiêu năm nữa thì số tuổi của mẹ gấp rưỡi tổng số tuổi của cả hai con ?
Hướng dẫn:
Tuổi mẹ hiện tại là 32 (tuổi)
Tổng số tuổi của 2 con hiện tại là 6 + 2 = 8 (tuổi)
Vậy cứ sau một năm mẹ tăng thêm 1 tuổi thì tổng số tuổi của hai con lại tăng lên 2 tuổi.
Gọi n là số năm sau để tuổi mẹ gắp rười tổng số tuôi của 2 con. Tức là nếu mẹ tăng thêm n (tuổi) thì tổng số tuổi 2 con sẽ tăng thêm 2 x n (tuổi).
Tuổi của mẹ sau n (năm) là:
32 + n (tuổi)
Tổng số tuổi của 2 con sau n (năm) là:
8 + 2 x n (tuổi)
Vì tuổi mẹ gấp rưỡi tổng số tuổi của 2 con nên:
32 + n = (8 + 2 x n) x 1,5
32 + n = 12 + 3 x n
32 - 12 = 3 x n - n
20 = 2 x n
= 20 + 2 = 10
Vậy sau 10 năm nữa mẹ 42 tuổi và tổng số tuôi của 2 con là 8 + 20 = 28 tuổi
42 : 28 = 1,5 thỏa mãn đầu bài.
Đáp số: Sau 10 năm.
Bài 5: Cho bốn hình tròn, mỗi hình tròn được chia thành 5 phần (như hình vẽ) Người ta điền các số tự nhiên 5, 6, 7, ...., 19, 20 vào mỗi phần trên sao cho hai phần khác nhau được điền hai số khác nhau.Biết rằng tổng các số điền trong các phần của mỗi hình tròn bằng 60. Tính tổng bốn số được điền ở bốn kí hiệu A; B; C; D ?
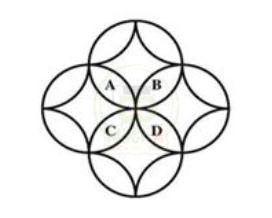
Hướng dẫn:
Tách riêng 4 hình tròn ra thì tổng của chúng sẽ là:
60 x 4 = 240
Tuy nhiên đề bài chỉ điền từ số 5 đến số 20 nên tổng thực tế điền vào các ô sẽ là:
5 + 6 + 7 + ... + 20 = A
Số số hạng = \({\dfrac{(20-5)}{1}}+1=16\) (số)
Tổng A = \({\dfrac{(5+20)\times16}{2}}=200\)
Kết hợp 4 hình tròn lại với nhau tổng dư ra chính là tổng các ô A,B,C,D nên tổng các ô A,B,C,D là:
240 - 200 = 40
Đáp số: 40
Bài 6: Một ô tô đi từ A đến B với vận tốc dự định và trong một thời gian dự định. Sau khi đi được 1 giờ thì ô tô giảm vận tốc chỉ còn bằng 80% vận tốc ban đầu nên đến B chậm 1 giờ so với dự định. Nếu từ A sau khi đi được 1 giờ, ô tô lại đi thêm 80km nữa mới giảm vận tốc còn bằng 80% so với vận tốc ban đầu thì ô tô đến B chỉ chậm 36 phút so với thời gian dự định. Tính độ dài quãng đường AB ?
Hướng dẫn:
Sau khi đi được 1 giờ, ôtô giảm vận tốc còn 80% vận tốc ban đầu, tức là bằng 4/5 vận tốc ban đầu. Suy ra thời gian đi qua quãng đường sau sẽ bằng \(\dfrac{5}{4}\) so với dự định.
Thực tế xe ô tô đến B chậm hơn dự định 1 giờ nên thời gian dự định đi qua quãng đường sau là 4 giờ, thời gian đi qua thực tế là 5 giờ.
Như vậy ô tô dự định đi cả quãng đường trong 5 giờ.
Nếu sau khi ô tô đi 1 giờ và đi thêm 80km nữa mới giảm tốc độ thì chỉ đến chậm so với dự định 36 phút, nên thời gian ô tô đi 80 km đó nhanh hơn so với khi giảm tốc độ là 24 phút. Do tỉ lệ thời gian cũng là \(\dfrac{4}{5}\) nên thời gian ô tô đi 80 km đó là:
24 x 4 = 96 (phút)
Vận tốc dự định của ô tô là:
80 : 96 x 60 = 50 (km/h)
Độ dài quãng đường AB là:
5 x 50 = 250 (km)
Đáp số: 250 km.
Bài 7: Cho 14 số tự nhiên khác 0 và không có hai số nào bằng nhau. Biết tổng của chúng bằng 106. Tìm số lớn nhất trong các số trên ?
Hướng dẫn:
Tổng 14 số tự nhiên khác 0 đầu tiên là:
1 + 2 + … + 14 = (1 + 14) x 14 : 2 = 105
Do tổng 14 số đã cho là 106 nên 14 số đó phải là: 1; 2; 3; …; 12; 13; và 15
Vậy số lớn nhất trong 14 số là 15.
Đáp số: 15.
Bài 8: Cho hình bình hành ABCD. Gọi P là điểm chính giữa của BC; Q là điểm chính giữa của DC, I là điểm thuộc đoạn DC sao cho DC = 3 x IC. Hai đoạn thẳng PQ và BI cắt nhau tại O. Tính diện tích tam giác APQ khi biết diện tích tam giác OPI bằng 3 \(cm^2\) ?
Hướng dẫn:
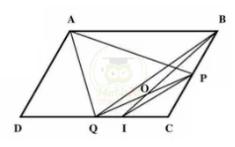
Các em nhìn hình sẽ thấy được rằng để tính được diện tích tam giác APQ thì không thể tính dựa vào công thức vì đề bài không cho chiều cao và cạnh đáy. Vậy bắt buộc chúng ta phải làm theo cách dựa vào diện tích của các hình khác
Theo đề bài:
\(P B=P C;D C=3I C;Q D=\left({\dfrac{3}{2}}\right)I C;Q C=3Q I\)
\({\dfrac{O I}{O B}}={\dfrac{S_{P O I}}{S_{P O B}}}={\dfrac{S_{Q O I}}{S_{Q O B}}}={\dfrac{S_{P O I}+S_{Q O I}}{S_{P O B}+S_{Q O P}}}={\dfrac{S_{I P Q}}{S_{B P Q}}}={\dfrac{\dfrac{1}{3}S_{P Q C}}{S_{P Q C}}}={\dfrac{1}{3}}\)
Do \(S_{O P I}=3cm^{2} \ nên \ S_{P O B}=3\times3=9\left(c m^{2}\right) và \ S_{I P B}=\,S_{O P B}+\,S_{O P I}=12\left(c m^{2}\right)\)
\(S_{I R C}=2S_{I P B}=2\times12=24(c m^{2});\;S_{B C Q}=\left({\dfrac{3}{2}}\right)S_{B I C}=\left({\dfrac{3}{2}}\right)\times24=36\;(c m^{2})\)
\(S_{I B C}=2S_{I P B}=24\,c m^{2} \ và \ S_{A B C D}=4\times S_{B C Q}=4\times36=144\,(c m^{2})\)
\(S_{A P O}=S_{A P C Q}-S_{C P Q}=144\div2-18=54\,c m^{2}\)
Đáp số: 54\(cm^2\)
Bài 9: Một công việc nếu đội thứ nhất làm một mình thì hoàn thành trong 30 giờ, nếu đội thứ hai làm một mình thì hoàn thành trong 12 giờ. Cũng công việc đó khi đội thứ nhất làm trong một thời gian rồi nghỉ và đội thứ hai làm tiếp, thì tổng số thời gian hai đội hoàn thành công việc là 18 giờ. Hỏi khi đó thì đội thứ hai đã làm trong bao nhiêu giờ ?
Hướng dẫn:
Đội thứ nhất làm một mình thì phải mất 30 giờ mới hoàn thành công việc, trong khi nếu để đội 2 làm tiếp phần còn lại thì chỉ mất 18 giờ. Như vậy phần công việc mà đội 2 đã làm nhanh hơn so với đội 1 là 12 giờ.
Để hoàn thành công việc, đội 2 làm nhanh hơn đội 1 là 18 giờ.
Suy ra phần công việc mà đội 2 đã làm chiếm \(\dfrac{12}{18}\) = \(\dfrac{2}{3}\) (lượng công việc)
Vậy đội 2 đã làm xong:
12 x (\(\dfrac{2}{3}\)) = 8 (giờ)
Đáp số: 8 giờ.
Bài 10: Cho một số tự nhiên có 2014 chữ số. Biết rằng với hai chữ số liên tiếp theo thứ tự đã viết thì tạo thành số có hai chữ số chia hết cho 17 hoặc chia hết cho 23. Nếu chữ số cuối cùng của số đó là chữ số 1 thì chữ số đầu tiên là chữ số nào ?
Hướng dẫn:
Các số có hai chữ số chia hết cho 17 là : 17 ; 34 ; 51 ; 68 ; 85.
Các số có hai chữ số chia hết cho 23 là : 23 ; 46 ; 69 ; 92.
Để ý các chữ số cuối cùng của các số trên đôi một khác nhau, do đó nếu biết chữ số cuối cùng thì xác định được duy nhất chữ số đứng trước nó.
Vì chữ số cuối cùng của số cần tìm là 1 nên chữ số trước nó là 5.
Đứng trước chữ số 5 là chữ số 8
Lập luận tương tự ta thấy số số cần tìm có tận cùng …69234692346851.
Như vậy từ 3 chữ số cuối là 851, các chữ số của số cần tìm lặp lại theo chu kỳ 69234.
Vì số cần tìm có 2014 chữ số nên chữ số đầu tiên là 6.
Đáp số: 6.
Bài 1: Chứng minh rằng nếu có n số tự nhiên có tích bằng n và có tổng bằng 2012 thì n chia hết cho 4 ?
Hướng dẫn:
Xét hai trường hợp n chẵn và n lẻ sau đâu:
a) Nếu n là số lẻ thì do tích n số tự nhiên bằng n lẻ nên tất cả n số đều là các số lẻ, và tổng của n số lẻ là một số lẻ nên không thể bằng 2012 (loại trường hợp này)
b) Nếu n là số chẵn thì do tích n số tự nhiên bằng n nên trong n số đã cho có ít nhất 1 số chẵn. Xét hai khả năng sau đây:
+) Nếu trong n số chỉ có đúng một số chẵn, thì (n – 1) số còn lại đều là các số lẻ, khi đó tổng của (n – 1) số lẻ là một số lẻ, kết hợp với số chẵn duy nhất thì tổng của n số đã cho là một số lẻ và không thể bằng 2012 (loại khả năng này).
+) Nếu trong n số có ít nhất 2 số chẵn thì tích cỉa 2 số này chia hết cho 4. Theo giả thiết, tích của n số tự nhiên bằng n nên suy ra chia hết cho 4.
Bài 2: Cho tam giác ABC có diện tích bằng 600 \(cm^2\). Trên cạnh BC lấy các điểm M và N sao cho BM = CN = \(\dfrac{1} {4}\) BC. Trên cạnh AB lấy điểm E, trên cạnh AC lấy điểm F sao cho ACME là hình thang có đáy là AC và ME; ABNF là hình thang có đáy là AB và NF. Kéo dài EM và FN cắt nhau tại K. Tính diện tích hình ABKC ?
Hướng dẫn:
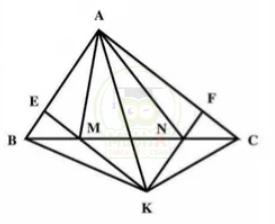
Nối AK. Từ ACME và ABNF là hình thang suy ra ANKB là hình thang và AMKC là hình thang.
Từ các tính chất của hai hình thang này và BN = (\(\dfrac{3}{4}\)) BC; CM = (\(\dfrac{3}{4}\)) CB suy ra:
\(S_{K A B}=S_{NA B}=S_{A B N}\) = \(\dfrac{3}{4}\) \(S_{ABC}=450c m^{2}\)
\(S_{K A C}=S_{MAC}=S_{ACM}\) = \(\dfrac{3}{4}\) \(S_{ACB}=450c m^{2}\)
Vậy \(S_{ABKC}=S_{K A B}+S_{K A C}=900c m^{2}\)
Đáp số: 900\(cm^2\).
Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Chuyên Amsterdam năm học 2014 - 2015.
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS HÀ NỘI AMSTERDAM để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.
Lưu ý: Các em cần Tạo Tài khoản và Đăng Nhập để có thể xem được những nội dung này.