
Để giúp các em học sinh chuẩn bị tốt cho kỳ thi tuyển sinh vào lớp 6 Trường Chuyên Amsterdam, Thầy/cô MATHX biên soạn gửi đến phụ huynh và các em hướng dẫn giải chi tiết các dạng bài trong đề thi lên lớp 6 các năm của trường chuyên Hà Nội Amsterdam. Hy vọng rằng tài liệu giải chi tiết này sẽ là công cụ hữu ích, giúp các em nắm bắt được cấu trúc của đề thi, rèn luyện kỹ năng giải bài một cách tốt linh hoạt và chủ động hơn. Chúc các em học sinh có những kết quả xuất sắc trong kỳ thi sắp tới và đạt được vé vào cổng trường mong muốn.
Phụ huynh và các em học sinh xem thêm danh sách đáp án đề thi vào 6 Amsterdam qua các năm tại đây:
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2005 2006
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2006 2007
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2007 2008
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2008 2009
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2009 2010
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2010 2011
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2011 2012
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2012 2013
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2013 2014
GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2014 2015
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2019 - 2020
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2020 - 2021
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2022 - 2023
GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2023 - 2024
Môn: Toán
Năm học: 2012 - 2013
Bài 1: Tính giá trị của biểu thức: \(A = \dfrac {154 + 919 + 146 + 781}{823-217+ 533-139} ?\)
Hướng dẫn:
Sử dụng phép giao hoán các số hạng để tính nhanh ta có:
\(A={\dfrac{(154+146)+(919+781)}{(823+533)-(217+139)}}={\dfrac{300+1700}{1356-356}}={\dfrac{2000}{1000}}=2\)
Đáp số: 2.
Bài 2: Tìm x biết: \(\left(\dfrac{1}{3\times5}+\dfrac{1}{5\times7}+\dfrac{1}{7\times9}+\cdot\cdot\cdot+\dfrac{1}{19\times21}\right)\times x=\dfrac{9}{7} \ ?\)
Hướng dẫn:
\({\dfrac{1}{3\times5}}+{\dfrac{1}{5\times7}}+{\dfrac{1}{7\times9}}+\ldots+{\dfrac{1}{19\times21}}={\dfrac{1}{2}}\!\left({\dfrac{2}{3\times5}}+{\frac{2}{5\times7}}+{\dfrac{2}{7\times9}}+\ldots+{\dfrac{2}{19\times21}}\right)\)
\(={\dfrac{1}{2}}\left[\left({\dfrac{1}{3}}-{\dfrac{1}{5}}\right)+\left({\dfrac{1}{5}}-{\dfrac{1}{7}}\right)+\left({\dfrac{1}{7}}-{\dfrac{1}{9}}\right)+...+\left({\dfrac{1}{19}}-{\dfrac{1}{21}}\right)\right]={\dfrac{1}{2}}\left({\dfrac{1}{3}}-{\dfrac{1}{21}}\right)={\dfrac{1}{2}}\times{\dfrac{2}{7}}={\dfrac{1}{7}}\)
=> x = 9.
Đáp số: 9.
Bài 3: Mỗi phút một người hít thở 15 lần, mỗi lần hít 0,55 lít không khí, mỗi lít không khí nặng 1,3 g. Hỏi trong 5 ngày người đó hít bao nhiêu gam không khí ?
Hướng dẫn:
1 ngày có 24 giờ.
1 giờ có 60 phút.
5 ngày người đó hít số gam không khí là:
\(5\times24\times60\times15\times0,55\times1,3\ =77220\left(g a m\right)\)
Đáp số: 77220 g.
Bài 4: Tổ I trồng được 15 cây, tổ II trồng được hơn tổ I 4 cây. Tổ III trồng hơn trung bình cộng 3 tổ là 6 cây. Tính số cây tổ III trồng được ?
Hướng dẫn:
Gọi số cây tổ III trồng được là a (cây).
Trung bình cộng số cây 3 tổ trồng được là a - 6 (cây).
Tổng số cây 3 tổ trồng được là:
15 + (15 + 4) + a (cây)
Theo đề ra chúng ta sẽ có tổng số cây 3 tổ = trung bình x 3 nên:
15 + (15 + 4)+ a = 3 x (a - 6)
= 34 + a = 3 x a - 18
= 34 + 18 = 3 x a - a = 2 x a
= a = 52 : 2 = 26 (cây)
Vậy trồng được 26 cây.
Đáp số: 26 cây.
Bài 5: Cho 3 số có tổng 2052. Biết số thứ nhất bằng \(\dfrac{3}{4}\) số thứ hai, số thứ hai bằng \(\dfrac{1}{3}\) số thứ ba. Tìm mỗi số ?
Hướng dẫn:
Gọi số thứ nhất là 3 x a
Số thứ nhất bằng \(\dfrac{3}{4}\) số thứ 2 nên số thứ hai là 4 x a
Số thứ hai bằng \(\dfrac{1}{3}\) số thứ ba nên số thứ ba là 3 x (4 x a) = 12 x a.
Tổng 3 số là:
3 x a + 4 x a + 12 x a = 2052.
=> 19 x a = 2052 = a = 108.
Vậy số thứ nhất, số thứ hai, số thứ ba lần lượt là: 324, 432, 1296.
Đáp số: 324, 432, 1296.
Bài 6: Hai ô tô cùng khởi hành một lúc tại A và B để đi cùng chiều tới địa điểm C. Biết rằng A cách B là 48 km. Sau 3 giờ, ô tô xuất phát từ A đuổi kịp ô tô xuất phát từ B tại điểm C. Biết tỉ số vận tốc của ô tô đi từ A và ô tô đi từ B là \(\dfrac{5}{3}\) . Tính quãng đường BC ?
Hướng dẫn:
Hiệu của hai vận tốc là: 48 : 3 = 16 (km/h)
Hiệu số phần bằng nhau là: 5 - 3 = 2 (phần)
Sau 3 giờ, hiệu quãng đường 2 ô tô đã đi là 48 km nên hiệu vận tốc 2 xe là:
48 : 3 = 16 (km/h)
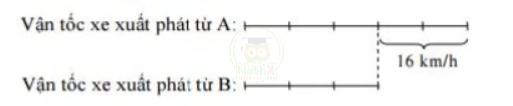
Vận tốc của xe xuất phát từ B là:
\((16:2)\times3=24\) (km/h)
Quãng đường BC là:
3 x 24 = 72 (km)
Đáp số: 72 km.
Bài 7: Tổng 2 bán kính của 2 hình tròn bằng 16 cm. Hình tròn lớn có diện tích gấp 9 lần diện tích hình tròn nhỏ. Tìm chu vi của mỗi đường tròn ?
Hướng dẫn:
Diện tích hình tròn lớn gấp 9 lần diện tích hình tròn nhỏ nên bán kính hình tròn lớn gấp 3 lần bán kính hình tròn nhỏ.
Mặt khác, tổng 2 bán kính là 16 cm suy ra bán kính hình tròn nhỏ là 4 cm, bán kính hình tròn lớn là 12 cm.
Chu vi hình tròn nhỏ là:
4 x 2 x 3,14 = 25,12 (cm)
Chu vi hình tròn lớn là:
12 x 2 x 3,14 = 75,36 (cm)
Đáp số: Chu vi hình tròn nhỏ: 25,12 cm; Chu vi hình tròn lớn: 75,36 cm.
Bài 8: Tuổi bố năm nay gấp 2,2 lần tuổi con. Hai mươi lăm năm về trước tuổi bố gấp 8,2 lần tuổi con. Hỏi khi tuổi bố gấp 3 lần tuổi con thì con bao nhiêu tuổi?
Hướng dẫn:
Hiệu tuổi bố và con không đổi, gọi hiệu đó là a.
Năm nay tuổi bố gấp 2,2 lần tuổi con nên a gấp 1,2 lần tuổi con hiện tại
25 năm trước tuổi bố gấp 8,2 lần tuổi con nên a gấp 7,2 lần tuổi con khi đó.
Khi tuổi bố gấp 3 lần tuổi con thì a gấp 2 lần tuổi con khi đó.
Do 7,2 gấp 6 lần 1,2 nên tuổi con hiện tại gấp 6 lần tuổi con 25 năm trước.
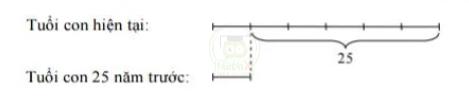
Tuổi con 25 năm trước là
25 : 5 = 5 (tuổi)
Hiệu tuổi bố và con là:
7,2 x 5 = 36 (tuổi)
Khi tuổi bố gắp 3 lẳn tuổi con thì tuổi con là
36 : 2 = 18 (tuổi)
Đáp số: 18 tuổi
Bài 9: Cho dãy số 2, 17, 47, 92, 152, … Tìm số hạng thứ 120 của dãy ?
Hướng dẫn:
Nhận xét quy luật:
Số thứ nhất là: 2
Số hạng thứ 2 là: 17 = 2 + 15 = 2 + 15 x 1
Số hạng thứ 3 là: 47 = 2 + 45 = 2 + 15 x 3 = 2 + 15 x (1 + 2)
Số hạng thứ 4 là: 92 = 2 + 90 = 2 + 15 x 6 = 2 + 15 x (1 + 2 + 3)
Số hạng thứ 5 là: 152 = 2 + 150 = 2 + 15 x 10 = 2+ 15 x (1 + 2 + 3 + 4)
Vậy số hạng thứ 120 là :
2+15 x (1 + 2+ 3 +... + 118 + 119) = 107102
Giải thích cách tính tông:
1 + 2 + 3 +...+ 119 = \({\dfrac{(1+119)\times119}{2}}=7140\)
2 + 15 x 1740 = 2 + 107100 = 107102
Đáp số: 107102.
Bài 10: Sách Khoa học và Lịch sử được xếp vào 5 ngăn: Ngăn một có 23 quyển, ngăn hai có 5 quyển, ngăn ba có 16 quyển, ngăn bốn có 22 quyển, ngăn năm có 14 quyển. Sau khi lấy đi số sách trong một ngăn thì số sách Khoa học trong 4 ngăn còn lại gấp 3 lần số sách Lịch sử. Hỏi 4 ngăn còn lại có bao nhiêu sách mỗi loại?
Hướng dẫn:
Số sách Khoa học trong.4 ngăn còn lại gấp 3 lần số sách Lịch sử nên tổng số sách còn lại chia hết cho 4.
Tổng số sách ban đầu là : 23 + 5 + 16 + 22 + 14 = 80 (quyển)
Do 80 chia hết cho 4 nên số sách trong ngăn lấy đi cũng chia hết cho 4.
Vậy ngăn bị lấy đi có 16 quyền, tông số sách còn lại là:
80 - 16 = 64 (quyển)
Số sách Lịch sử còn lại là:
64 : 4= 16 (quyển)
Số sách Khoa học còn lại là:
64 - 16 = 48 (quyển)
Đáp số: 16 quyển và 48 quyển.
Bài 1: Có 22 ô tô gồm 3 loại: loại 4 bánh chở được 6 tấn, loại 6 bánh chở được 8 tấn, loại 8 bánh chở 8 tấn. Số xe đó có tất cả 126 bánh và có thể chở cùng một lúc được 158 tấn. Hỏi mỗi loại có bao nhiêu xe ?
Hướng dẫn:
Giả sử cả 3 loại xe đều là loại chở được 6 tấn thì:
Số tấn chở được là: 22 x 6 = 132 (tấn)
Số tấn ít hơn thực tế chở được là: 158 - 132 = 26 (tấn)
Số lượng bánh xe là: 22 x 4= 88 (bánh xe)
Số bánh xe ít hơn thực tế là: 126 - 88 = 38 (bánh xe).
Nếu thay mỗi xe 6 tắn bằng xe 8 tấn thì:
Mỗi xe sẽ chở nhiều hơn số tấn là : 8 - 6 = 2 (tấn)
Số xe chở được 8 tấn thay thế xe 6 tấn là: 26 : 2 = 13 (xe)
Tới đây chúng ta đã biết số xe chở được ð tắn có 22 - 13 = 9 (xe) và số xe chở được 8 tấn là 13 (xe) bao gồm xe 6 bánh và xe 8 bánh.
Tổng số bánh xe của xe 6 tắn là: 9 x 4 = 36 (bánh xe)
Tổng số bánh xe của xe 8 tắn là: 126 - 36 = 90 (bánh xe)
Giả sử tất cả các xe chở được 8 tấn đều có 6 bánh thì số bánh xe sẽ là:
13 x 6 = 78 (bánh xe)
Vậy số bánh xe ít hơn so với thực tế là: 90 - 78 = 12 (bánh xe)
Mỗi xe 8 bánh hơn xe 6 bánh số bánh xe là: 8 - 6 = 2 (bánh xe)
Số xe 6 bánh cần thay bằng xe 8 bánh là: 12 : 2 = 6 (xe)
Vậy số xe 6 bánh sẽ là: 13 - 6 = 7 (xe)
Đáp số: 9 xe 4 bánh. 7 xe 6 bánh và 6 xe 8 bánh.
Bài 2: Cho tứ giác ABCD có diện tích là 1216cm². Cho M, N, P trên AB sao cho AM = MN = NP = PB. Cho E, F, G trên D sao cho DE = EF = FG = GC. Tính diện tích tứ giác NPFE ?
Hướng dẫn:
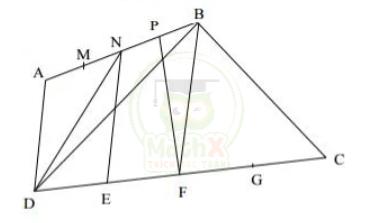
Nối DN, BF.
\(S_{NFB}\) = \(2S_{NFP}\)
\(S_{NFD}\) = \(2S_{NFE}\)
=> \(S_{NBFD} = 2 S_{NPFE}\)
Ta có:
\(S_{ADN} = S_{BDN}\)
\(S_{CBF} = S_{DBF}\)
=> \(S_{ABCD} = 2S_{NBFD}\)
Vậy \(S_{ABCD} = 4S_{NBFE}\) hay \(S_{NPFE} = 1216 : 4 = 304 \ (cm^2)\)
Đáp số: 304 \(cm^2\)
Trên đây MATHX đã hướng dẫn các em chữa đề thi vào lớp 6 môn toán THCS Chuyên Amsterdam năm học 2012 - 2013.
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong ÔN THI THCS HÀ NỘI AMSTERDAM để có thể ôn tập hiệu quả hơn và đạt được kết quả tốt trong kì thi sắp tới.
Lưu ý: Các em cần Tạo Tài khoản và Đăng Nhập để có thể xem được những nội dung này.