HƯỚNG DẪN GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2019 2020 - MATHX

 

Thầy/cô MATHX hướng dẫn các em học sinh giải đề tuyển sinh vào lớp 6 Trường Amsterdam năm học 2019-2020. Các em xem đáp án và lời giải chi tiết để hiểu hơn về cách làm cũng như rút ra kinh nghiệm cho mình nhé. Chúc các em học và ôn tập chuẩn bị thật tốt cho kỳ thi vào 6 của mình.

 

Phụ huynh và các em học sinh nhấn vào link sau để tải đề về làm trước khi xem đáp án

 

 

Quý phụ huynh và các em học sinh xem thêm hướng dẫn giải đề thi vào 6 trường Amsterdam các năm tại đây:

 

 

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2005 2006

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2006 2007

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2007 2008

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2008 2009

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2009 2010

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2010 2011

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2011 2012

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2012 2013

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2013 2014

GIẢI CHI TIẾT ĐỀ THI TUYỂN SINH VÀO LỚP 6 TRƯỜNG CHUYÊN AMSTERDAM 2014 2015

GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2019 - 2020

GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2020 - 2021

GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2022 - 2023

GIẢI CHI TIẾT ĐỀ THI VÀO LỚP 6 THPT CHUYÊN HÀ NỘI AMSTERDAM NĂM HỌC 2023 - 2024

 

 

 

ĐỀ TUYỂN SINH VÀO LỚP 6 TRƯỜNG AMSTERDAM (ĐÁP ÁN + LỜI GIẢI CHI TIẾT)

NĂM HỌC 2019 – 2020

Phần I. Trắc nghiệm

 

Bài 1. Tìm số nhỏ nhất có ba chữ số chia hết cho 5 mà tổng các chữ số bằng 10.

Hướng dẫn

Gọi số cần tìm có dạng \(\overline {abc} \) (a khác 0; a, b, c là chữ số)

Vì \(\overline {abc} \) nhỏ nhất => a = 1. Khi đó số cần tìm có dạng \(\overline {1bc} \) .

Mà tổng các chữ số bằng 10 nên a + b + c = 10 => b + c = 9.

Vì \(\overline {1bc} \) chia hết cho 5 => c = 0 hoặc c = 5.

+ c = 0 => b = 9 => 190.

+ c = 5 => b = 4 => 145.

Vì số cần tìm nhỏ nhất nên số thỏa mãn đề bài là 145.

Đáp số: 145.

 

 

 

Bài 2. Cho phân số \(\dfrac{{14}}{{17}} \)  Hỏi phải thêm vào tử số và mẫu số bao nhiêu đơn vị để được phân số bằng phân số \(\dfrac{{6}}{{7}} \).

Hướng dẫn

Vì cùng thêm một số vào tử số và mẫu số của phân số đã cho nên hiệu giữa mẫu số và tử số không thay đổi.

Hiệu giữa mẫu số và tử số là: 17 – 14 = 3

Ta có sơ đồ:

Tử số mới: |------|------|------|------|------|------|  Hiệu: 3

Mẫu số mới:  |------|------|------|------|------|------|------|

Tử số mới là: 3 : (7 – 6) x 6 = 18

Vậy số cần thêm là: 18 – 14 = 4

Đáp số: 4.

 

 

Bài 3. Cho dãy số: 2; 22; 222; …. Hỏi số thứ 21 của dãy chia 9 dư mấy?

Hướng dẫn

Số thứ 21 của dãy số trên là: 22222…..222 (21 số 2)

Tổng các chữ số của số 22222……222 (21 số 2) là:

2 + 2 + 2 + …. + 2 + 2 = 21 x 2 = 42

Ta có 42 chia 9 dư 6 => 22222……222 (21 số 2) chia 9 dư 6.

Đáp số: 6.

 

 

Bài 4. Hiện nay, tuổi mẹ gấp 4 lần tuổi con. 5 năm nữa, tuổi mẹ gấp 3 lần tuổi con. Tính tuổi con hiện nay.

Hướng dẫn

Hiện nay, tuổi con = \(\dfrac{{1}}{{4}} \) tuổi mẹ => Tuổi con = \(\dfrac{{1}}{{4}} \) hiệu số tuổi của 2 mẹ con.

Sau 5 năm nữa, tuổi con = \(\dfrac{{1}}{{3}} \) tuổi mẹ à Tuổi con = \(\dfrac{{1}}{{2}} \) hiệu số tuổi của 2 mẹ con.

5 năm chiếm: \(\dfrac{1}{2} - \dfrac{1}{3} = \dfrac{1}{6}\) (hiệu số tuổi của 2 mẹ con)

Hiệu số tuổi của 2 mẹ con là: 5 x 6 = 30 (tuổi)

Tuổi con hiện nay là: 30 : (4 – 1) x 1 = 10 (tuổi)

Đáp số: 10 tuổi.

 

 

 

Bài 5. Tính diện tích hình sau đây:

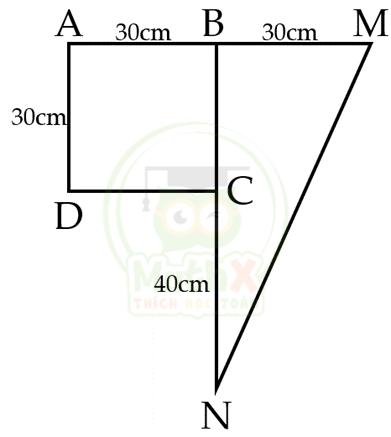
Hướng dẫn

Độ dài đoạn BN là: 30 + 40 = 70 (cm)

Diện tích hình vuông ABCD là: 30 x 30 = 900 (cm2)

Diện tích tam giác BMN là: 30 x 70 : 2 = 1050 (cm2)

Diện tích hình đã cho là: 900 + 1050 = 1950 (cm2)

Đáp số: 1950cm2

 

 

 

Bài 6. Biết diện tích hình tam giác tô đậm là 2cm2. Tính diện tích hình vuông lớn.

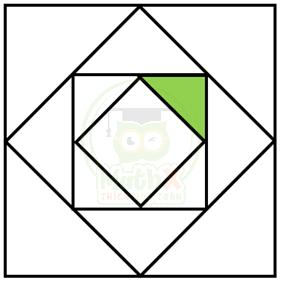
Hướng dẫn

Ta có hình vẽ sau đây:

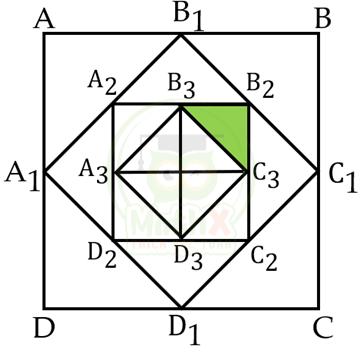
\({S_{{A_2}{B_2}{C_2}{D_2}}} = 2 \times 8 = 16 \) (cm2)

\({S_{{A_1}{B_1}{C_1}{D_1}}} = 2 \times 16 = 32\) (cm2)

\({S_{ABCD}} = 2 \times 32 = 64 \)(cm2)

Đáp số: 64cm2

 

 

 

Bài 7. Biết \(\overline {236b} \) chia hết cho chia hết cho 2; 3; 5. Tính tổng các chữ số a có thể viết được.

Hướng dẫn

\(\overline {236b} \) chia hết cho 2 và 5 à b = 0.

Số đã cho trở thành \(\overline {236b} \) .

Để \(\overline {236b} \) chia hết cho 3 => (a + 2 + 3 + 6 + 0) chia hết cho 3, hay (a + 11) chia hết cho 3 => a = 1; 4; 7

Tổng các chữ số a có thể viết được là: 1 + 4 + 7 = 12.

Đáp số: 12.

 

 

 

Bài 8. Một chiếc ca nô chạy trên khúc sông từ bến A đến bến B. Khi xuôi dòng thì mất 2 giờ. Khi ngược dòng thì mất 4 giờ. Biết rằng, nước chảy với vận tốc 4km/giờ. Hãy tính khoảng cách AB.

Hướng dẫn

Vì vận tốc và thời gian đi hết quãng AB là hai đại lượng tỉ lệ nghịch nên tỉ số giữa vận tốc xuôi dòng và vận tốc ngược dòng là: 4 : 2 = 2

Ta có: Vận tốc xuôi dòng = vận tốc của ca nô + vận tốc dòng nước

Vận tốc ngược dòng = vận tốc của ca nô – vận tốc dòng nước

Suy ra vận tốc xuôi dòng – vận tốc ngược dòng = 2 x vận tốc dòng nước = 2 x 4 = 8 (km/giờ)

Ta có sơ đồ:

Vận tốc ngược dòng:   |-------------|  Hiệu: 8km/giờ

Vận tốc xuôi dòng:  |-------------|-------------|

Vận tốc ngược dòng là: 8 : (2 – 1) x 1 = 8 (km/giờ)

Khoảng cách từ bến A đến bến B là: 8 x 4 = 24 (km)

Đáp số: 24km.

 

 

 

Bài 9. Có 8 hình lập phương nhỏ xếp thành một hình lập phương lớn. Hình lập phương lớn được sơn các mặt màu đỏ. Hỏi mỗi hình lập phương nhỏ được sơn bao nhiêu mặt?

Hướng dẫn

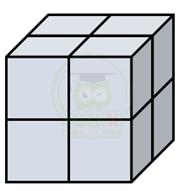
8 hình lập phương nhỏ đều là các hình ở đỉnh à mỗi hình được sơn 3 mặt.

Đáp số: 3 mặt.

 

 

 

Bài 10. Bạn Bình chia 79 viên bi thành 12 nhóm sao cho mỗi nhóm có số bi khác nhau. Hỏi nhóm có số bi nhiều nhất có bao nhiêu viên?

Hướng dẫn

Ta có: 1 + 2 + 3 + 4 + … + 10 + 11 + 12 = 78

=> 79 = 1 + 2 + 3 + 4 + … + 10 + 11 + 13

Vậy nhóm có số bi nhiều nhất là 13 viên.

Đáp số: 13 viên.

 

 

 

Bài 11. Bạn An chạy quanh một sân vận động hình chữ nhật có chiều rộng là 50m; chiều dài là 71,5m và hai nửa hình tròn như hình vẽ. Biết rằng An chạy liên tục từ 7 giờ 30 phút đến 8 giờ với vận tốc trung bình 2,7km/giờ. Hỏi bạn ấy đi được nhiều nhất bao nhiêu vòng trọn vẹn?

Hướng dẫn

Thời gian An chạy là: 8 giờ - 7 giờ 30 phút = 30 phút = 0,5 giờ

Quãng đường mà bạn An chạy là:

0,5 x 2,7 = 1,35 (km)

Đổi: 1,35km = 1350m

Chu vi của sân vận động là: 71.5 x 2 + 50 x 3,14 = 300 (m)

Ta có: 1350 : 300 = 4,5

Vậy An đi được nhiều nhất 4 vòng trọn vẹn.

Đáp số: 4 vòng.

 

 

 

Phần II. Tự luận

 

 

 

Bài 12. Cho hình bình hành ABCD. E là một điểm trên AB. Nối E với C và B với D. Gọi điểm giao nhau giữa EC và BD là F. Diện tích tam giác EFB là 20cm2 và BFC là 50cm2. Tính diện tích hình bình hành ABCD.

Hướng dẫn

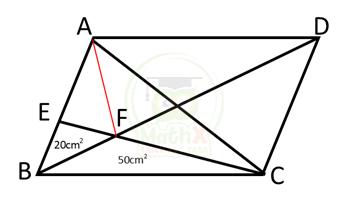
Ta có: S_ABD = S_CBD, đáy BD chung => đường cao hạ từ đỉnh A bằng đường cao hạ từ đỉnh C xuống cạnh BD

S_ABF = S_CBF = 50cm² (vì có chung đáy AF, đường cao hạ từ đỉnh A bằng đường cao hạ từ đỉnh C xuống AF)

S_AEF = S_ABF – S_BEF  = 50 – 20 = 30cm²

=>\(\dfrac{{A{\rm{E}}}}{{BE}} = \dfrac{{{S_{A{\rm{E}}F}}}}{{{S_{BEF}}}} = \dfrac{{30}}{{20}} = \dfrac{3}{2} \)

=> \(\dfrac{{{S_{CAE}}}}{{{S_{CBE}}}} = \dfrac{{A{\rm{E}}}}{{BE}} = \dfrac{3}{2} \Rightarrow {S_{CAE}} = \dfrac{3}{2} \times {S_{CBE}} = \dfrac{3}{2} \times \left( {20 + 50} \right) = 105(c{m^2})\)

\({S_{ABC{\rm{D}}}} = 2 \times {{\rm{S}}_{ABC}} = 2 \times \left( {{S_{CBE}} + {S_{CA{\rm{E}}}}} \right) = 2 \times \left( {70 + 105} \right) = 350\left( {c{m^2}} \right) \)

Đáp số: 350cm2

 

 

 

Bài 13. Giá của 2 quyển sách, 6 quyển vở và 5 cái bút là 154 000 đồng. Giá của 10 quyển sách, 6 quyển vở, 10 cái bút là 374 000 đồng. So sánh giá 1 quyển vở vởi giá 1 quyển sách.

Hướng dẫn

Theo đề bài ta có:

10 quyển sách + 6 quyển vở + 10 cái bút = 374 000 đồng

=> 5 quyển sách + 3 quyển vở + 5 cái bút = 187 000 đồng (1)

Theo bài ra ta lại có:

2 quyển sách + 6 quyển vở + 5 cái bút = 154 000 đồng (2)

Từ (1) và (2) suy ra: 3 quyển sách – 3 quyển vở = 33 000 đồng

=> 1 quyển sách – 1 quyển vở = 11 000 đồng

Vậy giá tiền 1 quyển sách nhiều hơn giá tiền 1 quyển vở là 11 000 đồng.

Đáp số: 11 000 đồng.

 

 

 

Bài 14. Thầy phụ trách chọn các bạn lớp 5A để tham gia các đội, \(\dfrac{1}{3}\) tham gia đội trống, \(\dfrac{1}{3}\) số còn lại tham gia đội kèn, \(\dfrac{1}{3}\) số còn lại sau hai lượt tham gia đội cờ. Số còn lại tham gia đội diễu hành.

a) Sắp xếp các đội thứ tự giảm dần của số học sinh.

b) Giả sử lớp 5A có 54 học sinh. Thầy muốn chọn ra 1 bạn đội cờ, 2 bạn đội kèn và 2 bạn đội trống. Có bao nhiêu cách chọn?

Hướng dẫn

 a) Số học sinh còn lại sau khi tham gia đội trống là:

\(1 - \dfrac{1}{3} = \dfrac{2}{3}\)(số học sinh cả lớp)

Số học sinh tham gia đội kèn là:

\(\dfrac{1}{3} \times \dfrac{2}{3} = \dfrac{2}{9}\) (số học sinh cả lớp)

Số học sinh còn lại sau khi tham gia đội kèn và đội trống là:

\(1 - \dfrac{1}{3} - \dfrac{2}{9} = \dfrac{4}{9}\)(số học sinh cả lớp)

Số học sinh tham gia đội cờ là:

\(\dfrac{1}{3} \times \dfrac{4}{9} = \dfrac{4}{{27}}\)(số học sinh cả lớp)

Số học sinh tham gia đội diễu hành là:

\(1 - \left( {\dfrac{1}{3} + \dfrac{2}{9} + \dfrac{4}{{27}}} \right) = \dfrac{8}{{27}}\)(số học sinh cả lớp)

Vì: \(\dfrac{1}{3} > \dfrac{8}{{27}} > \dfrac{2}{9} > \dfrac{4}{{27}}\)

=> Sắp xếp các đội thứ tự giảm dần của số học sinh là:

Số học sinh tham gia đội trống, số học sinh tham gia diễu hành, số học sinh tham gia đội kèn, số học sinh tham gia đội cờ.

b) Lớp 5A có 54 học sinh

Suy ra: Số học sinh tham gia đội trống là: 18 bạn

Số học sinh tham gia đội kèn là 12 bạn

Số học sinh tham gia đội cờ là 8 bạn

Thầy muốn chọn ra 1 bạn đội cờ, 2 bạn đội kèn và 2 bạn đội trống

=> Có 8 cách chọn ra 1 bạn đội cờ

Có \(\dfrac{{12 \times 11}}{2} = 66 \) cách chọn ra 2 bạn đội kèn

Có \(\dfrac{{18 \times 17}}{2} = 153 \) cách chọn ra 2 bạn đội trống.

Vậy có tất cả số cách chọn thỏa mãn đề bài là:

8 x 66 x 153 = 80784 (cách)

Đáp số:

a) Các đội thứ tự giảm dần của số học sinh là: Số học sinh tham gia đội trống, số học sinh tham gia diễu hành, số học sinh tham gia đội kèn, số học sinh tham gia đội cờ.

b) 80784 cách