
MATHX.VN gửi đến quý phụ huynh và các em học sinh tổng hợp Bộ 5 đề kiểm tra giữa học kì II môn Toán lớp 8 (có đáp án kèm lời giải chi tiết) sách mới. Cách diều - Kết nối tri thức - Chân trời sáng tạo. Học sinh luyện tập lại kiến thức cũng như làm quen với các dạng toán trong đề thi sau khi ôn tập qua đề cương bằng cách trình bày chi tiết lời giải ra vở. Chúc các con ôn tập tốt và đạt kết quả cao trong kì thi sắp tới!
Phụ huynh và các em học sinh xem thêm đề thi giữa kì 2 môn toán lớp 8 năm học 2023 - 2024 tại đây:
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 1
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 2
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 3
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 4
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 5
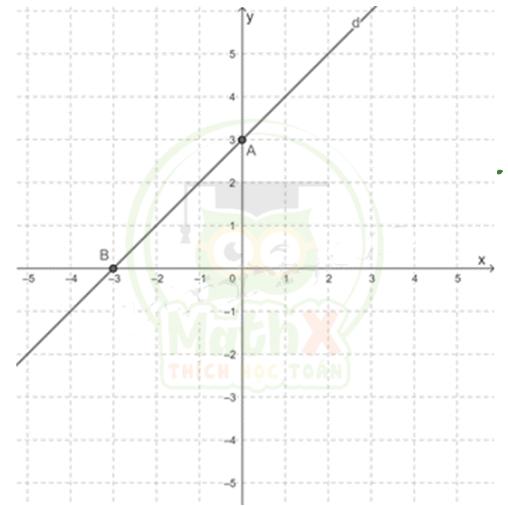
Bài 1. Cho hàm số bậc nhất : y = x + 3 có đồ thị là (d)
a) Vẽ đồ thị (d) của hàm số đã cho.
b) Tìm tọa độ giao điểm của (d) và đường thẳng y = -x + 1.
c) Xác định m để đồ thị hàm số y = (3 - 2m)x + 2 song song với (d).
Lời giải:
a) Cho x = 0 thì y = 0 + 3 = 3. Ta được điểm A(0; 3).
Cho y = 0 thì 0 = x + 3 => x = -3. Ta được điểm B(-3; 0).
Đường thẳng AB chính là đồ thị (d) của hàm số y = x + 3.
b) Phương trình tọa độ giao điểm của (d) và đường thẳng y = -x + 1 là:
x + 3 = -x + 1 ⇔ 2x = -2 ⇔ x = -1.
Với x = -1 => y = -1 + 3 = 2. Ta được điểm C (-1; 2).
Vậy giao điểm của (d) và đường thẳng y = -x + 1 là C (-1; 2).
c) Để hàm số y = (3 - 2m) x + 2 song song với (d) thì 3 – 2m = 1 hay m = 1. Vậy m = 1 thì hàm số y = (3 - 2m) x + 2 song song với (d).
Bài 2. Một cửa hàng bán thanh lò xo màu đen (loại 30kg) như hình vẽ là 40 000 đồng/1 thanh.

a) Viết công thức biểu thị số tiền y (đồng) bỏ ra để mua x (thanh). Hỏi y có phải là hàm số bậc nhất của x hay không?
b) Bạn A đã mua hết số tiền 480 000 đồng. Hỏi bạn A đã mua bao nhiêu thanh?
Lời giải:
a) Số tiền bỏ ra để mua 1 thanh lò xo là 40 000 đồng.
Số tiền bỏ ra để mua x thanh lò xo là: y = 40 000x (đồng)
Vì y có dạng y = ax + b và 40 000 ≠ 0 nên y là hàm số bậc nhất của x.
b) Bạn A mua hết 480 000 đồng nên thay y = 480 000 ta được:
40 000x = 480 000 => x = 12
Vậy bạn A đã mua 12 thanh lò xo.
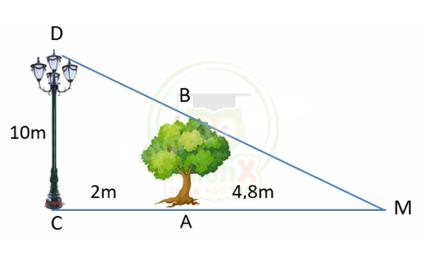
Bài 3. Một cột đèn cao 10m chiếu sáng một cây xanh như hình dưới. Cây cách cột đèn 2m và có bóng trải dài dưới mặt đất là 4,8m. Tìm chiều cao của cây xanh đó (làm tròn đến mét)
Lời giải:
Khoảng cách từ điểm C đến điểm M là: 2 + 4,8 = 6,8 (m).
Vì cột đèn và cái cây đều vuông góc với mặt đất nên ta có AB // CD.
Xét tam giác CMD có AB // CD nên:
\(\dfrac{A B}{A M}\;=\;\dfrac{C D}{C M}\)
\(\dfrac{A B}{4,8}=\dfrac{10}{6,8}\Rightarrow A B=4,8.\dfrac{10}{6,8}=\textstyle\dfrac{120}{17}\approx7\left(m\right)\)
Vậy chiều cao của cây xanh là khoảng 7m.
Bài 4. 1. Tính x trong hình và làm tròn kết quả đến hàng phần mười.

2. Hình thang ABCD (AB // CD) có DC = 2AB. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Chứng minh các tứ giác ABPD, MNPQ là hình bình hành.
b) Tìm điều kiện của hình thang ABCD để MNPQ là hình thoi.
c) Gọi E là giao điểm của BD và AP. Chứng minh ba điểm Q, N, E thẳng hàng.
Lời giải:
1. a)
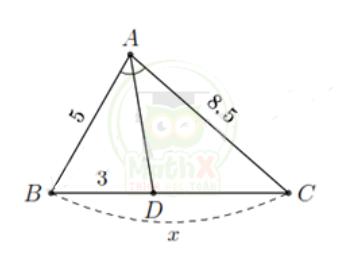
Do AD là đường phân giác trong của góc A nên ta có:
\({\dfrac{D C}{D B}}={\dfrac{A C}{A B}}\Rightarrow D C={\dfrac{A C}{A B}}\cdot D B.\)
Thay số ta có \(D C={\dfrac{8,5}{5}}\cdot3=5,1.\) Khi đó
\(x=D B+D C=3+5,1=8,1.\)
b)
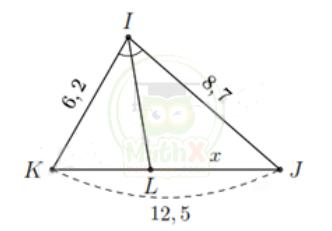
Với KL = 12,5 - x và do IL là đường phân giác trong của góc I nên theo tính chất đường phân giác ta có.
Theo tính chất đường phân giác ta có
\({\dfrac{K L}{L J}}\,=\,{\dfrac{I K}{I J}}\,\Rightarrow\,{\dfrac{12,5-x}{x}}\,=\,{\dfrac{6,2}{8,7}}\,\Leftrightarrow\,x\,=\,{\dfrac{2175}{298}}\,\approx\,7,3.\)
2.
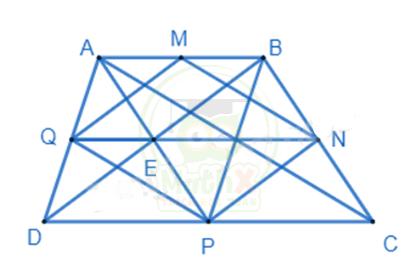
a) Ta có: \(D P=\textstyle{\dfrac{1}{2}}D C=A B;\,A B//C D\Rightarrow A B//D P\) nên ABPD là hình bình hành.
Vẽ AC, ta có MN là đường trung bình
ΔABC => \(M N={\textstyle\dfrac{1}{2}}\,{ A C};M N//AC.\)
Chứng minh tương tự => \(PQ={\textstyle\dfrac{1}{2}}\,{ A C};PQ//AC.\)
=> MN = PQ; PQ // AC nên MNPQ là hình bình hành.
b) Tương tự như đường chéo AC, vẽ BD, ta cũng chứng minh được MQ và NP là đường trung bình của tam giác ABD và BCD nên
\(MQ=NP={\textstyle\dfrac{1}{2}}\,{ BD};MQ//NP//BD.\)
MNPQ là hình thoi khi MN = MQ mà \(M N={\textstyle\dfrac{1}{2}}A C;M Q={\textstyle\dfrac{1}{2}}B D\) (tính chất đường trung bình)
=> AC = BD Khi đó ABCD là hình thang cân.
c) Vì ABPD là hình bình hành nên E là trung điểm của AP.
Xét tam giác ABD có QE là đường trung bình của tam giác ABD nên QE // AB (1)
Xét tam giác DBC có EN là đường trung bình của tam giác DBC nên EN // DC mà DC // AB nên EN // AB (2)
Từ (1) và (2) suy ra từ E kẻ được EQ // AB và EN // AB nên Q, E, N thẳng hàng
Bài 5. Chứng minh rằng nếu a, b, c khác nhau đôi một thì:
\({\dfrac{b-c}{(a-b)(a-c)}}\,+\,{\dfrac{c-a}{(b-c)(b-a)}}\,+\,{\dfrac{a-b}{(c-a)(c-b)}}\,=\,{\dfrac{2}{a-b}}\,+\,{\dfrac{2}{b-c}}\,+\,{\dfrac{2}{c-a}}.\)
Lời giải:
Xét phân thức \({\dfrac{b-c}{(a-b)(a-c)}}={\dfrac{a-c-a+b}{(a-b)(a-c)}}={\dfrac{a-c}{(a-b)(a-c)}}={\dfrac{1}{a-b}}\,-\,{\dfrac{1}{a-c}}.\)
Tương tự ta có: \(\dfrac{c-a}{(b-c)(b-a)}\,=\,\dfrac{1}{b-c}\,-\,\dfrac{1}{b-a}\)
\(\dfrac{a-b}{(c-a)(c-b)}\,\equiv\,\dfrac{1}{c-a}\,-\,\dfrac{1}{c-b}\)
=> \(\dfrac{b-c}{(a-b)(a-c)}\;+\;\dfrac{c-a}{(b-c)(b-a)}\;+\;\dfrac{a-b}{(c-a)(c-b)}\)
= \({\dfrac{1}{a\!-\!b}}\,-\,{\dfrac{1}{a\!-\!c}}\,+\,{\dfrac{1}{b\!-\!c}}\,-\,{\dfrac{1}{b\!-\!a}}\,+\,{\dfrac{1}{c\!-\!a}}\,-\,{\dfrac{1}{c\!-\!b}}\)
= \(\dfrac{1}{a\!-\!b}\,+\,\dfrac{1}{c\!-\!a}\,+\,\dfrac{1}{b\!-\!c}\,+\,\dfrac{1}{a\!-\!b}\,+\,\dfrac{1}{c\!-\!a}\,+\,\dfrac{1}{b\!-\!c}\,\)
= \({\dfrac{2}{a-b}}\,+\,{\dfrac{2}{b-c}}\,+\,{\dfrac{2}{c-a}}\) (đpcm)
Trên đây MATHX đã hướng dẫn các em giải đề thi giữa kì 2 môn toán lớp 8 năm học 2023 - 2024 - đề 3. Ngoài ra các bậc phụ huynh cần cho con em mình học đúng phương pháp và tham khảo các khóa học online tại MATHX.VN để giúp con tự tin chinh phục môn toán nhé.