
MATHX.VN gửi đến quý phụ huynh và các em học sinh tổng hợp Bộ 5 đề kiểm tra giữa học kì II môn Toán lớp 8 (có đáp án kèm lời giải chi tiết) sách mới. Cách diều - Kết nối tri thức - Chân trời sáng tạo. Học sinh luyện tập lại kiến thức cũng như làm quen với các dạng toán trong đề thi sau khi ôn tập qua đề cương bằng cách trình bày chi tiết lời giải ra vở. Chúc các con ôn tập tốt và đạt kết quả cao trong kì thi sắp tới!
Phụ huynh và các em học sinh xem thêm đề thi giữa kì 2 môn toán lớp 8 năm học 2023 - 2024 tại đây:
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 1
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 2
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 3
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 4
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 5
Câu 1: Trong một hộp có 10 tấm thẻ giống nhau được đánh số 11 ; 12 ; … ; 20. Rút ngẫu nhiên một tấm thẻ từ trong hộp. Tính xác suất của các biến cố sau:
a) A: “Rút được tấm thẻ ghi số là số nhỏ hơn 15”.
b) B: “Rút được tấm thẻ ghi số là bội của 3”.
c) C: “Rút được tấm thẻ ghi số nguyên tố”.
Lời giải:
Số kết quả có thể xảy ra khi rút ngẫu nhiên một tấm thẻ từ trong hộp là 10 kết quả.
a) Số kết quả thuận lợi cho biến cố A: “Rút được tấm thẻ ghi số là số nhỏ hơn 15” là 4 kết quả (11; 12; 13; 14)
Xác suất của biến cố A: “Rút được tấm thẻ ghi số là số nhỏ hơn 15” là:
\(P\left(A\right)={\dfrac{4}{10}}\,=\,{\dfrac{2}{5}}.\)
b) Số kết quả thuận lợi cho biến cố B: “Rút được tấm thẻ ghi số là bội của 3” là 3 kết quả (12; 15; 18)
Xác suất của biến cố B: “Rút được tấm thẻ ghi số là bội của 3” là:
\(P\left(B\right)={\dfrac{3}{10}}\)
c) Số kết quả thuận lợi cho biến cố C: “Rút được tấm thẻ ghi số nguyên tố” là 4 kết quả (11; 13; 17; 19)
Xác suất của biến cố C: “Rút được tấm thẻ ghi số nguyên tố” là:
\(P\left(C\right)={\dfrac{4}{10}}\,=\,{\dfrac{2}{5}}.\)
Câu 2: Thống kê số lượt hành khách vận chuyển bằng đường bộ ở Hải Phòng trong các năm 2018; 2019; 2020; 2021; 2022 lần lượt là 55,02; 62,00; 64,20; 57,14; 67,71. (đơn vi : triệu lượt người). (Nguồn : Niên giám thống kê 2023)
a) Lập bảng thống kê số lượt hành khách vận chuyển bằng đường bộ ở Hải Phòng trong các năm theo mẫu sau:

b) Hãy hoàn thiện biểu đồ ở hình bên để nhận được biểu đồ cột biểu diễn các dữ liệu thống kê số lượt hành khách vận chuyển bằng đường bộ ở Hải Phòng trong các năm trên.
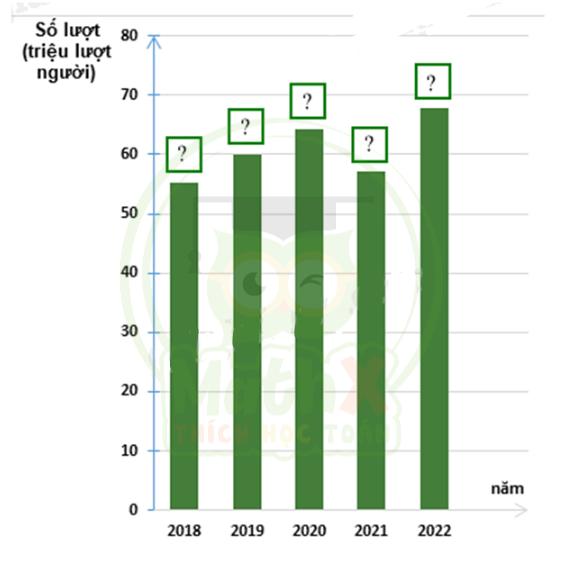
Lời giải:
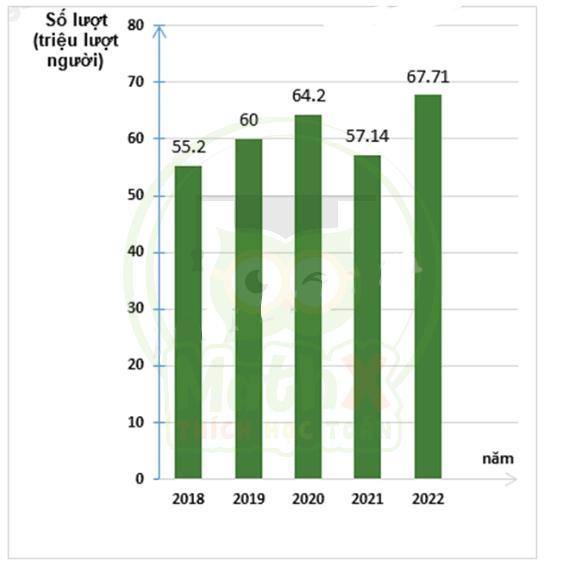
a) Ta có bảng thống kê số lượt hành khách vận chuyển bằng đường bộ ở Hải Phòng trong các năm:
| Năm | 2018 | 2019 | 2020 | 2021 | 2022 |
| Số lượt hành khách (triệu lượt người) | 55,02 | 62,00 | 64,20 | 57,14 | 67,71 |
b) Biểu đồ cột biểu diễn các dữ liệu thống kê số lượt hành khách vận chuyển bằng đường bộ ở Hải Phòng trong các năm trên là:
Câu 3: Bạn An đo được khoảng cách từ vị trí mình đứng (điểm K) đến cây D và cây E ở hai bên hồ nước lần lượt là KD = 18m và KE = 20,25m. Để tính độ dài DE, An xác định điểm A nằm giữa K, D và điểm E nằm giữa K, E sao cho KA = 6,4m, KB = 7,2m và khoảng cách giữa A và B là 32m.
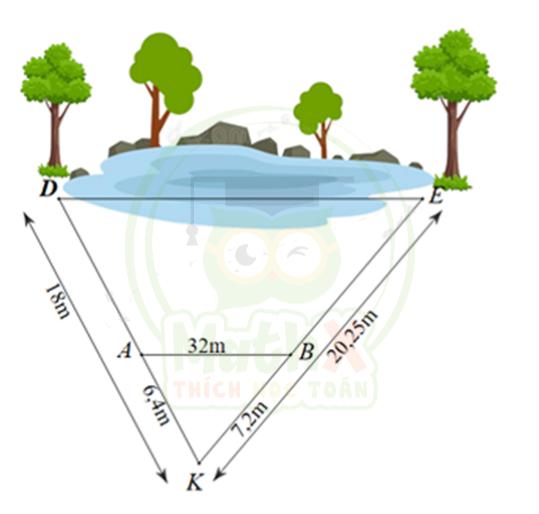
a) Chứng minh \({\dfrac{K B}{K E}}={\dfrac{A K}{A D}}.\)
b) Chứng minh AB // DE
c) Tính khoảng cách giữa D và E.
Lời giải:
a) Ta có:
\({\dfrac{K B}{K E}}\,=\,{\dfrac{7,2}{20,25}}\,=\,{\dfrac{16}{45}}\)
\({\dfrac{A K}{A D}}={\dfrac{6,4}{18}}={\dfrac{16}{45}}\)
=> \({\dfrac{K B}{K E}}={\dfrac{A K}{A D}}.\) (đpcm)
b) Vì \({\dfrac{K B}{K E}}={\dfrac{A K}{A D}}.\) (cmt) nên AB // DE (Định lí Thales đảo trong tam giác)
c) Vì AB // DE nên ta có:
\({\dfrac{A B}{D E}}={\dfrac{A K}{D K}}={\dfrac{16}{45}}\)
\({\dfrac{32}{D E}}={\dfrac{16}{45}}\)
=> \(D E=32:{\dfrac{16}{45}}=90\left(m\right)\)
Vậy khoảng cách giữa D và E là 90m.
Câu 4: Cho tam giác ABC có BC = 20cm. Trên đường cao AH lấy các điểm K, I sao cho AK = KI = IH. Qua I và K kẻ các đường EF và MN song song với BC (E, M ∈ AB, F, N ∈ AC).
a) Tính độ dài các đoạn MN và EF.
b) Tính diện tích tứ giác MNFE biết rằng diện tích tam giác ABC là 300\(cm^2\)
Lời giải:
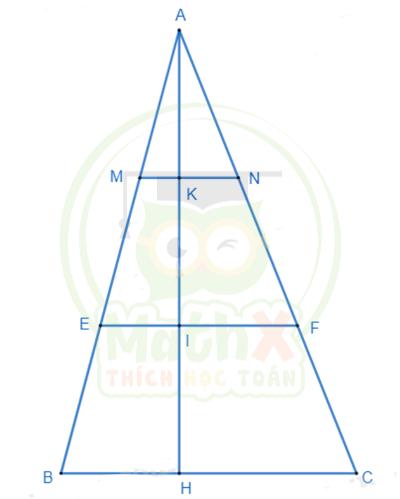
a) Theo bài ra ta có \(A K=K I=I H{\Rightarrow}{\dfrac{A K}{A H}}={\dfrac{1}{3}};{\dfrac{A I}{A H}}={\textstyle\dfrac{2}{3}}.\)
\(\Rightarrow{\dfrac{M K}{B H}}={\dfrac{A K}{A H}}={\dfrac{1}{3}};{\dfrac{E I}{B H}}={\dfrac{A I}{A H}}={\dfrac{2}{3}}\) (1)
Áp dụng hệ quả của định lí Thales vào tam giác ABH có MK // BH và EI // BH
\(\Rightarrow{\dfrac{N K}{C H}}={\dfrac{A K}{A H}}={\dfrac{1}{3}};{\dfrac{F I}{C H}}={\dfrac{A I}{A H}}={\dfrac{2}{3}}\left(2\right)\)
Từ (1) và (2), áp dụng dãy tỉ số bằng nhau ta có:
\({\dfrac{M K}{B H}}={\dfrac{N K}{C H}}={\dfrac{M K+N K}{B H+C H}}={\dfrac{M N}{B C}}={\dfrac{1}{3}}\Rightarrow M N={\dfrac{1}{3}}B C={\dfrac{20}{3}}(c m)\)
\(\dfrac{E I}{B H}\,=\,\dfrac{F I}{C H}\,=\,\dfrac{E I+F I}{B H+C H}\,=\,\dfrac{E F}{B C}\,=\,\dfrac{2}{3}\)
\(\Rightarrow E F=\textstyle{\dfrac{2}{3}}B C=\textstyle{\dfrac{2}{3}}.20=\textstyle{\dfrac{40}{3}}(c m)\)
b) Diện tích tam giác ABC là 300\(cm^2\)
\(\Rightarrow{\dfrac{1}{2}}A H.B C=300\)
\(\textstyle{\dfrac{1}{2}}A H.20=300\)
\(\Rightarrow A H=300:{\dfrac{20}{2}}=30\left(c m\right)\)
Ta có: \(\dfrac{A K}{A H}=\textstyle{\dfrac{1}{3}}\Rightarrow A K=\textstyle{\dfrac{1}{3}}A H=\textstyle{\dfrac{1}{3}}.30=10\left(c m\right)\) => KI = AK = 10cm
Vì MN và EF cùng song song với BC nên MNFE là hình thang. Vì AH ⊥ BC => AH ⊥ MN và AH ⊥ EF
=> KI là đường cao của hình thang MNFE (K ∈ MN; I ∈ EF)
Diện tích hình thang MNFE là:
\(S_{M N F E}={\textstyle\dfrac{1}{2}}(M N+E F)\cdot K I={\textstyle\dfrac{1}{2}}\cdot\left({\textstyle\dfrac{20}{3}}+{\textstyle\dfrac{40}{3}}\right)\cdot10=100\left(c m^{2}\right)\)
Vậy \(S_{MNFE} = 100cm^2\)
Câu 5: Tỉ lệ học sinh nam của lớp 8A là 60%, tổng số bạn lớp 8A là 40. Ngẫu nhiên gặp 1 thành viên nam, xác suất thực nghiệm của biến cố “Gặp một học sinh nam của lớp” là bao nhiêu?
Lời giải:
Số học sinh nam của lớp là: 60% . 40 = 24 (học sinh)
Xác suất thực nghiệm của biến cố “Gặp một học sinh nam của lớp” là:
\(\dfrac{24}{40} = \dfrac{3}{5}\)
Trên đây MATHX đã hướng dẫn các em giải đề thi giữa kì 2 môn toán lớp 8 năm học 2023 - 2024 - đề 1. Ngoài ra các bậc phụ huynh cần cho con em mình học đúng phương pháp và tham khảo các khóa học online tại MATHX.VN để giúp con tự tin chinh phục môn toán nhé.