
Bộ 5 đề kiểm tra giữa kì 2 Toán 9 năm 2023 được MATHX biên soạn nhằm giúp học sinh ôn lại kiến thức và rèn kĩ năng giải bài tập để các em đạt kết quả cao hơn trong kì thi kiểm tra giữa kì 2 sắp tới. Chúc các em học tốt.
Phụ huynh và các em học sinh xem thêm đề thi giữa kì 2 môn toán lớp 9 năm học 2023 - 2024 tại đây:
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 1
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 2
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 3
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 4
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 5
Câu 1: Giải hệ phương trình:
\(\left\{ \begin{array}{} {\dfrac{1}{x+1}}-{\sqrt{y-1}}=-1 \\ {\dfrac{3}{x+1}}+2{\sqrt{y-1}}=7 \\ \end{array} \right.\)
Lời giải:
Điều kiện: \(\left\{ \begin{array}{} x + 1 ≠ 0 \\ y -1 ≥ 0 \\ \end{array} \right.\) <=> \(\left\{ \begin{array}{} x ≠ -1 \\ y ≥ 1 \\ \end{array} \right.\)
Đặt \({\textstyle\dfrac{1}{x+1}}=u\ (u\neq0),\,{\sqrt{y-1}}=v\ \left(v\geq0\right).\)
Khi đó, hệ phương trình trở thành:
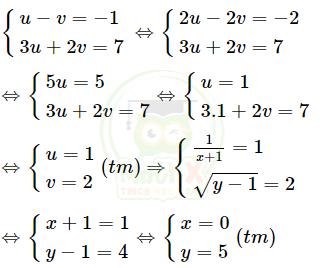
Vậy hệ phương trình có nghiệm duy nhất: (x; y) = (0; 5)
Câu 2: Giải bài toán sau bằng cách lập hệ phương trình:
Một nhóm gồm 15 học sinh nam và nữ, tham gia buổi lao động trồng cây. Cuối buổi lao động, thầy giáo nhận thấy các bạn nam trồng được 30 cây, các bạn nữ trồng được 36 cây. Mỗi bạn nam trồng được số cây như nhau và mỗi bạn nữ trồng được số cây như nhau. Tính số học sinh nam và số học sinh nữ của nhóm, biết rằng mỗi bạn nam trồng được nhiều hơn mỗi bạn nữ 1 cây.
Lời giải:
Gọi số học sinh nam của nhóm là x (học sinh) (x ∈ N*, x < 15)
Số học sinh nữ của nhóm là y (học sinh) (y ∈ N*, y < 15)
Vì nhóm gồm 15 học sinh nên ta có phương trình:
x + y = 15 (1)
Vì mỗi bạn nam trồng được số cây như nhau nên mỗi bạn nam trồng được số cây là: \(\dfrac{30}{x}\) (cây)
Vì mỗi bạn nữ trồng được số cây như nhau nên mỗi bạn nữ trồng được số cây là: \(\dfrac{30}{y}\) (cây)
Vì mỗi bạn nam trồng được nhiều hơn mỗi bạn nữ 1 cây nên ta có phương trình: \(\dfrac{30}{x}\) - \(\dfrac{30}{y}\) = 1 (2)
Từ (1) và (2) ta có hệ phương trình:
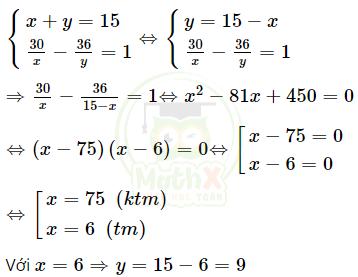
Vậy số học sinh nam của nhóm là 6 học sinh , số học sinh nữ của nhóm là 9 học sinh.
Câu 3: Cho tam giác BC (AB < AC) nhọn nội tiếp đường tròn tâm O Trên cạnh BC lần lượt lấy hai điểm D và E (D nằm giữa B và E) sao cho ∠DAB = ∠EAC. Các tia AD và AE tương ứng cắt đường tròn (O) tại I và J.
a) Chứng minh rằng: Phân giác của góc BAC đi qua điểm chính giữa của cung nhỏ IJ của đường tròn (O)
b) Chứng minh rằng: Tứ giác BCJI là hình thang cân.
c) Kẻ tiếp tuyến xy của đường tròn (O) tại điểm A. Chứng minh rằng: Đường thẳng xy cũng là tiếp tuyến của đường tròn ngoại tiếp tam giác ADE
Lời giải:
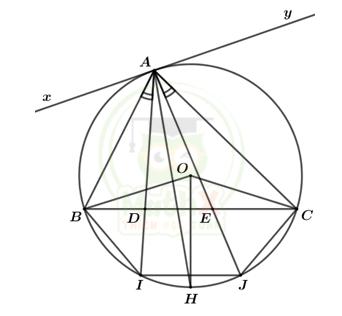
a) Xét đường tròn (O). Giả sử phân giác của góc BAC cắt đường tròn (O) tại H
=> \(\angle B A H=\angle C A H\)
=> \(\angle B A I+\angle I A H=\angle C A J+\angle J A H\)
Mà \(\angle B A I=\angle C A J\) nên \(\angle I A H=\angle J A H.\)
Ta có:
\(\angle I A H={\textstyle{\dfrac{1}{2}}}sđ\,(\angle I A H\) là góc nội tiếp bị chắn bởi cung IH
)
\(\angle J A H={\textstyle{\dfrac{1}{2}}}sđ\,(\angle J A H\) là góc nội tiếp bị chắn bởi cung JH)
Mà \(\angle I A H=\angle J A H.\) (cmt)
⇒ Điểm H nằm chính giữa cung nhỏ IJ
b) Xét đường tròn (O), ta có:
OI = OJ (vì I và J cùng thuộc đường tròn tâm O) (liên hệ giữa cung và dây)
=> OH là đường trung trực của IJ
=> OH ⊥ IJ (1)
Vì AH là phân giác của ∠BAC nên ∠BAH = ∠CAH
\(\angle B A H={\textstyle{\dfrac{1}{2}}}{\mathsf{s đ}} \ (\angle B A H\) là góc nội tiếp bị chắn bởi cung BH)
\(\angle CAH={\textstyle{\dfrac{1}{2}}}{\mathsf{s đ}} \ (\angle C A H\) là góc nội tiếp bị chắn bởi cung CH)
Mà ∠BAH = ∠CAH (cmt)
=> BH = CH (liên hệ giữa cung và dây)
Lại có OB = OC suy ra OH là đường trung trực của BC
=> OH ⊥ BC (2)
Từ (1) và (2) suy ra BC // IJ (quan hệ từ vuông góc đến song song)
⇒ Tứ giác BIJC là hình thang (dấu hiệu nhận biết)
Ta có:
\(\angle IBC={\textstyle{\dfrac{1}{2}}}{\mathsf{s đ}} \) (sđ + sđ)
\(\angle JCB={\textstyle{\dfrac{1}{2}}}{\mathsf{s đ}} \) (sđ + sđ)
Mà, (chứng minh trên)
=> \(\angle I B C=\angle J C B\)
=> BIJC là hình thang cân (dấu hiệu nhận biết)
c) Ta có: \(\angle x A D=\angle x A B+\angle B A D\)
\(\angle A E D=\angle E C A+\angle C A E\ (\angle A E D\) là góc ngoài của ΔAEC)
Xét đường tròn (O) ta có:
(góc tạo bởi tiếp tuyến và dây cung)
(góc nội tiếp bị chắn bởi cung AB)
Hay \(\angle x A B=\angle E C A\ \ \ \ (1)\)
Vì BCJI là hình thang nên BI = CJ (tính chất) (liên hệ giữa cung và dây)
Lại có:
(góc nội tiếp bị chắn bởi cung BI)
(góc nội tiếp bị chắn bởi cung CJ)
Mà (chứng minh trên) suy ra \(\angle B A D=\angle C A E\left(2\right)\)
Cộng (1) với (2) ta có:
\(\angle x A B+\angle B A D=\angle E C A+\angle C A E\)
\(\Rightarrow\angle x A D=\angle A E D\)
=> Đường thẳng xy cũng là tiếp tuyến của đường tròn ngoại tiếp tam giác ADE
Câu 4: Cho a,b,c là các số thực không âm thỏa mãn a + b + c = 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
\(P=a^{2}+b^{2}+c^{2}-3a b.\)
Lời giải:
Vì a,b,c là các số thực không âm thỏa mãn a + b + c = 1 nên 0 ≤ a,b,c ≤ 1
*) Tìm giá trị lớn nhất của biểu thức
\(P=a^{2}+b^{2}+c^{2}-3a b\)
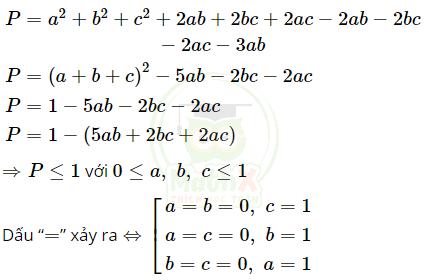
Vậy P đạt giá lớn nhất bằng 1 khi
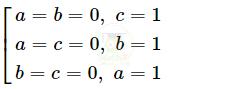
*) Tìm giá trị nhỏ nhất của biểu thức \(P=a^{2}+b^{2}+c^{2}-3a b\)
\(P=a^{2}-2a b+b^{2}+c^{2}-a b\)
\(P=\left(a-b\right)^{2}+c^{2}-a b\)
Áp dụng bất đẳng thức Cô-si cho hai số không âm a và b ta có:
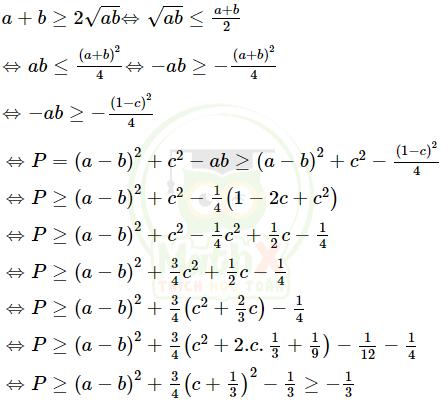
Dấu “=” xảy ra khi và chỉ khi
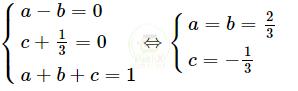
Vậy P đạt giá nhỏ nhất bằng \(-\dfrac{1}{3}\) khi a = b = \(\dfrac{2}{3}\), c = \(-\dfrac{1}{3}\)
Trên đây MATHX đã hướng dẫn các em giải đề thi giữa kì 2 môn toán lớp 9 năm học 2023 - 2024 - đề 3. Ngoài ra các bậc phụ huynh cần cho con em mình học đúng phương pháp và tham khảo các khóa học online tại MATHX.VN để giúp con tự tin chinh phục môn toán nhé.