
Bộ 5 đề kiểm tra giữa kì 2 Toán 9 năm 2023 được MATHX biên soạn nhằm giúp học sinh ôn lại kiến thức và rèn kĩ năng giải bài tập để các em đạt kết quả cao hơn trong kì thi kiểm tra giữa kì 2 sắp tới. Chúc các em học tốt.
Phụ huynh và các em học sinh xem thêm đề thi giữa kì 2 môn toán lớp 9 năm học 2023 - 2024 tại đây:
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 1
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 2
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 3
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 4
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 5
Câu 1: Cho parabol \((P):\,y=-x^{2}\) và đường thẳng \((d):y=2x-3\)
a) Vẽ parabol (P) và đường thẳng (d) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d)
Lời giải:
a) Vẽ Parabol \((P):\,y=-x^{2}\)
Ta có bảng giá trị:
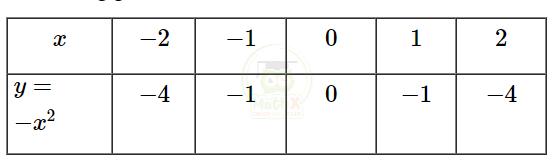
=> \((P):\,y=-x^{2}\) là đường cong Parabol đi qua các điểm có tọa độ \(\left(-2\,;\;-4\right),\left(-1\,;\;-1\right),\left(0\,;\;0\right),\) \(\left(1\,;\ -1\right),\left(2\,;\ -4\right)\)
- Vẽ đường thẳng \((d):y=2x-3\)
Ta có bảng giá trị:
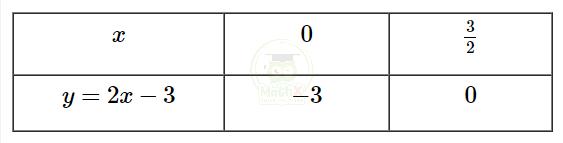
=> \((d):y=2x-3\) là đường thẳng đi qua các điểm có tọa độ \(\left(\operatorname{0}\,\,;\ -3\right),\ \left({\dfrac{3}{2}}\,\,\colon\ 0\right)\)
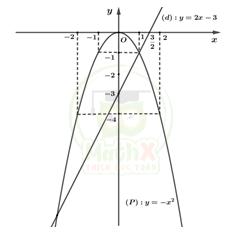
b) Xét phương trình hoành độ giao điểm của (P) và (d) ta có:
\(-x^{2}=2x-3\)
\(\Leftrightarrow x^{2}+2x-3=0\)
\(\Leftrightarrow x^{2}-x+3x-3=0\)
\(\Leftrightarrow\left(x^{2}-x\right)+\left(3x-3\right)=0\)
\(\Leftrightarrow x\left(x-1\right)+3\left(x-1\right)=0\)
\(\Leftrightarrow(x-1)\left(x+3\right)=0\)
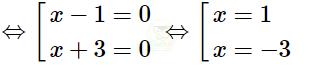
- Với \(x=1{\Rightarrow}y=-1^{2}=-1\)
=> \(A\left(1;\ -1\right)\)
- Với \($x=-3{\Rightarrow}y=-(-3)^{2}=-9\)
=> \(B\left(-3;\ -9\right)\)
Vậy (d) cắt (P) tại hai điểm phân biệt \(A\left(1;\ -1\right)\) và \(B\left(-3;\ -9\right)\)
Câu 2: Giải bài toán bằng cách lập phương trình và hệ phương trình:
Hai tổ sản xuất cùng nhận chung được một đơn hàng, nếu hai tổ cùng làm thì sau 15 ngày sẽ xong. Tuy nhiên, sau khi cùng làm được 6 ngày thì tổ I có việc bận phải chuyển công việc khác, do đổ tổ II làm một mình 24 ngày nữa thì hoàn thành đơn hàng. Hỏi nếu làm một mình thì mỗi tổ làm xong trong bao nhiều ngày?
Lời giải:
Gọi thời gian để tổ I làm một mình hoàn thành xong đơn hàng là x (ngày); (x > 15).
Gọi thời gian để tổ II làm một mình hoàn thành xong đơn hàng là y (ngày); (y > 15).
Trong một ngày, tổ I làm được \(\dfrac{1}{x}\) đơn hàng.
Trong một ngày, tổ II làm được \(\dfrac{1}{y}\) đơn hàng.
Vì hai tổ cùng làm trong 15 ngày thì hoàn thành xong đơn hàng, nên trong một ngày cả hai tổ làm được \(\dfrac{1}{15}\) đơn hàng. Khi đó, ta có phương trình:
\(\dfrac{1}{x}\,+\,\dfrac{1}{y}\,=\,\dfrac{1}{15}\,\,\,\,\,(1)\)
Trong 6 ngày, cả hai tổ làm được \({\dfrac{6}{15}}\,=\,{\dfrac{2}{5}}\) đơn hàng
Trong 24 ngày, tổ II làm được \(\dfrac{24}{y}\) đơn hàng
Vì sau khi cùng làm được 6 ngày thì tổ II làm một mình trong 24 ngày nữa thì hoàn thành xong đơn hàng nên ta có phương trình:
\(\dfrac{2}{5}+\dfrac{24}{y}\,=\,1\quad(2)\)
Từ (1)và (2) ta có hệ phương trình:
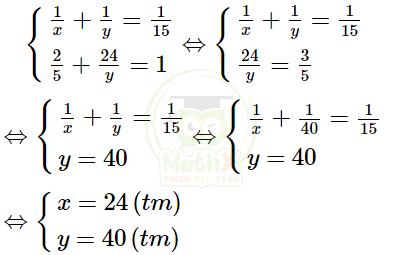
Vậy thời gian để tổ I làm một mình hoàn thành xong đơn hàng là 24 ngày.
Thời gian để tổ II làm một mình hoàn thành xong đơn hàng là 40 ngày.
Câu 3: Cho (O;R), MN là dây không đi qua tâm. C,D là hai điểm bất kì thuộc dây MN (C,D không trùng với M,N). A là điểm chính giữa của cung nhỏ MN. Các đường thẳng AC và AD lần lượt cắt (O) tại điểm thứ hai là E,F
Lời giải:
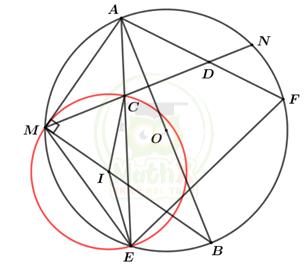
a)
Xét đường tròn (O) có:
(góc có đỉnh nằm bên trong đường tròn)
(góc nội tiếp)
Vì A là điểm chính giữa của cung nhỏ MN nên (liên hệ giữa cung và dây)
\(\Rightarrow\,\angle A C D=\,\angle A F E\) (đpcm)
Theo chứng minh trên, ta có: \(\angle A C D=\angle A F E\)
⇒ Tứ giác CDFE nội tiếp (Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó)
b)
Xét đường tròn (O), ta có:
(góc nội tiếp bị chắn bởi cung AN)
(góc nội tiếp bị chắn bởi cung AM)
Ta lại có: (chứng minh trên) suy ra ∠AMC = ∠AEM
Xét ΔAMC và ΔAEM ta có:
∠A chung
∠AMC = ∠AEM (cmt)
=> ΔAMC = ΔAEM (g.g)
\(\Rightarrow{\dfrac{A M}{A E}}={\dfrac{A C}{A M}}\) (tỷ lệ cặp cạnh tương ứng)
\(\Rightarrow A M^{2}=A E.A C\) (đpcm)
c) Xét đường tròn (O) ta có:
+) \(\angle A M B=90^{0}\) (góc nội tiếp chắn nửa đường tròn)
=> AM ⊥ MB tại M.
+) ∠AMN=∠MEA
(góc nội tiếp bị chắn bởi hai cung bằng nhau và ).
Xét đường tròn ngoại tiếp tam giác MCE ta có:
+) (góc ở tâm)
(góc nội tiếp bị chắn bởi cung MC)
⇒∠MIC = 2∠MEC
+) I là tâm đường tròn ngoại tiếp tam giác MCE
⇒IM = IC = IE (=bán kính)
Vì IM = IC ⇒ ΔMIC cân tại I
⇒∠IMC = ∠ICM (tính chất)
Áp dụng định lý tổng ba góc trong tam giác IMC ta có:
\(\angle I M C+\angle I C M+\angle M T C=180^{0}\)
=> \(2\angle I M C+\angle M I C=180^{0}\) (vì \(\angle I M C=\angle I C M\))
=> \(2\angle I M C+2\angle M E C=180^{0}\) (vì \(\angle M I C=2\angle M E C)\)
=> 2∠IMC + 2∠AMN = \(180^o\) (vì ∠AMN = ∠MEA)
=> ∠IMC + ∠AMN = \(90^o\)
=> ∠AMI = \(90^o\)
⇒AM⊥MI tại M
Mà AM⊥MB tại M (chứng minh trên)
⇒ Ba điểm M,I,B thẳng hàng (đpcm)
Câu 4: Với x,y,z là các số thực dương thỏa mãn đẳng thức \(x y+y z+z x=5.\)
Tìm giá trị nhỏ nhất của biểu thức:
.jpg)
Lời giải:
Vì x,y,z là các số thực dương nên ta có:
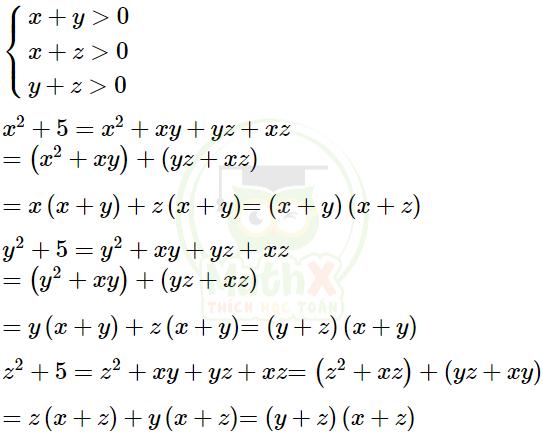
Khi đó, ta có:
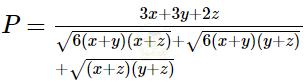
Áp dụng bất đẳng thức Cô-si ta được:
\({\sqrt{6\left(x+y\right)\left(x+z\right)}}={\sqrt{3\left(x+y\right).2\left(x+z\right)}}\)

Dấu “=” xảy ra khi và chỉ khi
Vậy Min = P = \(\dfrac{2}{3}\) <=> \(\left\{ \begin{array}{} x=y=1 \\ z=2 \\ \end{array} \right.\)
Trên đây MATHX đã hướng dẫn các em giải đề thi giữa kì 2 môn toán lớp 9 năm học 2023 - 2024 - đề 4. Ngoài ra các bậc phụ huynh cần cho con em mình học đúng phương pháp và tham khảo các khóa học online tại MATHX.VN để giúp con tự tin chinh phục môn toán nhé.