Trường Toán Online MATHX
MATHX.VN gửi đến quý phụ huynh và các em học sinh tổng hợp Bộ 5 đề kiểm tra giữa học kì II môn Toán lớp 8 (có đáp án kèm lời giải chi tiết) sách mới. Cách diều - Kết nối tri thức - Chân trời sáng tạo. Học sinh luyện tập lại kiến thức cũng như làm quen với các dạng toán trong đề thi sau khi ôn tập qua đề cương bằng cách trình bày chi tiết lời giải ra vở. Chúc các con ôn tập tốt và đạt kết quả cao trong kì thi sắp tới!
Phụ huynh và các em học sinh xem thêm đề thi giữa kì 2 môn toán lớp 8 năm học 2023 - 2024 tại đây:
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 1
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 2
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 3
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 4
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 8 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 5
Câu 6: Cho hình vẽ sau. Biết MN // BC, AM = 2cm, BM = 3cm, AN = 3cm. Độ dài đoạn thẳng NC bằng:
Câu 1: Cho biểu thức \(A=\left({\dfrac{1}{x-2}}-{\dfrac{2x}{4-x^{2}}}+{\dfrac{1}{2+x}}\right)\cdot\left({\dfrac{2}{x}}-1\right)\)
a) Rút gọn A.
b) Tính giá trị của biểu thức A tại x thỏa mãn: \(x^2 + 3x = 0\)
c) Tìm x để A = \(\dfrac{1}{2}\)
d) Tìm x nguyên để A nguyên dương.
Lời giải:
a) ĐKXĐ: \(\left\{\begin{array}{l}{{x-2\neq0}}\\ {{4-x^{2}\neq0}}\\ {{2+x\neq0}}\\ {{x\neq0}}\end{array}\right.\Leftrightarrow\left\{\begin{array}{l}{{x\neq2}}\\ {{x\neq-2}}\\ {{x\neq0}}\end{array}\right.\)
Ta có: \(A=\left({\dfrac{1}{x-2}}-{\dfrac{2x}{4-x^{2}}}+{\dfrac{1}{2+x}}\right)\cdot\left({\dfrac{2}{x}}-1\right)\)
= \(\left({\dfrac{1}{x-2}}\,+\,{\dfrac{2x}{x^{2}-4}}\,+\,{\dfrac{1}{x+2}}\right)\cdot\left({\dfrac{2-x}{x}}\right)\)
\(=\left(\dfrac{x+2}{(x-2)(x+2)}\,+\,\dfrac{2x}{(x-2)(x+2)}\,+\,\dfrac{x-2}{(x-2)(x+2)}\right)\,\cdot\left(\dfrac{2-x}{x}\right)\)
\({}={\dfrac{x+2+2x+x-2}{(x-2)(x+2)}}\cdot{\dfrac{2-x}{x}}\)
\(={\dfrac{4x}{(x-2)(x+2)}}\cdot{\dfrac{2-x}{x}}\)
\(= \dfrac{-4}{x+2}\)
Vậy A = \(= \dfrac{-4}{x+2}\)
b) Ta có: \(x^2 + 3x = 0\)
x (x + 3) = 0
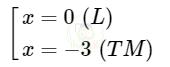
Thay x = -3 vào A, ta được:
\(A={\dfrac{-4}{-3+2}}={\dfrac{-4}{-1}}=4\)
Vậy A = 4 tại x thỏa mãn: \(x^2 + 3x = 0\)
c) Để A = \(\dfrac{1}{2}\) thì \(\dfrac{-4}{x+2}=\dfrac{1}{2}\)
=> -4 . 2 = x + 2
x + 2 = -8
x = -10
Vậy x = -10 thì A = \(\dfrac{1}{2}\)
d) Để A nguyên dương thì \(\dfrac{-4}{x+2}\) nguyên dương => -4 ⋮ (x + 2) và x + 2 < 0 hay (x + 2) ∈ Ước nguyên âm của -4.
Mà Ước âm của -4 là: \(\left\{-1;-2;-4\right\}\)
Ta có bảng giá trị sau:
| x + 2 | -4 | -2 | -1 |
| A = \(\dfrac{-4}{x+2}\) | 1 | 2 | 4 |
| x | -6 (TM) | -4 (TM) | -3 (TM) |
Vậy các giá trị của x để A nguyên dương là: \(x\in\{-6;-4;-3\}.\)
Câu 2: Một tổ sản xuất phải làm 600 sản phẩm trong một thời gian quy định. Do tăng năng suất lao động, mỗi ngày tổ sản xuất đó làm được nhiều hơn kế hoạch 10 sản phẩm. Gọi x (sản phẩm) là số sản phẩm mà tổ sản xuất phải làm trong mỗi ngày theo kế hoạch (x ∈ N∗ ; x < 600).
a) Viết biểu thức biểu thị theo x thời gian tổ sản xuất hoàn thành công việc trước kế hoạch.
b) Giả sử mỗi ngày họ dự định làm 40 sản phẩm. Hãy tính thời gian tổ hoàn thành công việc trước kế hoạch.
Lời giải:
a) Biểu thức biểu thị theo x thời gian tổ sản xuất hoàn thành công việc theo kế hoạch là:
\(\dfrac{600}{x}\) (ngày)
Biểu thức biểu thị theo x thời gian tổ sản xuất hoàn thành công việc thực tế là:
\(\dfrac{600}{x+10}\) (ngày)
Vậy biểu thức biểu thị theo x thời gian tổ sản xuất hoàn thành công việc trước kế hoạch là:
\(\dfrac{600}{x}\) - \(\dfrac{600}{x+10}\) (ngày)
b) Vì mỗi ngày họ dự định làm 40 sản phẩm nên x = 40 (sản phẩm)
Thay x = 40 vào biểu thức biểu thị theo x thời gian tổ hoàn thành công việc trước kế hoạch, ta được:
\(\dfrac{600}{40}-\dfrac{600}{40+10}=15-12=3\) (ngày)
Vậy tổ hoàn thành công việc trước kế hoạch 3 ngày.
Câu 3: Người ta tiến hành đo đạc các yếu tố cần thiết để tính chiều rộng của một khúc sông mà không cần phải sang bờ bên kia sông (hình vẽ bên). Biết BB' -= 20m, BC = 30m và B'C' = 40m. Tính độ rộng x của khúc sông.
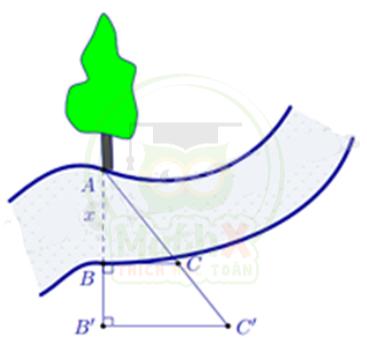
Lời giải:
Ta có: \(\widehat{B}=\widehat{B^{\prime}}=90^{0}\) => BC // B'C'. Áp dụng định lí hai tam giác đồng dạng, ta có ΔABC ~ ΔAB'C'
=> \({\dfrac{A B}{A^{\prime}B^{\prime}}}={\dfrac{B C}{B^{\prime}C^{\prime}}}\)
\({\dfrac{x}{x+20}}={\dfrac{30}{40}}={\dfrac{3}{4}}\)
=> \(4x=3\left(x+20\right)\)
4x = 3x + 60
x = 60 (m)
Vậy độ rộng x của khúc sông là 60m.
Câu 4: Cho ΔABC có AB = 18cm, AC = 24cm, BC = 30cm. Gọi M là trung điểm của BC. Qua M kẻ đường thẳng vuông góc với BC cắt AC, AB lần lượt tại D, E.
a) Chứng minh rằng ΔABC ~ ΔMDC
b) Tính độ dài các cạnh của ΔMDC
c) Tính độ dài BE, EC.
Lời giải:
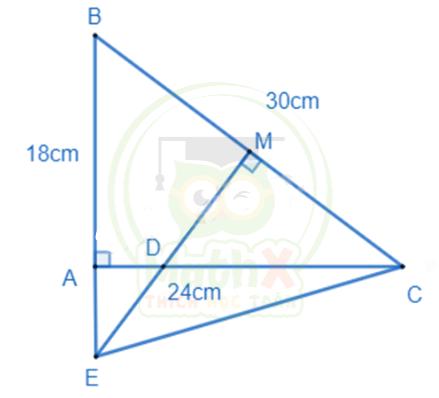
a) Xét ΔABC có: \(A B^{2}+A C^{2}=18^{2}+24^{2}=900=30^{2}=B C^{2}\)
=> ΔABC vuông tại A (định lí Pythago đảo)
Xét ΔABC và ΔMDC ta có:
\(\widehat{A}=\widehat{M}\left(=90^{0}\right)\)
\(\widehat{C}\) chung
=> ΔABC ~ ΔMDC (g.g) (đpcm)
b) Ta có: M là trung điểm của BC nên
\(B M=C M={\textstyle{\dfrac{1}{2}}}B C={\textstyle{\dfrac{1}{2}}}.30=15\left(c m\right)\)
Vì ΔABC ~ ΔMDC nên ta có:
\(\dfrac{A B}{M D}\,=\,\dfrac{B C}{C D}\,=\,\dfrac{A C}{M C}\)
\({\dfrac{18}{M D}}\ ={\dfrac{30}{C D}}\ ={\dfrac{24}{15}}\ ={\dfrac{8}{5}}\)
=> \(M D=18:{\dfrac{\mathrm{8}}{5}}=11,25\)
\(C D=30:{\dfrac{\mathrm{8}}{5}}=18,75\)
c) Xét ΔBME và ΔBAC có:
\(\widehat{M}=\widehat{A}\left(=90^{\circ}\right)\)
\(\widehat{B}\) chung
=> ΔBME ~ ΔBAC (g.g)
=> \({\dfrac{B E}{B C}}={\dfrac{B M}{A B}}\)
\(\dfrac{B E}{30}\,=\,\dfrac{15}{18}\,=\,\dfrac{5}{6}\) => \(B E={\textstyle\dfrac{5}{6}}.30=25\left(c m\right)\)
Xét ΔBME và ΔBAC có:
BM = CM (M là trung điểm của BC)
\(\widehat{B M E}=\widehat{C M E}\left(=90^{0}\right)\)
\(\widehat{ME}\) chung
=> ΔBME = ΔCME (c.g.c)
=> BE = CE = 25cm
Trên đây MATHX đã hướng dẫn các em giải đề thi giữa kì 2 môn toán lớp 8 năm học 2023 - 2024 - đề 2. Ngoài ra các bậc phụ huynh cần cho con em mình học đúng phương pháp và tham khảo các khóa học online tại MATHX.VN để giúp con tự tin chinh phục môn toán nhé.