
Mathx.vn biên soạn gửi tới các em hướng dẫn giải chi tiết đề thi chọn học sinh giỏi lớp 9 môn toán cấp huyện phòng GDĐT huyện Ba Vì năm học 2023 2024. Các em học sinh tải để về làm trước sau đó so sánh kết quả và cách giải chi tiết trong bài viết này. Chúc các em học tập tốt!
Môn thi: Toán - Khối lớp 9
Năm học: 2023 - 2024
Thời gian làm bài: 150 phút
1) Cho \(M=(1-\dfrac{\sqrt{x}}{\sqrt{x}+1}):(\dfrac{\sqrt{x}+4}{\sqrt{x}-3}+\dfrac{\sqrt{x}+3}{4-\sqrt{x}}+\dfrac{\sqrt{x}+3}{x-7\sqrt{x}+12})\) với \(x\ge 0;x\ne 16;x\ne 9\)
a) Rút gọn M
b) Tìm giá trị nhỏ nhất của M
2) Tính giá trị của biểu thức P, biết
\( P=4{{x}^{2023}}+5{{x}^{2024}}+2022\)
với \(x=\sqrt{10-2\sqrt{3}.\sqrt{\sqrt{3}+5+\sqrt{4-2\sqrt{3}}}}-\sqrt{3}\)
Giải
1)
a)
với \(x\ge 0;x\ne 16;x\ne 9\)
\(M=(1-\dfrac{\sqrt{x}}{\sqrt{x}+1}):(\dfrac{\sqrt{x}+4}{\sqrt{x}-3}+\dfrac{\sqrt{x}+3}{4-\sqrt{x}}+\dfrac{\sqrt{x}+3}{x-7\sqrt{x}+12})\)
\(M=\dfrac{1}{\sqrt{x}+1}:\left[ \dfrac{\sqrt{x}+4}{\sqrt{x}-3}-\dfrac{\sqrt{x}+3}{\sqrt{x}-4}+\dfrac{\sqrt{x}+3}{(\sqrt{x}-3)(\sqrt{x}-4)} \right]\)
\(=\dfrac{1}{\sqrt{x}+1}:\left[ \dfrac{(\sqrt{x}+4)(\sqrt{x}-4)-(\sqrt{x}-3)(\sqrt{x}+3)+(\sqrt{x}+3)}{(\sqrt{x}-3)(\sqrt{x}-4)} \right]\)
\(=\dfrac{1}{\sqrt{x}+1}:\dfrac{x-16-(x-9)+\sqrt{x}+3}{(\sqrt{x}-3)(\sqrt{x}-4)} \\ =\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)
b)
\(M=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1}{\sqrt{x}+1}-\dfrac{4}{\sqrt{x}+1}=1-\dfrac{4}{\sqrt{x}+1}\)
Vì \(x\ge 0\Rightarrow \sqrt{x}+1\ge 1\Rightarrow \dfrac{4}{\sqrt{x}+1}\le 4\Rightarrow M\ge -3\)
Dấu ‘‘=” xảy ra khi và chỉ khi x=0
Vậy giá trị nhỏ nhất của M= -3 khi x=0
2)
\(x=\sqrt{10-2\sqrt{3}.\sqrt{\sqrt{3}+5+\sqrt{4-2\sqrt{3}}}}-\sqrt{3}\)
\(=\sqrt{10-2\sqrt{3}.\sqrt{4+2\sqrt{3}}}-\sqrt{3} \\ =\sqrt{10-2\sqrt{3}.(\sqrt{3}+1)}-\sqrt{3} \\ =\sqrt{{{(\sqrt{3}-1)}^{2}}}-\sqrt{3} \\ =-1\)
Với x= -1 giá trị của biểu thức P bằng:
\(P=4.{{(-1)}^{2023}}+5.{{(-1)}^{2024}}+2022=-4+5+2022=2023\)
1) Cho a, b là các số nguyên, chứng minh rằng:
\(Q={{a}^{4}}b-{{a}^{2}}b+a{{b}^{2}}-a{{b}^{4}}\) chia hết cho 6
2) Tìm x, y nguyên thoả mãn:
\({{y}^{2}}=x(x+2)(x+4)(x+6)+15\)
Giải
1)
\(Q={{a}^{4}}b-{{a}^{2}}b+a{{b}^{2}}-a{{b}^{4}}\)
\(\begin{align} & =({{a}^{4}}b-{{a}^{2}}b)-(a{{b}^{4}}-a{{b}^{2}}) \\ & ={{a}^{2}}b({{a}^{2}}-1)-a{{b}^{2}}({{b}^{2}}-1) \\ \end{align} \\ =aba(a-1)(a+1)-abb(b-1)(b+1)\)
Ta có: \(a;(a-1);(a+1)\) là 3 số nguyên liên tiếp.
\(\Rightarrow a(a-1)(a+1) \ \vdots \ 2 \ ; \ a(a-1)(a+1) \ \vdots \ 3\) mà (2,3) =1
\(\Rightarrow a(a-1)(a+1) \ \vdots \ 6\)
Tương tự: \(b(b-1)(b+1) \ \vdots \ 6\Rightarrow Q \ \vdots \ 6\)
2)
\({{y}^{2}}=x(x+2)(x+4)(x+6)+15 =({{x}^{2}}+6x)({{x}^{2}}+6x+8)+15\)
Đặt \({{x}^{2}}+6x+4=t\) khi đó
\({{y}^{2}}=(t-4)(t+4)+15\)
\({{y}^{2}}={{t}^{2}}-1\Leftrightarrow (y-t)(y+t)=-1\)
Ta có bảng sau:
|
y - t |
-1 |
1 |
|
y + t |
1 |
-1 |
|
y |
0 |
0 |
|
t |
1 |
-1 |
+. \({{x}^{2}}+6x+4=1\Leftrightarrow {{(x+3)}^{2}}=6\) không có \(x\in Z\) thoả mãn
+. \({{x}^{2}}+6x+4=-1\)
\(\Leftrightarrow {{x}^{2}}+6x+5=0 \\ \Leftrightarrow (x+1)(x+5)=0 \\\)
\(\Leftrightarrow \left[\begin{array}{c}{{x+1=0}}\\ {{x+5=0}}\end{array}\right. \Leftrightarrow \left[\begin{array}{c}{{x=-1}}\\ {{x=-5}}\end{array}\right.\)
Vậy \((x;y)\in \left\{ (-1;0);(-5;0) \right\}\)
Giải phương trình và bất phương trình sau:
1) \(\dfrac{x+2}{2021}+\dfrac{2x+6}{4040}>\dfrac{x+1}{2022}+\dfrac{2x-1}{4047}\)
2) \(\sqrt{x-3-2\sqrt{x-4}}+\sqrt{x-3+2\sqrt{x-4}}=2\)
Giải
1)
\(\dfrac{x+2}{2021}+\dfrac{2x+6}{4040}>\dfrac{x+1}{2022}+\dfrac{2x-1}{4047}\)
\(\dfrac{x+2}{2021}+1+\dfrac{2x+6}{4040}+1>\dfrac{x+1}{2022}+1+\dfrac{2x-1}{4047}+1\)
\(\begin{align} & \dfrac{x+2023}{2021}+\dfrac{2x+4046}{4040}>\dfrac{x+2023}{2022}+\dfrac{2x+4046}{4047} \\ & \Leftrightarrow (x+2023)(\dfrac{1}{2021}+\dfrac{2}{4040}-\dfrac{1}{2022}-\dfrac{2}{4047})>0 \\ \end{align}\)
Vì
\(\dfrac{1}{2021}+\dfrac{2}{4040}-\dfrac{1}{2022}-\dfrac{2}{4047}>0 \\ \Rightarrow x+2023>0\ \\ \Rightarrow x>-2023\)
Vậy tập nghiệm của bất phương trình là: \(x>-2023\)
2)
ĐK: \(x\ge 4\)
\(\sqrt{x-3-2\sqrt{x-4}}-\sqrt{x-3+2\sqrt{x-4}}=2\)
\(\begin{align} & \sqrt{{{(\sqrt{x-4}-1)}^{2}}}+\sqrt{{{(\sqrt{x-4}+1)}^{2}}}=2 \\ & \Leftrightarrow \left| \sqrt{x-4}-1 \right|+\sqrt{x-4}+1=2 \\ & \Leftrightarrow \left| \sqrt{x-4}-1 \right|=1-\sqrt{x-4}\Leftrightarrow \sqrt{x-4}-1\le 0\Leftrightarrow \sqrt{x-4}\le 1\Leftrightarrow x\le 5 \\ \end{align}\)
Kết hợp điều kiện ta được tập nghiệm của phương trình là: \(4\le x\le 5\)
Bài 4 (6 điểm)
1) Cho tam giác ABC cân tại A, có \( {\widehat{ABC}} = \alpha\) Gọi I là trung điểm của BC. Trên cạnh AB, AC lấy M, N sao cho \( {\widehat{MIN}} = \alpha\) Chứng minh rằng:
a) Tam giác BMI đồng dạng với tam giác CIN. Từ đó suy ra BM.CN không đổi
b) NI là tia phân giác của \( {\widehat{MNC}}\).
2) Cho tam giác ABC vuông tại A, điểm M nằm giữa B và C. Gọi D, E thứ tự là hình chiếu của M trên AC, AB
a) Tìm vị trí của M để DE có độ dài nhỏ nhất.
b) Tam giác ABC có thêm điều kiện gì để với mọi vị trí của M nằm giữa B và C thì các hình chữ nhật ADME có chu vi bằng nhau.
Giải
1)
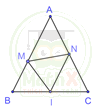
a)
Tam giác BMI có .\( {\widehat{BMI}} + {\widehat{MIB}} = 180^o - \alpha\)
mà \( {\widehat{MIB}} + {\widehat{NIC}} = 180^o - \alpha\)
Suy ra \( {\widehat{BMI}} = {\widehat{NIC}}\)
Xét tam giác BMI và tam giác CIN có
\( {\widehat{BMI}} = {\widehat{NIC}}\) ; \( {\widehat{B}} = {\widehat{C}} \Rightarrow \Delta BMI\backsim \Delta CIN\)
\(\Rightarrow \dfrac{BM}{CI}=\dfrac{BI}{CN}\Rightarrow BM.CN=BI.CI=\dfrac{B{{C}^{2}}}{4}\) không đổi
b)
Xét tam giác MNI và tam giác INC có
\( {\widehat{MIN}} = {\widehat{C}} = \alpha\); mà \(\Delta BMI\backsim \Delta CIN\Rightarrow \dfrac{BI}{CN}=\dfrac{MI}{IN}\Rightarrow \dfrac{CI}{CN}=\dfrac{MI}{IN}\)
\(\Rightarrow \Delta MNI\backsim \Delta INC\)
\( \Rightarrow {\widehat{MNI}} = {\widehat{INC}}\)
=> NI là phân giác của góc \( {\widehat{MNC}}\) .
2)
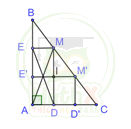
a)
Do D, E là hình chiếu của M trên AC, AB.
Suy ra \( {\widehat{MDA}} = {\widehat{MEA}} = 90^o\) mà \( {\widehat{EAD}} = 90^o\)
Suy ra tứ giác AEMD là hình chữ nhật. Suy ra AM = DE
Suy ra DE nhỏ nhất khi AM nhỏ nhất, khi đó \(AM \bot BC\)
Kết luận: DE có độ dài nhỏ nhất khi AM có độ dài nhỏ nhất tức là \(AM \bot BC\)
b)
Lấy M’ bất kì thuộc BC (M’ ≠ M). Để chu vi hình chữ nhật AEMD bằng chu vi hình chữ nhật AE’M’D’
\(\Leftrightarrow MD+EM=M’D’+E’M’\)
\(\Leftrightarrow MI+ID+EM=M’D’+E’I+IM’\)
mà ID = M’D’; E’I = EM cân \(\Leftrightarrow MI=IM’ \Leftrightarrow \Delta MIM'\)
\(\Leftrightarrow {\widehat{IMM'}} = {\widehat{MM'I}}\) Lại có \({\widehat{IMM'}} = {\widehat{B}}\) ; \({\widehat{MM'I}} = {\widehat{C}}\)
\(\Leftrightarrow {\widehat{B}} ̂= {\widehat{C}} \Leftrightarrow \Delta ABC\) vuông cân tại A
Kết luận: Tam giác ABC cần vuông cân tại A để với mọi vị trí của M nằm giữa B và C thì các hình chữ nhật ADME có chu vi bằng nhau.
Cho các số dương x, y, z thoả mãn: \(x+y+z=3\)
Tìm giá trị nhỏ nhất của biểu thức A, với
\(A=\dfrac{{{(x+1)}^{2}}}{y+z+2}+\dfrac{{{(y+1)}^{2}}}{x+z+2}+\dfrac{{{(z+1)}^{2}}}{x+y+2}\)
Giải:
Đặt \(x+1=a \ ; \ y+1=b \ ; \ z+1=c \Rightarrow a+b+c=6 \ ; \ a,b,c>0\)
\(A=\dfrac{{{a}^{2}}}{b+c}+\dfrac{{{b}^{2}}}{a+c}+\dfrac{{{c}^{2}}}{a+b}\)
Áp dụng bất đẳng thức Cô-si cho hai số dương, ta có:
\(\dfrac{{{a}^{2}}}{b+c}+\dfrac{b+c}{4}\ge 2.\dfrac{a}{2}=a\)
Tương tự:
\(\dfrac{{{b}^{2}}}{a+c}+\dfrac{a+c}{4}\ge 2.\dfrac{b}{2}=b \ ; \ \dfrac{{{c}^{2}}}{a+b}+\dfrac{a+b}{4}\ge 2.\dfrac{c}{2}=c\)
\(\Rightarrow A\ge a+b+c-\dfrac{a+b+c}{2}=\dfrac{a+b+c}{2}=3\)
Dấu ‘‘=” xảy ra khi và chỉ khi
\(\left\{ \begin{align} & 2a=b+c \\ & 2b=a+c \\ & 2c=a+b \\ & a+b+c=6 \\ \end{align} \right.\Leftrightarrow a=b=c=2\)
Vậy giá trị nhỏ nhất của A bằng 3
\(\Leftrightarrow a=b=c=2\)
\(\Leftrightarrow x=y=z=1\)
Trên đây MATHX đã hướng dẫn các em chữa đề thi chọn học sinh giỏi lớp 9 môn toán cấp huyện phòng GDĐT huyện Ba Vì năm học 2023 2024.
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong TÀI LIỆU TOÁN LỚP 9 để có thể tích lũy thêm nhiều kiến thức và ôn tập hiệu quả hơn.
Phụ huynh và các em học có thể tham khảo một số đề thi học sinh giỏi toán lớp 9 khác tại đây:
Đề thi học sinh giỏi THCS tỉnh Quảng Ninh năm 2023
Đề thi học sinh giỏi lớp 9 cấp thành phố Hồ Chí Minh năm học 2022-2023
Đề thi chọn học sinh giỏi lớp 9 THCS tỉnh Tuyên Quang năm học 2022-2023
Đề thi chọn học sinh giỏi cấp tỉnh THCS tỉnh Hưng Yên năm học 2022-2023
Đề thi chọn học sinh giỏi lớp 9 cấp tỉnh Gia Lai năm học 2022-2023
Đề thi chọn học sinh giỏi lớp 9 THCS tỉnh Ninh Bình
HỆ THỐNG CHƯƠNG TRÌNH HỌC CỦA MATHX