ĐỀ KHẢO SÁT CHẤT LƯỢNG ĐẦU NĂM TRƯỜNG THCS XUÂN ĐỈNH - HÀ NỘI NĂM 2025 - 2026

MATHX gửi quý phụ huynh và các em học sinh đề khảo sát chất lượng đầu năm trường THCS Xuân Đỉnh - Hà Nội năm 2025 - 2026

ĐÁP ÁN THAM KHẢO CÂU V

Câu V: Cho tam giác ABC đều cạnh 8 cm. Người ta dựng một hình chữ nhật MNPQ có cạnh MN nằm trên cạnh BC, hai đỉnh P, Q theo thứ tự nằm trên cạnh AC và AB. Tính BM sao cho hình chữ nhật MNPQ có diện tích lớn nhất.

Hướng dẫn

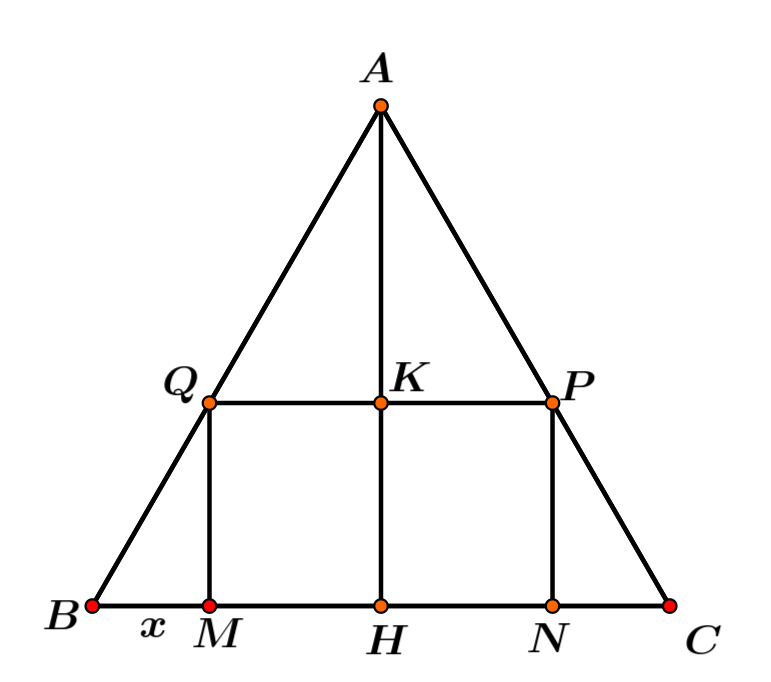
Gọi AH là đường cao của tam giác ABC đều có cạnh là \(8 \, \text{cm}\).

Khi đó \( AH = \dfrac{8\sqrt{3}}{2} = 4\sqrt{3} \, (\text{cm}) \)

Ta chứng minh được \( \triangle BQM \sim \triangle BAH \, (g.g) \) suy ra \( \dfrac{BM}{BH} = \dfrac{QM}{AH} \)

Mà \( BH = \dfrac{BC}{2} = 4 \, (\text{cm}) \) (đường cao vừa là đường trung tuyến trong tam giác đều ABC)

Do đó \( QM = \dfrac{BM \cdot AH}{BH} = \dfrac{x \cdot 4\sqrt{3}}{4} = x\sqrt{3} \, (\text{cm}) \)

Mặt khác \( MN = 8 - 2x \, (\text{cm}) \)

Diện tích hình chữ nhật là:

\( x\sqrt{3}(8 - 2x) = -2\sqrt{3}x^2 + 8\sqrt{3}x \)

\( = -2\sqrt{3}(x^2 - 4x + 4) + 8\sqrt{3} \)

\( = -2\sqrt{3}(x - 2)^2 + 8\sqrt{3} \)

\( \le 8\sqrt{3} \)

Dấu “=” xảy ra khi \( x = 2 \).

Vậy diện tích hình chữ nhật MNPQ lớn nhất bằng \( 8\sqrt{3} \, \text{cm}^2 \) khi \( BM = 2 \, \text{cm} \).