MỘT SỐ CÂU HỎI HÌNH HỌC TRONG ĐỀ THI GIỮA KÌ I LỚP 8 CỦA CÁC TRƯỜNG (BỘ SÁCH: KẾT NỐI TRI THỨC VỚI CUỘC SỐNG)

MATHX gửi quý phụ huynh và các em học sinh một số câu hỏI hình học trong đề thi giữa kì I lớp 8 của các trường (bộ sách kết nối tri thức với cuộc sống) kèm đáp án chi tiết.

Câu 1 (Trường THCS Lý Tự Trọng – Phú Yên)

Cho tứ giác \(ABCD\) có \(AB = BC\). \(AC\) là tia phân giác của góc \(\widehat{A}\). Chứng minh rằng tứ giác \(ABCD\) là hình thang.

Hướng dẫn:

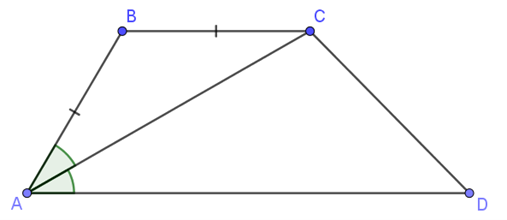
Xét tam giác \(\triangle ABC\) có \(BA = BC\) \(\Rightarrow\) \(\triangle ABC\) cân tại \(B\) (định nghĩa)

\(\Rightarrow \widehat{ABC} = \widehat{BCA}\) (tính chất tam giác cân)

Mà \(\widehat{DAC} = \widehat{BAC}\) (do \(AC\) là phân giác của \(\widehat{BAD}\)).

\(\Rightarrow \widehat{BCA} = \widehat{DAC} \;(=\widehat{BAC})\) mà \(\widehat{BCA}\) và \(\widehat{DAC}\) ở vị trí so le trong

\(\Rightarrow BC \parallel AD\) \(\Rightarrow ABCD\) là hình thang (định nghĩa)

---

Câu 2 (Trường THCS Nguyễn Bỉnh Khiêm – Quảng Nam)

Cho hình bình hành ABCD. Biết \( \widehat{BAD} = 120^{\circ} \).

a. Tính số đo các góc còn lại của hình bình hành.

b. Gọi O là trung điểm của BD. Chứng minh rằng A, O, C thẳng hàng.

Hướng dẫn:

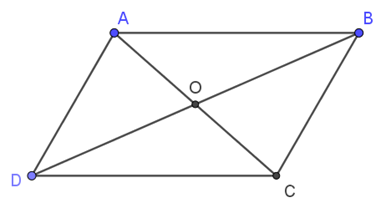
a) Có ABCD là hình bình hành (gt)

⇒ \( \widehat{BAD} = \widehat{DCB}; \ \widehat{ADC} = \widehat{ABC}; \ \widehat{DAB} + \widehat{ADC} = 180^{\circ} \)

Có \( \widehat{DCB} = \widehat{BAD} = 120^{\circ} \);

Có \( \widehat{ADC} = 180^{\circ} - \widehat{BAD} = 180^{\circ} - 120^{\circ} = 60^{\circ} \)

Có \( \widehat{ABC} = \widehat{ADB} = 60^{\circ} \)

b) Có ABCD là hình bình hành;

⇒ BD và AC cắt nhau tại trung điểm của mỗi đường.

Mà O là trung điểm của BD ⇒ O cũng là trung điểm của AC.

⇒ A, O, C thẳng hàng.

---

Câu 3 (Trường THCS Đường Hoa – Quảng Ninh)

Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D, E sao cho \( AD = AE \).

a) Chứng minh rằng BDEC là hình thang cân.

b) Tính các góc của hình thang cân đó biết rằng \( \widehat{A} = 50^{\circ} \).

Hướng dẫn:

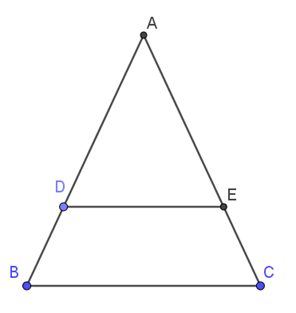
a) Xét tam giác \( \triangle ADE \) có \( AD = AE \) (gt) ⇒ \( \triangle ADE \) cân tại A (định nghĩa)

⇒ \( \widehat{ADE} = \widehat{AED} \) (tính chất tam giác cân)

Có \( \widehat{ADE} + \widehat{AED} + \widehat{A} = 180^{\circ} \Rightarrow 2\widehat{ADE} + \widehat{A} = 180^{\circ} \Rightarrow \widehat{ADE} = \dfrac{180^{\circ} - \widehat{A}}{2} \)

Xét tam giác \( \triangle ABC \) có \( AB = AC \) (gt) ⇒ \( \triangle ABC \) cân tại A (định nghĩa)

⇒ \( \widehat{B} = \widehat{C} \) (tính chất tam giác cân)

Có \( \widehat{B} + \widehat{C} + \widehat{A} = 180^{\circ} \Rightarrow 2\widehat{B} + \widehat{A} = 180^{\circ} \Rightarrow \widehat{B} = \dfrac{180^{\circ} - \widehat{A}}{2} \) mà \( \widehat{ADE} = \dfrac{180^{\circ} - \widehat{A}}{2} \)

⇒ \( \widehat{B} = \widehat{ADE} \) mà \( \widehat{B} \) và \( \widehat{ADE} \) ở vị trí đồng vị ⇒ \( BC // DE \Rightarrow BDEC \) là hình thang

Lại có \( \widehat{B} = \widehat{C} \Rightarrow BDEC \) là hình thang cân

b) Có \( \widehat{B} = \dfrac{180^{\circ} - \widehat{A}}{2} = \dfrac{180^{\circ} - 50^{\circ}}{2} = 65^{\circ} \Rightarrow \widehat{C} = 65^{\circ} \)

Có \( \widehat{BDE} + \widehat{B} = 180^{\circ} \Rightarrow \widehat{BDE} = 180^{\circ} - 65^{\circ} = 115^{\circ} \)

Có BDEC là hình thang cân  \(\Rightarrow \widehat{DEC} = \widehat{BDE} = 115^{\circ} \)

---

Câu 4 (Trường THCS Trần Quang Khải – Khánh Hòa)

Cho tam giác ABC cân tại A. I là trung điểm của AC. Lấy điểm D sao cho I là trung điểm của BD.

a) Chứng minh tứ giác ADCB là hình bình hành.
b) Đường thẳng đi qua điểm D và song song với AC cắt BC tại điểm E. Chứng minh \( AE = BD \).

Hướng dẫn:

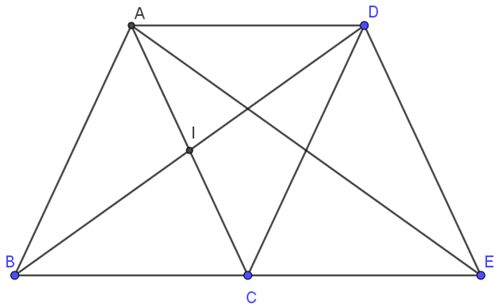
a) Xét tứ giác ADCB có \( BI = ID = \dfrac{1}{2} BD; AI = IC = \dfrac{1}{2} AC \) (gt)

⇒ ADCB là hình bình hành (dấu hiệu nhận biết)

b) Có ADCB là hình bình hành ⇒ \( AD // BC \)

Xét tứ giác ADEC có \( AD // CE; AC // DE \) (gt)

⇒ ADEC là hình bình hành (dấu hiệu nhận biết)

⇒ \( DE // AC \) mà \(\widehat{ BCA }\) và \( \widehat{BED }\) ở vị trí đồng vị

⇒ \( \widehat{BCA} = \widehat{BED} \) lại có \( \widehat{ABC} = \widehat{BCA} \) (do \( \triangle ABC\) cân tại A)

⇒ \( \widehat{ABC} = \widehat{BED} \) ( = \( \widehat{BCA} \))

Xét tứ giác ADEB có \( AD // BE \) ⇒ ADEB là hình thang

Lại có \( \widehat{ABE} = \widehat{BED} \) ⇒ ADEB là hình thang cân ⇒ \( AE = BD \)

---

Câu 5 (Trường THCS Võ Hoành Trang – Hồ Chí Minh)

Cho tam giác \( ABC \) nhọn (\( AB < AC \)). D là trung điểm của \( AB \). Trên tia đối của tia \( DC \) lấy điểm F sao cho \( DF = DC \).

a) Chứng minh tứ giác \( AFBC \) là hình bình hành.

b) Gọi E là trung điểm của \( AC \). Kẻ đường thẳng qua E vuông góc với tia phân giác của góc \( \widehat{ABC}\) tại I và cắt đường thẳng AB, BC lần lượt tại G, H. Chứng minh \( AG = CH \).

Hướng dẫn:

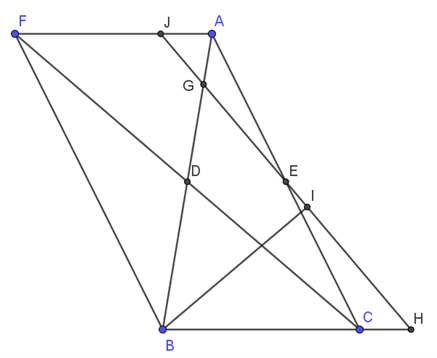
a) Xét tứ giác \( AFBC \) có \( AD = DB = \dfrac{1}{2}AB; CD = FD = \dfrac{1}{2}CF \) (gt).

⇒ \( ABFC \) là hình bình hành (dấu hiệu nhận biết).

⇒ \( AF \parallel BC \).

b) Gọi J là giao của \( GH \) và \( AF \).

Xét \( \triangle AJE \) và \( \triangle CHE \) có:

\( AE = EC \) (gt)

\( \widehat{JEA} = \widehat{HEC} \) (hai góc đối đỉnh)

\( \widehat{JAE} = \widehat{HCE} \) (do \( AF \parallel CH \))

⇒ \( \triangle AJE = \triangle CHE \) (g.c.g)

⇒ \( AJ = CH \) (hai cạnh tương ứng).

Xét \( \triangle BGH \) có \( BI \) là đường cao, \( BI \) là đường phân giác của \( \triangle BGH \).

⇒ \( \triangle BGH \) cân tại B (dấu hiệu nhận biết).

⇒ \( \widehat{H} = \widehat{BGH}\) mà \( \widehat{H} = \widehat{AJG}\) (do \( AJ \parallel CH \) ), \( \widehat{JGA} = \widehat{BGH}\) (hai góc đối đỉnh)

⇒\( \widehat{JGA} = \widehat{GJA}\) \( \Rightarrow \triangle JAG \) cân tại A.

⇒ \( AJ = AG \) mà \( AJ = CH \) ⇒ \( AG = CH \).

---

Câu 6 (Trường THCS Lê Quý Đôn – Thái Bình)

Cho hình bình hành \( ABCD \). Trên cạnh \( AB \) lấy điểm M, trên cạnh \( DC \) lấy điểm N sao cho \( AM = CN \).

a) Chứng minh \( AN \parallel CM \).

b) Gọi O là giao điểm của \( AC \) và \( BD \). Chứng minh O là trung điểm của \( MN \).

Hướng dẫn:

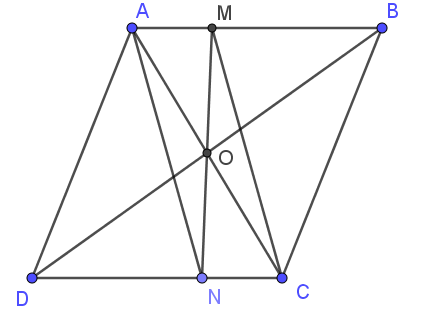
a) Có \( ABCD \) là hình bình hành ⇒ \( AB \parallel CD \).

Xét tứ giác \( AMCN \) có \( AM \parallel CN \); \( AM = CN \) (gt).

⇒ \( AMCN \) là hình bình hành (dấu hiệu nhận biết).

⇒ \( AN \parallel CM \) (tính chất hình bình hành).

b) Có \( ABCD \) là hình bình hành.

⇒ O là trung điểm của \( AC \) và \( BD \).

Do \( AMCN \) là hình bình hành.

⇒ Hai đường chéo \( AC \) và \( MN \) cắt nhau tại trung điểm của mỗi đoạn.

Mà O là trung điểm của \( AC \).

⇒ O cũng là trung điểm của \( MN \).

---

Câu 7 (Trường THCS Vạn Xuân – Hà Nội)

Cho hình thoi \( ABCD \) có \( \widehat{A} = 60^\circ \). Kẻ \( BH \) vuông góc với \( AD \), trên tia đối của tia \( HB \) lấy điểm E sao cho \( HE = BH \).

a) Chứng minh rằng \( ABDE \) là hình thoi.

b) Ba điểm E, D, C thẳng hàng.

c) \( EB = AC \).

Hướng dẫn:

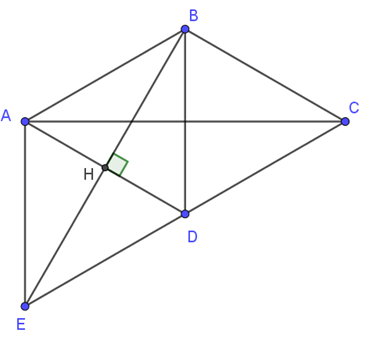
a) Xét \( \triangle ABD \) có \( AB = AD \) (do \( ABCD \) là hình thoi).

⇒ \( \triangle ABD \) cân tại A mà \( \widehat{BAD} = 60^\circ \) ⇒ \( \triangle ABD \) đều ⇒ \( \widehat{ABD} = 60^\circ \).

Mà \( BH \perp AD \) ⇒ \( AH = HD = \dfrac{1}{2}AD \) (tính chất tam giác đều).

Xét tứ giác \( ABDE \) có: \( AH = HD = \dfrac{1}{2}AD; \quad BH = HE = \dfrac{1}{2}BE \).

⇒ \( ABDE \) là hình bình hành (dấu hiệu nhận biết).

Mà \( AD \perp BE \) ⇒ \( ABDE \) là hình thoi.

b) Có \( ABDE \) là hình thoi ⇒ \( \widehat{AED} = \widehat{ABD} = 60^\circ; \widehat{BAE} = \widehat{BDE} \).

Lại có \( \widehat{BDC} + \widehat{AED} + \widehat{BAE} + \widehat{BAD} = 360^\circ \) ⇒ \( \widehat{BDE} = 120^\circ \).

Vì \( AB \parallel CD \) ⇒ \( \widehat{ABD} = \widehat{BDC} \) (hai góc so le trong bằng nhau).

⇒ \( \widehat{BDC} = 60^\circ \).

Có \( \widehat{EDB} + \widehat{BDC} = 120^\circ + 60^\circ = 180^\circ \).

⇒ E, D, C thẳng hàng.

c) Có \( \widehat{BCD} = \widehat{BAD} = 60^\circ \) (do \( ABCD \) là hình thoi).

Mà \( \widehat{AED} = 60^\circ \) ⇒ \( \widehat{AED} = \widehat{BCD} \).

Xét tứ giác \( ABCE \) có \( AB \parallel CE \).

⇒ \( ABCE \) là hình thang mà \( \widehat{AEC} = \widehat{BCE} \).

⇒ \( ABCE \) là hình thang cân.

⇒ \( BE = AC \) (tính chất hình thang cân).

---

Câu 8 (Trường THCS Tân Bình – Hải Dương)

Cho tam giác \( ABC \) vuông tại \( A \) (\( AB > AC \)), trung tuyến \( AM \). Kẻ \( MD \perp AB \) tại \( D \), \( ME \perp AC \) tại \( E \).

a) Chứng minh tứ giác \( ADME \) là hình chữ nhật.

b) Gọi \( O \) là trung điểm của \( ME \). Chứng minh \( DM = EC \) và ba điểm \( D, O, C \) thẳng hàng.

c) Tam giác \( ABC \) cần thêm điều kiện gì để tứ giác \( ADME \) là hình vuông.

Hướng dẫn:

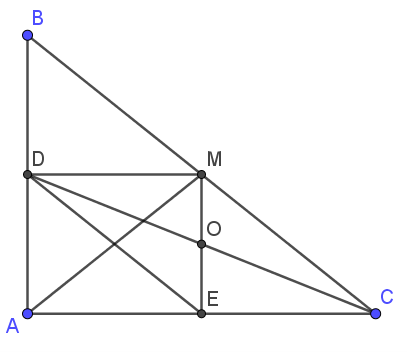
a) Có \( MD \perp AB \); \( ME \perp AC \) ⟹ \( \widehat{MDA} = \widehat{MEA} = 90^\circ \)

Xét tứ giác \( ADME \) có: \( \widehat{MDA} = \widehat{MEA} = \widehat{DAE} = 90^\circ \)
⟹ \( ADME \) là hình chữ nhật (Dấu hiệu nhận biết)

b) Xét \( \triangle ABC \) có \( \widehat{BAC} = 90^\circ \); \( AM \) là trung tuyến của \( \triangle ABC \)
⟹ \( AM = MC = BM = \dfrac{1}{2}BC \)

⟹ \( \triangle AMC \) cân tại \( M \) (Dấu hiệu nhận biết)

Mà \( ME \perp AC \) (gt) ⟹ \( AE =EC= \dfrac{1}{2}EC \)

Mà \( DM = EC \) (Do \( ADME \) là hình chữ nhật)
⟹ \( DM = EC (= AE) \)

Xét tứ giác \( DMCE \) có \( DM \parallel EC \); \( DM = EC \)
⟹ \( DMCE \) là hình bình hành.

Do \( CD \) và \( ME \) cắt nhau tại trung điểm của mỗi đường
Mà \( O \) là trung điểm \( ME \)  ⟹ \( O \) cũng là trung điểm \( CD \) ⟹ \(C, O,D \) thẳng hàng

c) Giả sử \(DMEA\) là hình vuông 

⟹ \(AM\) là tia phân giác của \(\widehat{BAC}\)

Xét \( \triangle ABC \) có \(AM\) là đường trung tuyến, \(AM\) là đường phân giác của \( \triangle ABC \)

⟹ \( \triangle ABC \) cân tại \( A \) mà \(\widehat{BAC}=90^\circ\)

⟹ \( \triangle ABC \) vuông cân tại \( A \)

Vậy để \( DMEA \) là hình vuông, \( \triangle ABC \) cần thêm điều kiện là \( \triangle ABC \) vuông cân tại \( A \).

---

Câu 9 (Trường THCS Chương Dương – Hà Nội)

Cho \( \triangle ABC \) cân tại A (\( \widehat{A} < 90^\circ \)). Kẻ \( BE \perp AC \) tại \( E \) và \( CD \perp AB \) tại \( D \).

a) Chứng minh \( BE = CD \).

b) Chứng minh tứ giác \( BDEC \) là hình thang cân.

c) Gọi \( I \) là giao điểm của \( BE \) và \( CD \), tìm điều kiện của \( \triangle ABC \) để \( I \) cách đều 3 cạnh của \( \triangle ABC \) và khi đó chứng minh \( BD = DE = EC \).

Hướng dẫn:

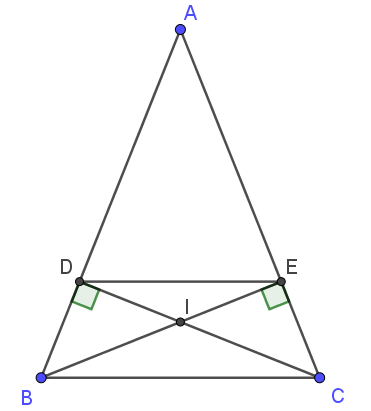
a) Có \( \triangle ABC \) cân tại \( A \) (gt) ⟹ \( AB = AC \); \( \widehat{ABC} = \widehat{ACB} \) (tính chất tam giác cân)

Xét \( \triangle BDC \) và \( \triangle BEC \) có:

BC chung

\( \widehat{DBC} = \widehat{BCE} \)

\( \widehat{BDC} = \widehat{BEC} = 90^\circ \) (do \( CD \perp AB \); \( BE \perp AC \))

⟹ \( \triangle BDC = \triangle CEB \) (cạnh huyền – góc nhọn)
⟹ \( BD = CE \); \( BE = CD \) (hai cạnh tương ứng).

b) Có \( AB -BD = AC - CE \) ⟹ \( AD = AE \).

Xét \( \triangle ADE \) có \( AD = AE \) (gt) ⟹ \( \triangle ADE \) cân tại \( A \) (định nghĩa)
⟹ \( \widehat{ADE} = \widehat{AED} \) (tính chất tam giác cân)

Có \( \widehat{ADE}+\widehat{AED} + \widehat{BAC} = 180^\circ \) ⟹ \( 2\widehat{ADE} + \widehat{BAC} = 180^\circ \) ⟹ \( \widehat{ADE} = \dfrac{180^\circ - \widehat{BAC}}{2} \)

Có \( \widehat{ABC} + \widehat{BCA} + \widehat{BAC} = 180^\circ \) ⟹ \( 2\widehat{ABC} + \widehat{BAC} = 180^\circ \) ⟹ \( \widehat{ABC} = \dfrac{180^\circ - \widehat{BAC}}{2} \)

⟹ \( \widehat{ABC} = \widehat{ADE} \) mà \( \widehat{ABC} \) và \( \widehat{ADE} \) ở vị trí đồng vị ⟹ \( BC \parallel DE \) ⟹ \( BDEC \) là hình thang.

Lại có \( \widehat{ABC} = \widehat{ACB} \) ⟹ \( BDEC \) là hình thang cân.

c) Giả sử \( I \) cách đều ba cạnh của \( \triangle ABC \).

⟹ \( I \) là giao của ba đường phân giác trong của \( \triangle ABC \).
⟹ \( CI \) là tia phân giác của \( \widehat{BCA} \).

Xét \( \triangle ACB \) có \( CD \) là đường cao, \( CD \) cũng là đường phân giác trong của \( \triangle ACB \).

⟹ \( \triangle ABC \) cân tại \( C \) ⟹ \( \widehat{BAC} = \widehat{ABC} \) mà \( \widehat{ABC} = \widehat{ACB} \)

⟹ \( \widehat{BAC} = \widehat{ABC} = \widehat{ACB} \) ⟹ \( \triangle ABC \) đều.

⟹ \( \widehat{BAC} = 60^\circ \) mà \( \triangle ADE \) cân tại \( A \) ⟹ \( \triangle ADE \) đều ⟹ \( AD = DE = EA \).

Mà \( AD = DB \); \( CE = EA \) (do \( \triangle ABC \) đều; \( CD \perp AB \); \( BE \perp AC \))

⟹ \( BD = DE = EA \).

Vậy \( \triangle ABC \) đều thì điểm \( I \) cách đều ba cạnh của \( \triangle ABC \), khi đó \( BD = DE = EA \).

---

Câu 10 (Trường THCS Văn Quán – Hà Nội)

Cho tam giác MNP nhọn có \( MN < MP \). Lấy điểm A trên cạnh MP (A khác M và P), từ A kẻ đường thẳng song song với NP cắt MN tại B, từ A kẻ đường thẳng song song với MN cắt NP tại C.

a) Chứng minh tứ giác ABNC là hình bình hành.
b) Từ B kẻ \( BH \perp AN \), từ C kẻ \( CK \perp AN \) (I, K thuộc AN). Chứng minh \( BH = CK \).
c) Kéo dài BH cắt NP tại I, kéo dài CK cắt AB tại G, BC cắt HK tại O. Chứng minh G, O, I thẳng hàng.

Hướng dẫn

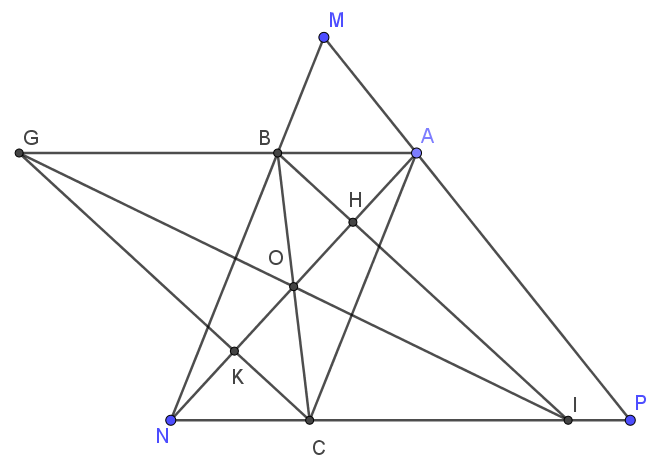
a) Xét tứ giác ABNC có \( AB // NC \), \( AC // BN \) (gt)
\( \Rightarrow \) ABNC là hình bình hành (dấu hiệu nhận biết).

b) Có ABNC là hình bình hành

\( \Rightarrow AB = CN \), \( AB // CN \) mà \( \widehat{ CNA}\) và \( \widehat{ BAN } \)ở vị trí so le trong

\( \Rightarrow \widehat{CNA} = \widehat{BAN} \).

Xét \( \triangle ABH \) và \( \triangle NCK \) có:

\(\widehat{CNK} = \widehat{BAH} \)
\( CN = AB \)
\(\widehat{ BHA }= \widehat{ CKN} = 90^\circ \) (do \( BH\perp AN; CK\perp AN\))
\( \Rightarrow \triangle ABH = \triangle NCK \) (cạnh huyền - góc nhọn)
\( \Rightarrow BH = CK \) (hai cạnh tương ứng)

c) Có \( BH \perp AN; CK \perp AN \Rightarrow BH // CK \)
Xét tứ giác GBIC: \( BI // CG \), \( BG // CI \) \( \Rightarrow GBIC \) là hình bình hành (dấu hiệu nhận biết).
\( \Rightarrow GI \) và BC cắt nhau tại trung điểm mỗi đoạn.
Mà O là trung điểm BC (do ABNC là hình bình hành)
\( \Rightarrow O \) cũng là trung điểm của \( GI \) \( \Rightarrow G, O, I \) thẳng hàng.