MỘT SỐ BÀI TOÁN VẬN DỤNG VỀ ĐỒ THỊ HÀM SỐ

MATHX gửi quý phụ huynh và các em học sinh một số bài toán vận dụng về đồ thị hàm số kèm đáp án chi tiết.

Bài 1. Trong mặt phẳng tọa độ Oxy, cho hàm số \( y = (a - 1)x + a \)

a) Tìm \( a \) để hàm số là hàm số bậc nhất.

b) Chứng minh rằng đồ thị hàm số luôn đi qua điểm \( A(-1;1) \)

c) Tìm \( a \) để đồ thị hàm số đi qua gốc tọa độ.

Hướng dẫn.

a) Để hàm số \( y = (a - 1)x + a \) (1) là hàm số bậc nhất thì \( a - 1 \neq 0 \) hay \( a \neq 1 \).

b) Thay \( x = -1 \) vào hàm số (1), ta có:

\( (a - 1)(-1) + a = 1 - a + a = 1 \)

Vậy đồ thị hàm số \( y = (a - 1)x + a \) luôn đi qua điểm \( A(-1;1) \).

c) Thay tọa độ \( O(0;0) \) vào hàm số (1), ta có:

\( (a - 1)\cdot 0 + a = 0 \Rightarrow a = 0 \)

Vậy \( a = 0 \) thì đồ thị hàm số đi qua gốc tọa độ.

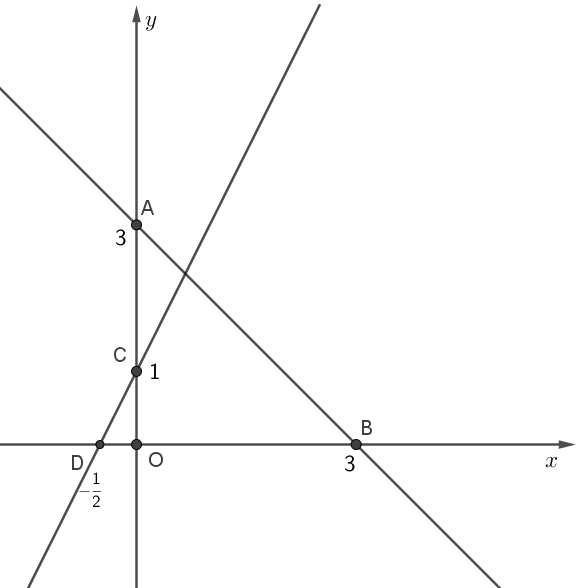
Bài 2. Vẽ đồ thị hàm số \( y = -x + 3 \), \( y = 2x + 1 \) trong cùng mặt phẳng tọa độ (Oxy)

Hướng dẫn.

* Vẽ đồ thị \( (d_1): y = -x + 3 \)

Cho \( x = 0 \Rightarrow y = 3 \) ⇒ Đường thẳng \( d_1 \) đi qua điểm \( A(0;3) \)

Cho \( y = 0 \Rightarrow -x + 3 = 0 \Rightarrow x = 3 \) ⇒ Đường thẳng \( d_1 \) đi qua điểm \( B(3;0) \)

* Vẽ đồ thị \( (d_2): y = 2x + 1 \)

Cho \( x = 0 \Rightarrow y = 1 \) ⇒ Đường thẳng \( d_2 \) đi qua điểm \( C(0;1) \)

Cho \( y = 0 \Rightarrow 2x + 1 = 0 \Rightarrow x = -\frac{1}{2} \) ⇒ Đường thẳng \( d_2 \) đi qua điểm \( D\left(-\frac{1}{2};0\right) \)

Bài 3. Xác định đường thẳng \( (d) \) trong mặt phẳng tọa độ \( (Oxy) \) biết nó có hệ số góc bằng \( 2 \) và đi qua điểm \( A(2;-3) \).

Hướng dẫn.

Gọi hàm số của đường thẳng \( (d) \) có dạng \( y = ax + b \).

Vì đường thẳng \( (d) \) có hệ số góc là \( 2 \) nên \( a = 2 \).

Khi đó hàm số của \( (d) \) có dạng \( y = 2x + b \).

Vì \( (d) \) đi qua điểm \( A(2;-3) \) nên \( -3 = 2 \cdot 2 + b \Rightarrow b = -7 \).

Vậy đường thẳng \( (d) \) là đồ thị của hàm số \( y = 2x - 7 \).

Bài 4. Cho hàm số \( y = (m - 1)x + 2m \). Xác định giá trị của \( m \) để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng \( 2 \).

Hướng dẫn.

Vì đồ thị hàm số cắt trục tung tại điểm có tung độ bằng \( 2 \) nên đồ thị hàm số đi qua điểm \( A(0;2) \).

Thay \( x = 0 \), \( y = 2 \) vào hàm số, ta có:

\( (m - 1)\cdot 0 + 2m = 2 \Rightarrow 2m = 2 \Rightarrow m = 1 \)

Vậy \( m = 1 \) thì đồ thị hàm số cắt trục tung tại điểm có tung độ bằng \( 2 \).

Bài 5. Cho hàm số \( y = (3m - 4)x + 5m \). Xác định giá trị của \( m \) để đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng \( 1 \).

Hướng dẫn.

Vì đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng \( 1 \) nên đồ thị hàm số đi qua điểm \( A(1;0) \).

Thay \( x = 1 \), \( y = 0 \) vào hàm số, ta có:

\( (3m - 4)\cdot 1 + 5m = 0 \Rightarrow 8m - 4 = 0 \Rightarrow m = \frac{1}{2} \)

Vậy \( m = \frac{1}{2} \) thì đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng \( 1 \).

Bài 6. Trong hệ trục tọa độ \( (Oxy) \), cho hai đồ thị hàm số \( y = 3x + 5 \) và \( y = -2x \).

Gọi \( A \) là giao điểm của hai đồ thị đó. Tìm tọa độ của \( A \).

Hướng dẫn.

Xét phương trình hoành độ giao điểm của hai đồ thị hàm số, ta có:

\( 3x + 5 = -2x \Rightarrow 5x + 5 = 0 \Rightarrow x = -1 \)

Thay \( x = -1 \) vào \( y = 3x + 5 \), ta có:

\( y = 3\cdot(-1) + 5 = 2 \)

Vậy tọa độ giao điểm của hai đồ thị là \( A(-1;2) \).

Bài 7. Trong hệ trục tọa độ \( (Oxy) \), cho đồ thị hàm số \( (d): y = -x + 3 \). Biết rằng đường thẳng \( d \) cắt trục hoành và trục tung lần lượt tại \( A \) và \( B \). Tính diện tích tam giác \( AOB \).

Hướng dẫn.

Cho \( x = 0 \Rightarrow y = 3 \) ⇒ Đường thẳng \( d \) đi qua điểm \( B(0;3) \).

Cho \( y = 0 \Rightarrow -x + 3 = 0 \Rightarrow x = 3 \) ⇒ Đường thẳng \( d \) đi qua điểm \( A(3;0) \).

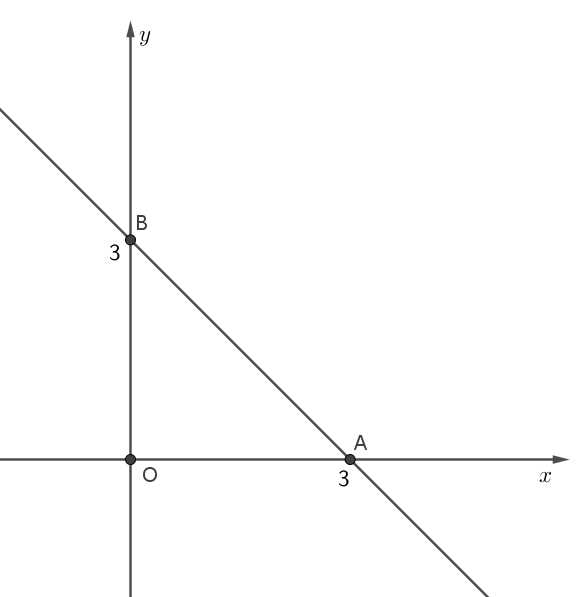
Diện tích tam giác \( OAB \) là: \( S_{\triangle OAB} = \frac{1}{2}\,OA \cdot OB = \frac{1}{2}\cdot 3 \cdot 3 = \frac{9}{2} \) (đơn vị diện tích).

Bài 8. Xác định đường thẳng đi qua hai điểm \( A(-2;2) \) và \( B(1;5) \).

Hướng dẫn.

Gọi hàm số của đường thẳng \( (d) \) có dạng \( y = ax + b \).

Vì \( (d) \) đi qua điểm \( A(-2;2) \) nên \( 2 = -2a + b \Rightarrow b = 2a + 2 \) (1).

Vì \( (d) \) đi qua điểm \( B(1;5) \) nên \( 5 = a + b \) (2).

Thay \( b = 2a + 2 \) vào (2), ta có:

\( a + 2a + 2 = 5 \Rightarrow 3a = 3 \Rightarrow a = 1 \).

Thay \( a = 1 \) vào (1), ta có: \( b = 2\cdot 1 + 2 = 4 \).

Vậy đường thẳng đi qua hai điểm \( A \) và \( B \) là đồ thị của hàm số \( y = x + 4 \).

Bài 9. Trong hệ trục tọa độ \( (Oxy) \), cho các điểm \( A(0;-5) \), \( B(1;-2) \), \( C(2;1) \). Chứng minh \( A, B, C \) thẳng hàng.

Hướng dẫn.

Gọi hàm số của đường thẳng \( (d) \) đi qua \( A, B \) có dạng \( y = ax + b \).

Vì \( (d) \) đi qua điểm \( A(0;-5) \) nên \( -5 = 0\cdot a + b \Rightarrow b = -5 \).

Vì \( (d) \) đi qua điểm \( B(1;-2) \) nên \( -2 = a + b \) (1).

Thay \( b = -5 \) vào (1), ta có:

\( a - 5 = -2 \Rightarrow a = 3 \).

Vậy đường thẳng \( d \) đi qua \( A, B \) là đồ thị của hàm số \( y = 3x - 5 \) (2).

Thay \( x = 2 \) vào (2), ta có:

\( y = 3\cdot 2 - 5 = 1 \) ⇒ \( d \) đi qua điểm \( C(2;1) \).

Vậy ba điểm \( A, B, C \) thẳng hàng.

Bài 10. Cho ba đường thẳng \( (d_1): y = x - 2 \), \( (d_2): y = 2x - 1 \), \( (d_3): y = -5x - 8 \). Chứng minh ba đường thẳng đồng quy.

Hướng dẫn.

Xét phương trình hoành độ giao điểm của đường thẳng \( (d_1) \) và \( (d_2) \), ta có:

\( x - 2 = 2x - 1 \Rightarrow x + 1 = 0 \Rightarrow x = -1 \)

Thay \( x = -1 \) vào \( y = x - 2 \), ta có:

\( y = -1 - 2 = -3 \)

Vậy đường thẳng \( (d_1) \) cắt đường thẳng \( (d_2) \) tại điểm \( A(-1;-3) \).

Thay \( x = -1 \) vào hàm số của đường thẳng \( (d_3) \), ta có:

\( y = -5\cdot(-1) - 8 = -3 \)

Vậy đường thẳng \( (d_3) \) đi qua điểm \( A(-1;-3) \).

Vậy ba đường thẳng \( (d_1), (d_2), (d_3) \) đồng quy tại điểm \( A(-1;-3) \).