MỘT SỐ CÂU HỎI HÌNH HỌC TRONG ĐỀ THI CUỐI KÌ I LỚP 8 CỦA CÁC TRƯỜNG (BỘ SÁCH: KẾT NỐI TRI THỨC VỚI CUỘC SỐNG)

MATHX gửi quý phụ huynh và các em học sinh một số câu hỏI hình học trong đề thi cuối kì I lớp 8 của các trường (bộ sách kết nối tri thức với cuộc sống) kèm đáp án chi tiết.

Câu 1. (Trường THCS Xuân Đài – Nam Định, năm 2024 – 2025)

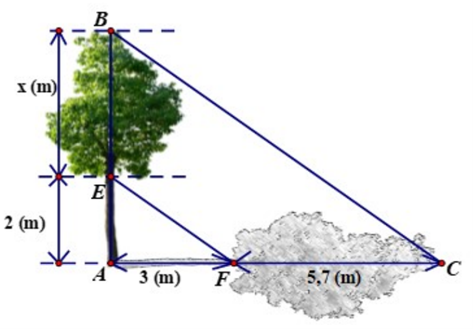
Vào một thời điểm trong ngày, bạn Nam quan sát được bóng của một cây trên mặt đất như hình vẽ. Biết rằng EF // BC. Em hãy giúp bạn Nam tính chiều cao của cây.

Hướng dẫn:

Có AC = AF + FC = 3 + 5,7 = 8,7 (m)

Xét △ABC có EF // BC ⇒ \( \dfrac{AE}{AB} = \dfrac{AF}{AC} \) (Định lý Thales)

Mà AE = 2 m, AF = 3 m, AC = 8,7 m:

\( \dfrac{2}{AB} = \dfrac{3}{8,7} \) ⇒ \( AB = \dfrac{2 \cdot 8,7}{3} = 5,8\,(m) \)

Vậy chiều cao của cây là 5,8 m.

Câu 2. (THCS Bình Lợi Trung – TP. Hồ Chí Minh, năm 2024 – 2025)

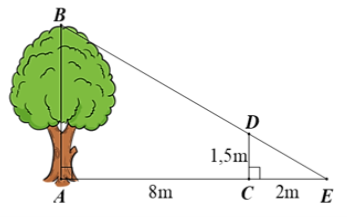
Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây (như hình vẽ). Biết cọc cao 1,5 m so với mặt đất, chân cọc cách gốc cây 8 m và cách bóng của đỉnh cọc 2 m. Tính chiều cao AB của cây?

Hướng dẫn:

Có AE = AC + CE = 8 + 2 = 10 (m)

Xét △ABE có CD // AB ⇒ \( \dfrac{CD}{AB} = \dfrac{CE}{AE} \) (Hệ quả của định lý Thales)

Mà CE = 2 m, AE = 10 m, CD = 1,5 m:

\( \dfrac{1,5}{AB} = \dfrac{2}{10} \) ⇒ \( AB = \dfrac{1,5 \cdot 10}{2} = 7,5\,(m) \)

Vậy chiều cao của cây là 7,5 m.

Câu 3 (Trường THCS Nguyễn Trãi – Quảng Nam, năm 2024 – 2025)

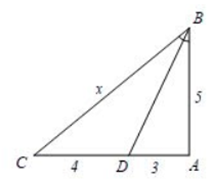
Cho hình vẽ, tìm số đo x?

Hướng dẫn:

Xét \( \triangle ABC \) có BD là phân giác của \( \widehat{ABC} \)

\( \dfrac{AD}{CD} = \dfrac{BA}{BC} \) (tính chất đường phân giác trong tam giác)

Mà CD = 4, AD = 3, AB = 5, BC = x nên

\( \dfrac{3}{4} = \dfrac{5}{x} \Rightarrow x = \dfrac{5 \cdot 4}{3} = \dfrac{20}{3} \)

Vậy \( x = \dfrac{20}{3} \)

Câu 4 (Trường THCS Phan Đình Giót – Hà Nội, năm 2024 – 2025)

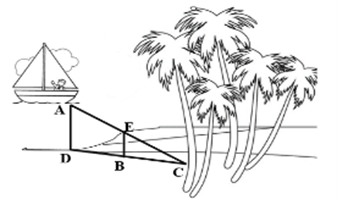
Cho hình vẽ, biết: BE // DA, EC = 9,6 m, DB = 4,5 m, BC = 5m. Một người đứng ở vị trí E trên bờ, tính khoảng cách AE từ chiếc thuyền tới vị trí người đứng?

Hướng dẫn:

Có CD = CB + BD = 5 + 4,5 = 9,5 m

Xét \( \Delta ACD \) có AD // EB ⇒ \( \dfrac{BC}{DC} = \dfrac{CE}{AC} \) (Định lý Thales)

Mà EC = 9,6 m, CD = 9,5 m, BC = 5 m

\( \Rightarrow \dfrac{5}{9,5} = \dfrac{9,6}{AC} \Rightarrow AC = \dfrac{9,6 \cdot 9,5}{5} = 18,24 \text{ m} \)

Vậy AE = AC – EC = 8,64 (m)

Vậy khoảng cách AE là 8,64 m

Câu 5 (Trường THCS Nguyễn Công Trứ – Hà Nội, năm 2024 – 2025)
Để đo khoảng cách giữa hai điểm A và B bị chắn ngang bởi một một vật cản, người ta đóng các cọc đo tại các vị trí như hình vẽ. Biết M, N lần lượt là các điểm chính giữa của các đoạn thẳng CA, CB và khoảng cách MN = 45 (m). Em hãy tính khoảng cách A và B.

Hướng dẫn:

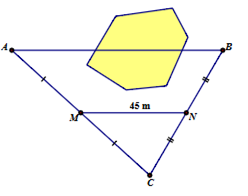
Xét \(\Delta ABC\) có AM = MC = \( \dfrac{1}{2}AC \); BN = NC = \( \dfrac{1}{2}BC \)
⇒ MN là đường trung bình của \(\Delta ABC\) (Định nghĩa)
⇒ MN = \( \dfrac{1}{2}AB \) ⇒ AB = 2MN mà MN = 45 m ⇒ AB = 2.45 = 90 (m)
Vậy khoảng cách A và B là 90 m.

Câu 6 (Trường THCS Lý Sơn – Hà Nội, năm 2024 – 2025)
Cho tam giác ABC nhọn. Vẽ tia phân giác của góc ACB cắt AB tại D.
1. Biết AC = 6cm, BC = 4cm, AD = 3cm. Tính DB.
2. Lấy điểm E đối xứng với điểm B qua điểm C. Từ D kẻ đường thẳng song song với BC cắt AC, AE lần lượt tại I, K.
Chứng minh: I là trung điểm của DK và CK vuông góc với CD.

Hướng dẫn:

a) Xét \(\Delta ABC\) có CD là phân giác của góc \(\widehat{BCA}\)
\( \dfrac{AD}{BD} = \dfrac{AC}{BC} \) mà AC = 6 cm, BC = 4 cm, AD = 3 cm.
⇒ \( \dfrac{3}{BD} = \dfrac{6}{4} \) ⇒ BD = \( \dfrac{3·4}{6} = 2 \text{ (cm)} \)
Vậy BD = 2 cm.

b) Xét \(\Delta ABC\) có DI // BC ⇒ \( \dfrac{DI}{BC} = \dfrac{AI}{AC} \) (Hệ quả của định lý Thales)

Xét \(\Delta ACE\) có IK // CE ⇒ \( \dfrac{IK}{CE} = \dfrac{AI}{AC} \) (Hệ quả của định lý Thales)

Mà \( \dfrac{DI}{BC} = \dfrac{AI}{AC} \Rightarrow \dfrac{DI}{BC} = \dfrac{IK}{CE} = \left( \dfrac{AI}{AC} \right) \) mà BC = CE ⇒ DI = IK.

Mà I nằm giữa D và K nên I là trung điểm của DK.

Xét \(\Delta ABE\) có DK // BE ⇒ \( \dfrac{AK}{KE} = \dfrac{AD}{BD} \) (Định lý Thales)

⇒\( \dfrac{AK}{KE} = \dfrac{AD}{BD} \) mà \( \dfrac{AD}{BD} = \dfrac{AC}{BC} \Rightarrow \dfrac{AK}{KE} = \dfrac{AC}{BC} \left(= \dfrac{AD}{BD} \right) \) mà BC = CE.

⇒ \( \dfrac{AK}{KE} = \dfrac{AC}{CE} \) ⇒ CK là đường phân giác trong \(\Delta ACE\).

⇒ \( \widehat{ ACK} = \dfrac{1}{2} \widehat{ ACE} \) mà \( \widehat{ DCI} = \dfrac{1}{2} \widehat{ BCE }\) ⇒ \( \widehat{ DCA }+ \widehat{ ACK }= \dfrac{1}{2} ( \widehat{ ACE }+ \widehat{ BCA}) \)

⇒ \( \widehat{ DCK }= \dfrac{1}{2} \cdot 180^\circ = 90^\circ \) ⇒ CK ⟂ CD.

Câu 7 (Trường THCS Thuận Thiên – Hải Phòng, năm 2024 – 2025)
Cho tam giác ABC cân tại A, đường cao AH. Gọi N là trung điểm của AC, K đối xứng với H qua N.

a) Chứng minh tứ giác AHCK là hình chữ nhật.

b) BK cắt AH tại O, CA cắt AI tại I. Chứng minh BC = 4·NO.

Hướng dẫn:

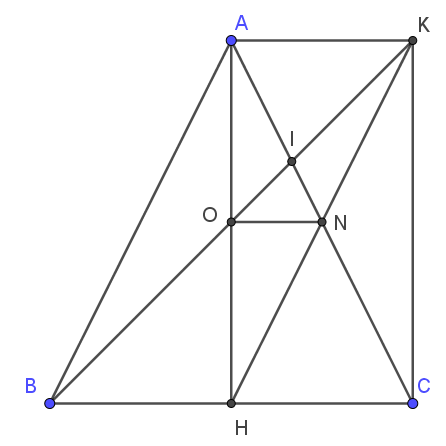
a) Xét tứ giác AHCK có \( AN = NC = \dfrac{1}{2}AC \), \( HN = NK = \dfrac{1}{2}HK \)
⇒ AHCK là hình bình hành (Dấu hiệu nhận biết).
Mà \( \widehat {AHC} = 90^\circ \) (do AH ⟂ BC) ⇒ AHKC là hình chữ nhật (Dấu hiệu nhận biết).

b) Xét \(\Delta ABC\) cân tại A có AH là đường cao
⇒ AH đồng thời là đường trung tuyến của tam giác ⇒ \( BH = HC \)
Có AKCH là hình chữ nhật.

⇒ \( AK // HC \), \( AN = NC = \dfrac{1}{2}AC \), AK = HC (tính chất hình chữ nhật).

Mà HC = BK ⇒ AK = BH (= HC).
Xét tứ giác AKHB có AK // BH, AK = BH ⇒ AKHB là hình bình hành.

⇒ \( AO = OH = \dfrac{1}{2}AH \)

Xét \(\Delta AHC\) có \( AO = OH = \dfrac{1}{2}AH \), \( AN = NC = \dfrac{1}{2}AC \)
⇒ ON là đường trung bình của tam giác AHC.

⇒ \( HC = 2ON \) mà \( HC = \dfrac{1}{2}BC \) ⇒ \( \dfrac{1}{2}BC = 2ON \) ⇒ \( BC = 4ON \)

Câu 8. (Trường THCS Ngô Gia Tự – Hải Phòng, năm 2023 – 2024)
Cho hình thang ABCD (AB // CD, CD = 2AB). Gọi E là trung điểm của CD.

a) Chứng minh tứ giác ABED là hình bình hành.

b) Từ điểm M trên cạnh AD (M ≠ A, M ≠ D) kẻ đường thẳng song song với hai đáy cắt các đoạn thẳng AC, BC theo thứ tự tại I, N. Chứng minh rằng: \( AM \cdot NC = BN \cdot MD \)

Hướng dẫn:

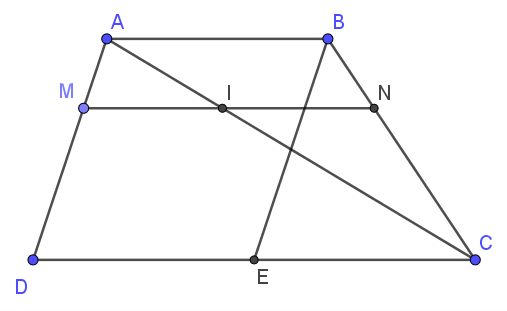
a) Có ABCD là hình thang ⇒ AB // CD

Có CD = 2AB ⇒ AB = \( \dfrac{1}{2}CD \) mà DE = \( \dfrac{1}{2}CD \) (Vì E là trung điểm của CD)
⇒ AB = DE.

Xét tứ giác ABED có AB // DE, AB = DE
⇒ ABED là hình bình hành (Dấu hiệu nhận biết).

b) Xét tam giác ABC có IN // BC ⇒ \( \dfrac{NC}{BC} = \dfrac{IC}{AC} \) (Định lý Thales) ⇒ \( \dfrac{NC}{BN} = \dfrac{IC}{AI} \)

Xét tam giác ADC có IM // DC ⇒ \( \dfrac{AM}{AD} = \dfrac{AI}{AC} \) (Định lý Thales) ⇒ \( \dfrac{DM}{AM} = \dfrac{IC}{AI} \)

Mà \( \dfrac{NC}{BN} = \dfrac{IC}{AI} \Rightarrow \dfrac{DM}{AM} = \dfrac{NC}{BN}\left(= \dfrac{IC}{AI}\right)\)
⇒ AM·NC = DM·BN.

Câu 9. (Trường THCS Thanh Quan – Hà Nội, năm 2023 – 2024)
Cho tam giác ABC vuông tại B (BC > BA), với M là trung điểm của AC. Từ M kẻ ME vuông góc với BC (E ∈ BC), MD vuông góc với AB (D ∈ AB).

a) Chứng minh tứ giác BDME là hình chữ nhật.

b) Lấy điểm F thuộc tia đối của ME sao cho MF = ME. Chứng minh: BE = EC và tứ giác AFCE là hình bình hành.

c) Gọi I, K lần lượt là giao điểm của BM, BF với AE. Tính \( \dfrac{IK}{FC} \)?

Hướng dẫn:

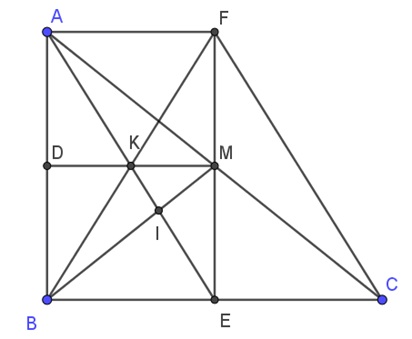
a) Có ME ⟂ BC, MD ⟂ AB ⇒ \(\widehat{MDB}=\widehat{MEB}=90^\circ\)
Xét tứ giác BDME có \(\widehat{MDB}=\widehat{MEB}=\widehat{DBE}=90^\circ\)
⇒ BDME là hình chữ nhật (Dấu hiệu nhận biết).

b) Xét tứ giác AFCE có \( AM = MC = \dfrac{1}{2}AC \), \( FM = ME = \dfrac{1}{2}FE \)
⇒ AFCE là hình bình hành (Dấu hiệu nhận biết).

Xét \(\Delta ABC\) có \( AM = MC = \dfrac{1}{2}AC \), ME // AB (do cùng vuông góc với BC)
⇒ BE = EC = \( \dfrac{1}{2}BC \) (tính chất đường trung bình của tam giác).

c) Xét \(\Delta BFE\) có BK = KF = \( \dfrac{1}{2}BF \) (do AFBE là hình chữ nhật); FM = ME = \( \dfrac{1}{2}FE \) (Do AFCE là hình bình hành). EK ∩ BM = {I}.

⇒ I là trọng tâm của \(\Delta BFE\) ⇒ \( \dfrac{KI}{KE} = \dfrac{1}{3} \)

Xét \(\Delta BFC\) có K là trung điểm của BF, E là trung điểm của BC
⇒ KE là đường trung bình của \(\Delta BFC\).

⇒ \( \dfrac{KE}{FC} = \dfrac{1}{2} \) mà \( \dfrac{KI}{KE} = \dfrac{1}{3} \)
⇒ \( \dfrac{KI}{FC} = \dfrac{1}{2} \cdot \dfrac{1}{3} = \dfrac{1}{6} \)

Câu 10. (Trường THCS Giảng Võ 2 – Hà Nội, năm 2024 – 2025)
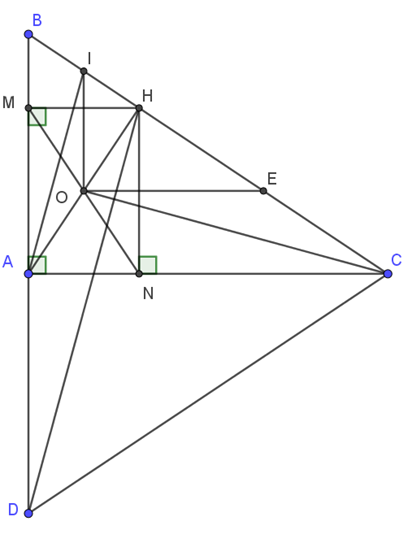
Cho \(\Delta ABC\) vuông tại A, đường cao AH. Từ H kẻ HM vuông góc với AB tại M, HN vuông góc với AC tại N. Gọi O là giao điểm của AH và MN.

1) Chứng minh \( \dfrac{AN}{NC} = \dfrac{BH}{HC} \)

2) Đường thẳng qua O song song với AC cắt BC tại E, đường thẳng qua O song song với AB cắt BC tại I. Chứng minh E là trung điểm của HC và tính độ dài IE, biết BC = 15 cm.

3) Vẽ điểm D sao cho A là trung điểm của BD. Chứng minh HD ⟂ OC.

Hướng dẫn:

a) Có \( HN \perp AC \), \( HM \perp AB \)  \(\Rightarrow \widehat{HMA} = \widehat{HNA} = 90^\circ \)

Xét tứ giác AMHN có \( \widehat{HMA} = \widehat{MAN} = \widehat{HNA} = 90^\circ \)

\(\Rightarrow\) AMHN là hình chữ nhật.

⇒ \( HN \parallel AM \), \( OA = OH = OM = ON = \frac{1}{2} AH \)

Xét \( \Delta ABC \) có \( HN \parallel AB \)  \( \Rightarrow \frac{NC}{AC} = \frac{HC}{BC} \Rightarrow \frac{AN}{NC} = \frac{BH}{HC} \)

b) Xét \( \Delta ABH \) có \( AO = OH = \frac{1}{2} AH \), \( OI \parallel AB \)

⇒ \( BI = IH = \frac{1}{2} BH \) (tính chất đường trung bình của tam giác)

Xét \( \Delta AHC \) có \( AO = OH = \frac{1}{2} AH \), \( OE \parallel AC \)

⇒ \( CE = EH = \frac{1}{2} CH \) (tính chất đường trung bình của tam giác)

⇒ \( IE = IH + HE = \frac{1}{2} BH + \frac{1}{2} HC = \frac{1}{2}(BH + HC) = \frac{1}{2} BC = \frac{15}{2} \) (cm)

c) Xét \( \Delta BHD \) có \( BI = IH = \frac{1}{2} BH \), \( BA = AD = \frac{1}{2} AD \)

⇒ AI là đường trung bình của \( \Delta BDH \Rightarrow\)  \( AI \parallel DH \)

Có \( OI \parallel AB \), \( AB \perp AC \Rightarrow OI \perp AC \) 

Xét \( \Delta AIC \) có \( OI \perp AC \), \( AH \perp IC \). \( AH \cap IO = \{ O \} \Rightarrow\)  O là trực tâm của \( \Delta AIC \)

⇒ \( OC \perp AI \). Mà \( AI \parallel DH \Rightarrow OC\perp DH\)