
Đội ngũ MATHX.VN biên soạn Tổng hợp 5 ĐỀ THI HK2 TOÁN 7 có đáp án và lời giải chi tiết của các bộ sách mới Kết nối tri thức, Cánh diều, Chân trời sáng tạo, giúp các em học sinh luyện thi hiệu quả.
Phụ huynh và các em học sinh xem thêm bộ 5 đề thi học kì 2 toán lớp 7 kèm lời giải chi tiết tại đây:
TỔNG HỢP ĐỀ THI HỌC KỲ 2 MÔN TOÁN LỚP 7 2024 KÈM LỜI GIẢI - ĐỀ 1
TỔNG HỢP ĐỀ THI HỌC KỲ 2 MÔN TOÁN LỚP 7 2024 KÈM LỜI GIẢI - ĐỀ 2
TỔNG HỢP ĐỀ THI HỌC KỲ 2 MÔN TOÁN LỚP 7 2024 KÈM LỜI GIẢI - ĐỀ 3
TỔNG HỢP ĐỀ THI HỌC KỲ 2 MÔN TOÁN LỚP 7 2024 KÈM LỜI GIẢI - ĐỀ 4
TỔNG HỢP ĐỀ THI HỌC KỲ 2 MÔN TOÁN LỚP 7 2024 KÈM LỜI GIẢI - ĐỀ 5
Bài 1. (1 điểm) Tìm x biết:
a) \(-0,1:x=-0,2:0,06\)
b) \({\dfrac{2-x}{4}}={\dfrac{3x-1}{3}}\)
Lời giải:
a) \(-0,1:x=-0,2:0,06\)
\({\dfrac{-0,1}{x}}={\dfrac{-0,2}{0,06}}\)
\({\dfrac{-0,1}{x}}={\dfrac{-1}{5}}:{\dfrac{3}{50}}\)
\({\dfrac{-0,1}{x}}={\dfrac{-1}{5}}.{\dfrac{50}{3}}\)
\({\dfrac{-0,1}{x}}={\dfrac{-10}{3}}\)
Áp dụng tính chất tỉ lệ thức ta có:
\(-0,1.3=-10x\)
-0,3 = -10x
\(x=-0,3:(-10)\)
\(x={\dfrac{-3}{10}}.\left({\dfrac{1}{-10}}\right)\)
\(x={\dfrac{3}{100}}\)
Vậy \(x={\dfrac{3}{100}}\)
b) \({\dfrac{2-x}{4}}={\dfrac{3x-1}{3}}\)
\(3\left(2-x\right)=4\left(3x-1\right)\)
\(6-3x=12x-4\)
\(-3x-12x=-4-6\)
\(-15x=-10\)
\(x={\dfrac{2}{3}}\)
Vậy \(x={\dfrac{2}{3}}\)
Bài 2. (1,5 điểm) Ba đơn vị kinh doanh A, B và C góp vốn theo tỉ lệ 2 : 3 : 7 sau một năm thu được tổng cộng 960 triệu đồng tiền lãi. Hỏi mỗi đơn vị được chia bao nhiêu tiền lãi biết tiền lãi được chia tỉ lệ thuận với số vốn đã góp.
Lời giải:
Gọi số tiền lãi của ba đơn vị kinh doanh A, B và C lần lượt là x, y, z (triệu đồng) (điều kiện: x, y, z > 0)
Theo bài ra, ta có: \(\left\{ \begin{array}{} {\dfrac{x}{2}}={\dfrac{y}{3}}={\dfrac{z}{7}} \\ x+y+z=960 \\ \end{array} \right.\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\({\dfrac{x}{2}}={\dfrac{y}{3}}={\dfrac{z}{7}}={\dfrac{x+y+z}{2+3+7}}={\dfrac{960}{12}}=80\)
Khi đó, \({\dfrac{x}{2}}=80\Rightarrow x=160\) (tmđk)
\({\dfrac{y}{3}}=80\Rightarrow x=240\) (tmđk)
\({\dfrac{z}{7}}=80\Rightarrow x=560\) (tmđk)
Vậy số tiền lãi của ba đơn vị kinh doanh là: Đơn vị A: 160 triệu đồng, đơn vị B: 240 triệu đồng, đơn vị C: 560 triệu đồng.
Bài 3. (2 điểm)
Cho các đa thức:
\(F\left(x\right)=5x^{2}-1+3x+x^{2}-5x^{3}\)
\(G\left(x\right)=2-3x^{3}+6x^{2}+5x-2x^{3}-x\)
a) Thu gọn và sắp xếp hai đa thức F(x) và G(x) theo lũy thừa giảm dần của biến.
b) Tính \(M\left(x\right)=F\left(x\right)-G\left(x\right);\) Tìm nghiệm của đa thức M (x)
c) Tìm đa thức \(N\left(x\right)+F\left(x\right)=-G\left(x\right)\)
Lời giải:
a) Thu gọn và sắp xếp theo lũy thừa giảm dần của biến.
Thu gọn F(x):
\(F\left(x\right)=5x^{2}-1+3x+x^{2}-5x^{3}\)
\(F\left(x\right)=-5x^{3}+\left(5x^{2}+x^{2}\right)+3x-1\)
\(F\left(x\right)=-5x^{3}+6x^{2}+3x-1\)
Thu gọn G(x):
\(G\left(x\right)=2-3x^{3}+6x^{2}+5x-2x^{3}-x\)
\(G\left(x\right)=\left(-3x^{3}-2x^{3}\right)+6x^{2}+\left(5x-x\right)+2\)
\(G\left(x\right)=-5x^{3}+6x^{2}+4x+2\)
b) Tính M(x):
\(M\left(x\right)=F\left(x\right)-G\left(x\right)\)
\(M\left(x\right)=\left(-5x^{3}+6x^{2}+3x-1\right)-\left(-5x^{3}+6x^{2}+4x+2\right)\)
\(M\left(x\right)=-5x^{3}+6x^{2}+3x-1+5x^{3}-6x^{2}-4x-2\)
\(M\left(x\right)=\left(-5x^{3}+5x^{3}\right)+\left(6x^{2}-6x^{2}\right)+\left(3x-4x\right)+(-1-2)\)
\(M\left(x\right)=-x-3\)
Tìm nghiệm của đa thức M(x):
Ta có: \(M\left(x\right)=-x-3=0\Leftrightarrow x=-3\)
Vậy x = − 3 là nghiệm của đa thức M(x).
c) Ta có:
\(N\left(x\right)+F\left(x\right)=-G\left(x\right)\)
\(\Rightarrow N\left(x\right)=-F\left(x\right)-G\left(x\right)=-\left[F\left(x\right)+G\left(x\right)\right]\)
Trong đó:
\(F\left(x\right)=-5x^{3}+6x^{2}+3x-1\)
\(G\left(x\right)=-5x^{3}+6x^{2}+4x+2\)
\(\Rightarrow F\left(x\right)+G\left(x\right)\)
\(=\left(-5x^{3}+6x^{2}+3x-1\right)+\left(-5x^{3}+6x^{2}+4x+2\right)\)
\(=-10x^{3}+12x^{2}+7x+1\)
\(\Rightarrow N\left(x\right)=-\left[F\left(x\right)+G\left(x\right)\right]\)
\(=-\left(-10x^{3}+12x^{2}+7x+1\right)\)
\(=10x^{3}-12x^{2}-7x-1\)
Vậy \(N\left(x\right)=10x^{3}-12x^{2}-7x-1.\)
Bài 4. (3 điểm) Cho tam giácABCvuông tạiAvà có đường phân giác BD. Kẻ đường thẳng DH vuông có với BCtại điểm H. Trên tia đối của tia AB lấy điểm K sao cho AK = CH.
a) Chứng minh rằng ΔABD = ΔHBD
b) Chứng minh rằng: Đường thẳng BD là đường trung trực của đoạn thẳng AH và AD < DC.
c) Chứng minh rằng: Ba điểm H,D,K thẳng hàng và đường thẳng BD vuông góc với đường thẳng KC.
d) Chứng minh rằng: \(2\left(A D+A K\right)\gt C K\)
Cho ΔABC cân tại A, tia phân giác của ∠BAC cắt cạnh BC tại D. Kẻ DH vuông góc với AB tại H, kẻ DK vuông.
Lời giải:
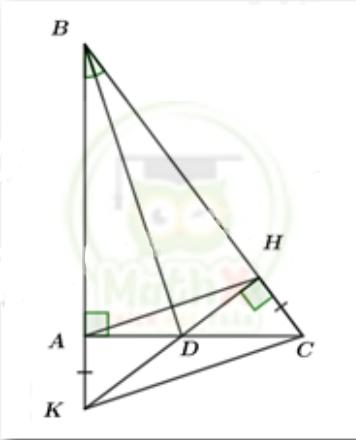
a) Xét ΔABD và ΔHBD có:
+ \(\angle A=\angle H=90^{\circ}\left(g t\right)\)
+ Cạnh BD chung.
+ \(\angle A B D=\angle H B D\left(g t\right)\)
=> \(\triangle A B D=\triangle H B D\) (cạnh huyền – góc nhọn) (đpcm).
b)
+ Do \(\Delta A B D=\Delta H B D\) => \(\left\{ \begin{array}{} AB = BH \\ AD = DH \\ \end{array} \right.\) là đường trung trực của AH (đpcm)
Ta có: AD = DH (1)
Mà ΔDHC vuông tại H => DH < DC (cạnh góc vuông < cạnh huyền (2)
Từ (1) và (2), suy ra AD < DC (đpcm)
c) * Chứng minh K, D, H thẳng hàng:
Xét ΔAKD và ΔHCD có:
\(A K=C H\left(\mathrm{gt}\right)\)
\(\angle A=\angle H=90^{\circ}\left(g t\right)\)
AD = DH (theo b)
=> \(\Delta A K D=\Delta H C D\left(c.g.c\right)\)
\(\Rightarrow\angle A D K=\angle H D C\) (hai góc tương ứng) (3)
Mặt khác \(\angle H D C+\angle H D A=\angle A D C=180^{\circ}\) (4)
Từ (3) và (4) \(\angle A K D+\angle H D A=180^{\circ}\)
=> DK, DH là hai tia đối nhau.
=> K, D, H thẳng hàng (đpcm)
* Chứng minh BD ⊥ KC
Xét ΔKBC có:
\(\left\{ \begin{array}{} KB = KA + AB \\ CB = CH + HB \\ \end{array} \right.\) Mà \(K A=C H;A B=H B\Rightarrow K B=C B.\)
=> ΔKBC cân tại B
Vì BD là tia phân giác của góc B nên suy ra BD đồng thời là đường cao trong ΔKBC ứng với cạnh KC.
=> BD ⊥ KC (đpcm)
d) Chứng minh rằng: \(2\left(A D+A K\right)\gt C K\)
Xét ΔAKD, ta có: \(A D+A K\gt K D\Rightarrow2\left(A D+A K\right)\gt 2K D\) (mối quan hệ giữa ba cạnh trong tam giác) (5)
Xét ΔKDC, ta có: KD = DC (do \(\Delta A K D=\Delta H C D\) ở cmt)
=> \(K D+D C\gt K C\)
⇔ 2KD > KC (6)
Từ (5) và (6) \(\Rightarrow2\left(A D+A K\right)\gt C K\) (đpcm)
Bài 5. (0,5 điểm) Cho đa thức \(f(x)\) thỏa mãn \(f\left(x\right)+x. f\left(-x\right)=x+1\) với mọi giá trị của x. Tính \(f(1)\)
Lời giải:
+ Với x = − 1, ta có: \(f\left(-1\right)+\left(-1\right). f\left(1\right)=-1+1\)
\(\Rightarrow f\left(-1\right)-f\left(1\right)=0\)
\(\Rightarrow f\,(-1)=f\,(1)\)
+ Với x = 1, ta có: \(f\left(1\right)+1.f\left(-1\right)=1+1\)
\(\Rightarrow f\left(1\right)+f\left(-1\right)=2\)
Suy ra, \(f\left(1\right)+f\left(1\right)=2\)
\(\Rightarrow2f\left(1\right)=2\)
\(\Rightarrow f\left(1\right)=1\)
Vậy \(\Rightarrow f\left(1\right)=1\)
Như vậy MATHX đã hướng dẫn các em giải chi tiết đề thi học kì 2 môn toán lớp 7 - đề số 3. Ngoài ra các bậc phụ huynh cần cho con em mình học đúng phương pháp và tham khảo các khóa học online tại MATHX.VN để giúp con tự tin chinh phục môn toán nhé.