
Để giúp các em ôn tập và nắm vững kiến thức, chuẩn bị tốt cho kỳ thi giữa kỳ sắp tới. Đội ngũ MATHX biên soạn bộ đề thi học kì 2 môn toán lớp 6 năm học 2024-2025, bao gồm 5 đề thi có đáp án và lời giải chi tiết bám sát cấu trúc của các trường, phòng, sở giáo dục trên cả nước. Chúc các em học tốt
Phụ huynh và các em học sinh xem thêm bộ 5 đề thi học kì 2 toán lớp 6 kèm lời giải chi tiết tại đây:
TỔNG HỢP ĐỀ THI HỌC KỲ 2 MÔN TOÁN LỚP 6 2024 KÈM LỜI GIẢI - ĐỀ 1
TỔNG HỢP ĐỀ THI HỌC KỲ 2 MÔN TOÁN LỚP 6 2024 KÈM LỜI GIẢI - ĐỀ 2
TỔNG HỢP ĐỀ THI HỌC KỲ 2 MÔN TOÁN LỚP 6 2024 KÈM LỜI GIẢI - ĐỀ 3
TỔNG HỢP ĐỀ THI HỌC KỲ 2 MÔN TOÁN LỚP 6 2024 KÈM LỜI GIẢI - ĐỀ 4
TỔNG HỢP ĐỀ THI HỌC KỲ 2 MÔN TOÁN LỚP 6 2024 KÈM LỜI GIẢI - ĐỀ 5
Bài 1 (1,5 điểm) Thực hiện phép tính (tính nhanh nếu có thể) :
a) \({\dfrac{7}{15}}+{\dfrac{6}{5}}\)
b) \(-\;1,8:{\biggl(}1-{\dfrac{7}{10}}{\biggr)}\)
c) \({\dfrac{-5}{7}}\cdot{\dfrac{2}{13}}+{\dfrac{-5}{7}}\cdot{\dfrac{3}{13}}-{\dfrac{5}{7}}\cdot{\dfrac{8}{13}}\)
Lời giải:
a) \({\dfrac{7}{15}}+{\dfrac{6}{5}}\)
\({\dfrac{7}{15}}+{\dfrac{6}{5}}={\dfrac{7}{15}}+{\dfrac{18}{15}}\)
= \({\dfrac{25}{15}}={\dfrac{5}{3}}\)
b) \(-\;1,8:{\biggl(}1-{\dfrac{7}{10}}{\biggr)}\)\(={\dfrac{-18}{10}}:{\dfrac{3}{10}}\)
\(={\dfrac{-18}{10}}\cdot{\dfrac{10}{3}}=-6\)
c) \({\dfrac{-5}{7}}\cdot{\dfrac{2}{13}}+{\dfrac{-5}{7}}\cdot{\dfrac{3}{13}}-{\dfrac{5}{7}}\cdot{\dfrac{8}{13}}\)
\(={\dfrac{-5}{7}}.\left({\dfrac{2}{13}}+{\dfrac{3}{13}}+{\dfrac{8}{13}}\right)\)
\(\textstyle={\dfrac{-5}{7}}\cdot1\)
\(\textstyle={\dfrac{-5}{7}}\)
Bài 2 (1 điểm) Tìm x biết :
a) \(x-1{\dfrac{2}{5}}={\dfrac{3}{4}}\)
b) \({\dfrac{1}{2}}x-{\dfrac{4}{7}}=1{\dfrac{3}{7}}\)
Lời giải:
a) \(x-1{\dfrac{2}{5}}={\dfrac{3}{4}}\)
\(x\ -\ {\dfrac{7}{5}}={\dfrac{3}{4}}\)
\(x\qquad={\dfrac{3}{4}}+{\dfrac{7}{5}}\)
\(\begin{array}{r l}{x}&{{}={\dfrac{43}{20}}}\end{array}\)
Vậy \({x}=\dfrac{43}{20}\)
b) \({\dfrac{1}{2}}x-{\dfrac{4}{7}}=1{\dfrac{3}{7}}\)
\({\dfrac{1}{2}}x-{\dfrac{4}{7}}={\dfrac{10}{7}}\)
\({\begin{array}{r l}{{\dfrac{1}{2}}x\quad}&{{}={\dfrac{10}{7}}+{\dfrac{4}{7}}}\end{array}}\,\)
\(\dfrac{1}{2}x= \dfrac{14}{7}\)
\(x={\dfrac{14}{7}}:{\dfrac{1}{2}}\)
x = 4
Vậy x = 4
Bài 3 (2 điểm) Trong một đợt lao động trồng cây, lớp 6A gồm ba tổ được phân công trồng 250 cây. Biết số cây tổ I trồng được bằng \(\dfrac{2}{5}\) tổng số cây cả lớp trồng và 30% số cây tổ II trồng được bằng 24 cây.
a) Tính số cây trồng được của tổ I và tổ II ;
b) Tính tỉ số phần trăm của số cây trồng được của tổ III so với số cây của cả lớp trồng.
Lời giải:
a) Số cây trồng được của tổ I là: \(250.{\dfrac{2}{5}}=100\) (cây)
Số cây trồng được của tổ II là:
24 : 30% = 24 : \(\dfrac{3}{10}\) = 80 (cây)
b) Số cây trồng được của tổ III là:
250 - (100 + 80) = 70 (cây)
Số cây trồng được của tổ III chiếm:
\(\dfrac{70.100}{250}\)% = 28% số cây trồng của cả lớp.
Bài 4 (3 điểm) Trên cùng một nửa mặt phẳng có bờ chứa tia Ox vẽ hai tia Oy, Oz sao cho ∠xOy = \(40^o\) và ∠xOz = \(80^o\)
a) Tính số đo ∠yOz
b) Chứng tỏ rằng tia Oy là tia phân giác của ∠xOz
c) Vẽ tia Ot là tia đối của tia đối của tia Ox. Tính số đo ∠yOt
d) Vẽ đường tròn tâm O, bán kính 3cm cắt đường thẳng xt tại hai điểm M, N. Trên tia Ox lấy điểm P sao cho OP = 4cm. Tính độ dài đoạn thẳng NP.
Lời giải:
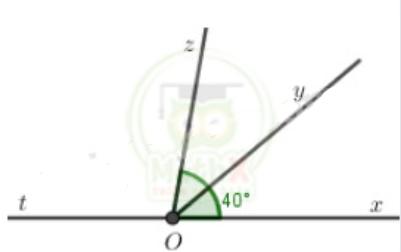
a) Trên mặt phẳng bờ chứa tia Ox ta có:
∠xOy < ∠xOz (\(40^o\) < \(80^o\))
=> Tia Oy nằm giữa hai tia Ox và Oz
=> ∠xOy + ∠yOz = ∠xOz
=> \(40^o\) + ∠yOz = \(80^o\)
=> ∠yOz = \(80^o\) - \(40^o\) = \(40^o\)
Vậy ∠yOz = \(40^o\)
b) Vì tia Oy nằm giữa hai tia Ox, Oz và ∠xOy = ∠yOz = \(40^o\)
=> Oy là tia phân giác của góc ∠xOz
c) Vì Ot là tia đối của tia Ox nên ∠xOt = \(180^o\)
=> Tia Oy nằm giữa hai tia Ox, Ot
=> ∠xOy + ∠yOt = ∠xOt
=> \(40^o\) + ∠yOt = \(180^o\)
=> ∠yOt = \(180^o\) - \(40^o\) = \(140^o\)
Vậy ∠yOt = \(140^o\)
d)
+ TH1: M ∈ tia Ot, N ∈ tia Ox
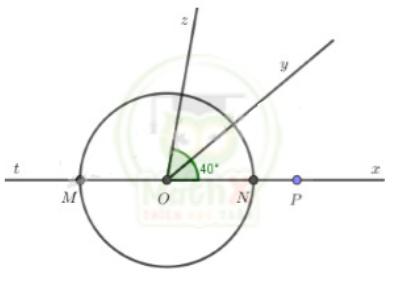
Ta có ON = 3cm, Om = 3cm (= bán kính đường tròn)
=> ON = 3cm < OP = 4cm
=> N nằm giữa hai điểm O và P
=> ON + NP = OP
=> 3 + NP = 4
=> NP = 4 - 3 = 1 (cm)
Vậy NP = 1cm
+ TH2: N ∈ tia Ot; M ∈ tia Ox
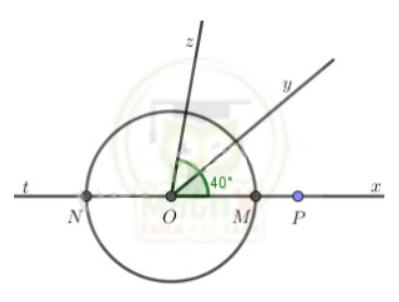
Ta có ON = 3 cm, OM = 3cm (= bán kính đường tròn)
Vì OM và ON là hai tia đối nhau, nên NM = NO + OM = 3 + 3 = 6 (cm)
Vì M nằm trên tia Ox, và OM < OP (3cm < 4cm)
=> M nằm giữa hai điểm O và P
=> OM + MP = OP
=> 3 + MP = 4
=> MP = 4 - 3 = 1 (cm)
Vì O nằm giữa N và M, M nằm giữa O và P nên M nằm giữa N và P
=> NM + MP = NP
6 + 1 = 7 (cm)
Vậy NP = 7cm
Bài 5 (0,5 điểm) Tính giá trị của biểu thức \(A={\dfrac{3}{2}}-{\dfrac{5}{6}}+{\dfrac{7}{12}}-{\dfrac{9}{20}}+{\dfrac{11}{12}}-{\dfrac{13}{12}}+{\dfrac{15}{56}}-{\dfrac{17}{72}}+{\dfrac{19}{90}}.\)
Lời giải:
Ta có: \(A={\dfrac{3}{2}}-{\dfrac{5}{6}}+{\dfrac{7}{12}}-{\dfrac{9}{20}}+{\dfrac{11}{12}}-{\dfrac{13}{12}}+{\dfrac{15}{56}}-{\dfrac{17}{72}}+{\dfrac{19}{90}}.\)
\(={\dfrac{3}{1.2}}-{\dfrac{5}{2.3}}+{\dfrac{7}{3.4}}-{\dfrac{9}{4.5}}+{\dfrac{11}{5.6}}-{\dfrac{13}{6.7}}+{\dfrac{15}{7.8}}-{\dfrac{17}{8.9}}+{\dfrac{19}{9.10}}\)
\(={\dfrac{3}{1}}-{\dfrac{3}{2}}-{\dfrac{5}{2}}+{\dfrac{5}{3}}+{\dfrac{7}{3}}-{\dfrac{7}{4}}-{\dfrac{9}{4}}+{\dfrac{9}{5}}+{\dfrac{11}{5}}\) - \({\dfrac{11}{6}}-{\dfrac{13}{6}}+{\dfrac{13}{7}}+{\dfrac{15}{7}}-{\dfrac{15}{8}}-{\dfrac{17}{8}}+{\dfrac{17}{9}}+{\dfrac{19}{9}}-{\dfrac{19}{10}}\)
\(=3+\left({\dfrac{-3}{2}}-{\dfrac{5}{2}}\right)+\left({\dfrac{5}{3}}+{\dfrac{7}{3}}\right)+\left(-{\dfrac{7}{4}}-{\dfrac{9}{4}}\right)+\left({\dfrac{9}{5}}+{\dfrac{11}{5}}\right)\) + \(\left(-{\dfrac{11}{6}}-{\dfrac{13}{6}}\right)+\left({\dfrac{13}{7}}+{\dfrac{15}{7}}\right)+\left(-{\dfrac{15}{8}}-{\frac{17}{8}}\right)+\left({\dfrac{17}{9}}+{\dfrac{19}{9}}\right)-{\dfrac{19}{10}}\)
\(=3-4+4-4+4-4+4-4+4-\dfrac{19}{10}\)
\(=3-{\dfrac{19}{10}}={\dfrac{11}{10}}\)
Trên đây MATHX đã hướng dẫn các em giải chi tiết đề thi học kì 2 môn toán lớp 6 - đề số 3. Ngoài ra các bậc phụ huynh cần cho con em mình học đúng phương pháp và tham khảo các khóa học online tại MATHX.VN để giúp con tự tin chinh phục môn toán nhé.