
Bộ 5 đề kiểm tra giữa kì 2 Toán 9 năm 2023 được MATHX biên soạn nhằm giúp học sinh ôn lại kiến thức và rèn kĩ năng giải bài tập để các em đạt kết quả cao hơn trong kì thi kiểm tra giữa kì 2 sắp tới. Chúc các em học tốt.
Phụ huynh và các em học sinh xem thêm đề thi giữa kì 2 môn toán lớp 9 năm học 2023 - 2024 tại đây:
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 1
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 2
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 3
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 4
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 5
Câu 1: Giải các hệ phương trình sau:
a) \(\left\{ \begin{array}{} 3 (x+1) - y = 6 - 2y \\ 2x - y = 7 \\ \end{array} \right.\)
b)
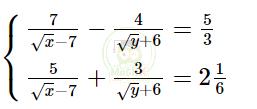
Lời giải:
Giải các hệ phương trình sau:
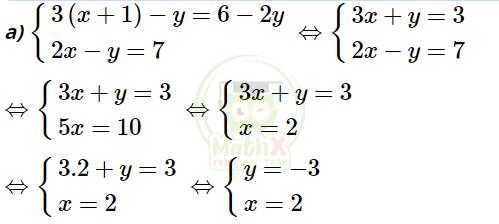
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (2; -3)
b)
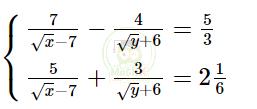
ĐKXĐ x, y ≥ 0, x ≠ 49
Đặt \(u=\dfrac{1}{\sqrt{x}-7}\) ; \(v=\dfrac{1}{\sqrt{y}+6}\) (u, v ≠ 0)
Khi đó, ta có hệ phương trình:
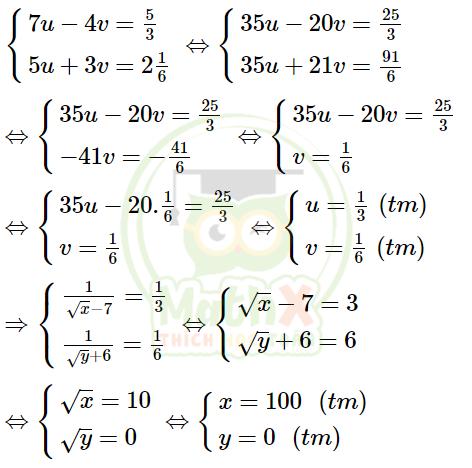
Vậy hệ phương trình có nghiệm duy nhất là (x; y) = (100; 0)
Câu 2: Giải bài toán bằng cách lập cách lập phương trình hoặc lập hệ phương trình
Hai tổ sản xuất trong tháng thứ nhất làm được 1000 sản phẩm. Sang tháng thứ hai, do cải tiến kĩ thuật nên tổ một vượt mức 20%, tổ hai vượt mức 15% so với tháng thứ nhất. Vì vậy, cả hai tổ sản xuất được 1170 sản phẩm. Hỏi tháng thứ nhất, mỗi tổ sản xuất được bao nhiêu sản phẩm?
Lời giải:
Gọi số sản phẩm tổ một sản xuất được trong tháng thứ nhất là x (sản phẩm, x ∈ N*, x < 1000)
Số sản phẩm tổ hai sản xuất được trong tháng thứ hai là y (sản phẩm, y ∈ N*, y < 1000)
Trong tháng thứ nhất cả hai tổ làm được 1000 sản phẩm nên ta có phương trình:
x + y = 1000 (1)
Số sản phẩm tổ một sản xuất được trong tháng thứ hai là
100%.x + 20%.x = 120%x (sản phẩm)
Số sản phẩm tổ hai sản xuất được trong tháng thứ hai là
100%.y + 15%.y = 115%y (sản phẩm)
Trong tháng thứ hai, cả hai tổ sản xuất được 1170 sản phẩm nên ta có phương trình:
120%x + 15%y = 1170
<=> 1,2x + 1,15y = 1170 (2)
Từ (1) và (2) ta có hệ phương trình:
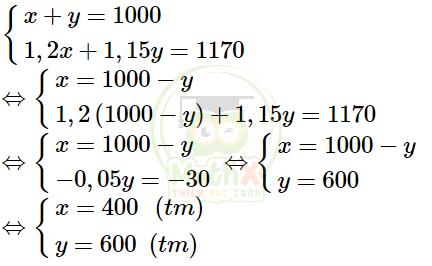
Vậy trong tháng thứ nhất tổ một sản phẩm được 400 sản phẩm, tổ hai sản xuất được 600 sản phẩm.
Câu 3: Cho đường thẳng (d) có phương trình y = ax + b. Tìm a, b biết (d) song song với đường thẳng (d') có phương trình y = -3x + 5 và đi qua điểm A thuộc parabol (P) có phương trình y = \(x^2\) có hoành độ bằng -2.
Lời giải:
Đường thẳng (d) có phương trình y = ax + b
Vì (d) song song với đường thẳng (d') : y = -3x + 5
nên a = -3 và b ≠ 5
Gọi \(A\left(x_{A};\;y_{A}\right)\in\left(P\right):y=x^{2}\,.\)
Ta có: \(x_{A}=-2\Rightarrow y_{A}=(-2)^{2}=4\)
=> A (-2: 4)
Vì đường thẳng (d) đi qua A (-2: 4) nên ta có:
4 = -2a + b (1)
Thay a = -3 vào (1) ta có:
4 = -2 . (-3) + b ⇔ b = -2 (thỏa mãn)
Vậy a = -3, b = -2.
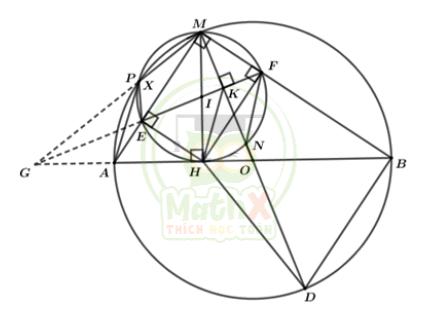
Câu 4: Cho đường tròn (O; R), kẻ đường kính AB. Điểm M bất kì trên (O) sao cho MA < MB (M ≠ A, B). Kẻ MH ⊥ AB tại H. Vẽ đường tròn (I) đường kính MH cắt MA, MB lần lượt tại E và F.
a) Chứng minh \(MH^2 = MF . MB\) và ba điểm E, I, F thẳng hàng.
b) Kẻ đường kính MD của đường tròn (O), MD cắt đường tròn (I) tại điểm thứ hai là N (N ≠ M). Chứng minh tứ giác BONF nội tiếp.
c) MD cắt EF tại K. Chứng minh MK ⊥ EF và ∠MHK = ∠MDH.
d) Đường tròn (I) cắt đường tròn (O) tại điểm thứ hai là P (P ≠ M). Chứng minh ba đường thẳng MP, FE và BA đồng quy
Lời giải:
a) Chứng minh \(MH^2 = MF . MB\) và ba điểm E, I, F thẳng hàng.
- Chứng minh \(MH^2 = MF . MB\)
Vì F thuộc đường tròn (I) đường kính MH nên ∠MFH = \(90^o\) (góc nội tiếp chắn nửa đường tròn)
=> HF ⊥ MB tại F
∠MHB = \(90^o\) (vì MH ⊥ AB tại H)
Xét ΔMHB vuông tại H đường cao HF, áp dụng hệ thức về cạnh và đường cao ta có:
\(MH^2 = MF . MB\) (đpcm)
- Chứng minh E, I, F thẳng hàng.
Xét tứ giác MEHF ta có:
∠AMB = \(90^o\) (góc nội tiếp chắn nửa đường tròn tâm O, đường kính AB)
∠HEM= \(90^o\) (góc nội tiếp chắn nửa đường tròn tâm I, đường kính AB)
∠HFM = \(90^o\) (góc nội tiếp chắn nửa đường tròn tâm I, đường kính MH)
=> ∠AMB = ∠HEM = ∠HFM = \(90^o\)
=> Tứ giác MEHF là hình chữ nhật (dấu hiệu nhận biết)
Mà I là trung điểm của MH (vì I là tâm của đường tròn đường kính MH) nên I là tâm của hình chữ nhật MEHF.
=> I là trung điểm của EF
=> Ba điểm E, I, F thẳng hàng (đpcm)
b) Kẻ đường kính MD của đường tròn (O), MD cắt đường tròn (I) tại điểm thứ hai là N (N ≠ M). Chứng minh tứ giác BONF nội tiếp.
Xét đường tròn (I) ta có: EF là đường trung trực của MN (liên hệ giữa đường kính và dây cung)
=> FM = FN
=> ΔMFN cân tại F (đn)
=> ∠FMN = ∠FNM (tc)
Xét đường tròn (O) ta có: OM = OB
=> ΔMOB cân tại O (đn)
=> ∠OMB = ∠OBM (tc)
Hay ∠FMN = ∠OBM
=> ∠FMN = ∠OBM (= ∠FMN)
⇒ Tứ giác BONF nội tiếp (Tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện) (đpcm)
c) MD cắt EF tại K. Chứng minh MK ⊥ EF và ∠MHK = ∠MDH.
Chứng minh MK ⊥ EF
Xét đường tròn (I), Ta có: ∠MEF = ∠MNF (góc nội tiếp cùng chắn cung)
Mà ∠MEF = ∠NMF (cmt)
=> ∠MEF = ∠NMF (= ∠MNF)
Ta có: ∠MEF = ∠MFE = \(90^o\) (vì tam giác MEF vuông tại M)
Mà ∠MEF = ∠NMF (cmt)
=> ∠NMF + ∠MFE = \(90^o\)
∠KMF + ∠MFK = \(90^o\)
Xét ΔMFK có ∠KMF + ∠MFK = \(90^o\) => ∠MFK = \(90^o\)
=> MK ⊥ EF tại K.
- Chứng minh ∠MHK = ∠MDH.
Xét ΔMFK và ΔMBD ta có:
góc M chung
∠MHK = ∠MBD (= \(90^o\))
=> ΔMFK ~ ΔMBD (g - g)
=> \({\dfrac{M K}{M B}}\,=\,{\dfrac{M F}{M D}}\) (cặp cạnh tương ứng tỉ lệ).
=> MK.MD = MF.MB
Theo câu a) ta có: \(MH^2 = MF . MB\)
=> \(MH^2 = MF . MB\) (= MF.MB)
=> MH.MH = MK.MD
=> \({\dfrac{M K}{M H}}\,=\,{\dfrac{M H}{M D}}\)
Xét ΔMKH và ΔMHD ta có:
\({\dfrac{M K}{M H}}\,=\,{\dfrac{M H}{M D}}\) (cmt)
góc M chung
=> ΔMKH ~ ΔMHD (c.g.c)
=> ∠MHK = ∠MDH (hai góc tương ứng)
d) Đường tròn (I) cắt đường tròn (O) tại điểm thứ hai là P (P ≠ M). Chứng minh ba đường thẳng MP, FE và BA đồng quy
Gọi G là giao điểm của EF và AB, X là giao điểm của MG và đường trong (O)
Ta có:
∠MEF + ∠MFE = \(90^o\) (vì ΔMEF vuông tại M)
∠MEF + ∠KMF = \(90^o\) (vì ΔMKF vuông tại K)
=> ∠MEF = ∠KMF (cùng phụ với ∠MFE)
Mà ∠KMF = ∠OBM (cmt)
=> ∠MEF = ∠OBM (= ∠KMF)
=> Tứ giác AEFB nội tiếp (Tứ giác có gộc ngoài bằng góc trong tại đỉnh đối diện)
=> ∠GEA = ∠GBF (góc ngoài của tứ giác bằng góc trong tại đỉnh đối diện)
Xét ΔGEA và ΔGBF ta có:
∠G chung
∠GEA = ∠GBF (cmt)
=> ΔGEA ~ ΔGBF (g.g)
=> \({\dfrac{GE}{GB}}\,=\,{\dfrac{GA}{GF}}\) (cặp cạnh tương ứng tỉ lệ)
=> GE.GF = GA.GB (1)
Tứ giác AXMB nội tiếp => ∠GXA = ∠GBM (góc ngoài của tứ giác bằng góc trong tại đỉnh đối diện)
Xét ΔGXA và ΔGBM có:
∠G chung
∠GXA = ∠GBM (cmt)
=> ΔGXA ~ ΔGBM
=> ΔGXA ~ ΔGBM (g.g)
=> \({\dfrac{GE}{GM}}\,=\,{\dfrac{GX}{GF}}\) (cặp cạnh tương ứng tỉ lệ)
Xét ΔGXE và ΔGFM ta có:
∠G chung
\({\dfrac{GE}{GM}}\,=\,{\dfrac{GX}{GF}}\) (cmt)
=> ΔGXE ~ ΔGFM (c.g.c)
=> ∠GXE = ∠GFM (hai góc tương ứng)
=> Tứ giác XMFE nội tiếp (Tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện) (1)
⇒ X là điểm nằm trên đường tròn (I) mà X cũng nằm trên trên đường tròn (O)
=> X là giao điểm của (I) và (O)
Theo đề bài, đường tròn (I) cắt đường tròn (O) tại điểm thứ hai là P (P ≠ M) suy ra X = P
Mà G,X,M là thẳng hàng suy ra G,P,M thẳng hàng.
=> Ba đường thẳng MP,FE và BA đồng quy tại G (đpcm)
Câu 5: Cho các số không âm x, y, z thỏa mãn x + y + z = 1. Tìm giá trị lớn nhất của biểu thức:
\(Q=\sqrt{2x^{2}+x+1}+\sqrt{2y^{2}+y+1}+\sqrt{2z^{2}+z+1}\)
Lời giải:
Vì x, y, z là các số không âm và x + y + z = 1 nên 0 ≤ x, y, z ≤ 1
Chứng minh \({\sqrt{2x^{2}+x+1}}\leq x+1.\)
⇔ \(\left({\sqrt{2x^{2}+x+1}}\right)^{2}\leq(x+1)^{2}\)
⇔ \(2x^{2}+x+1\leq x^{2}+2x+1\)
⇔ \(2x^{2}+x+1-x^{2}-2x-1\leq0\)
⇔ \(x^{2}-x\leq0\)
⇔ \(x\left(x-1\right)\leq0\)
Ta có: luôn đúng với 0 ≤ x ≤ 1
Chứng minh tương tự ta có:
\(\left\{\begin{array}{l}{{\sqrt{2y^{2}+y+1}\leq y+1}}\\ {{\sqrt{2z^{2}+z+1}\leq x+1}}\end{array}\right.\)
\(Q={\sqrt{2x^{2}+x+1}}+{\sqrt{2y^{2}+y+1}}\) + \({\sqrt{2z^{2}+z+1}}\)
≤ \((x+1)+(y+1)+(z+1)=(x+y+z)+3\)
Mà x + y + z = 1 nên Q ≤ 4
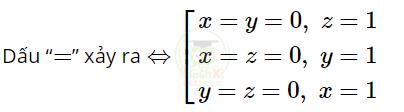
Vậy Q đạt giá trị lớn nhất bằng 4 khi x, y, z ∈ \(\{(0;\ 0;\ 1)\,,\ (0;\ 1;\ 0)\,,\ (1;\ 0;\ 0)\}.\)
Trên đây MATHX đã hướng dẫn các em giải đề thi giữa kì 2 môn toán lớp 9 năm học 2023 - 2024 - đề 1. Ngoài ra các bậc phụ huynh cần cho con em mình học đúng phương pháp và tham khảo các khóa học online tại MATHX.VN để giúp con tự tin chinh phục môn toán nhé.