
Thầy/cô MATHX biên soạn đề cương giữa kì 2 môn toán lớp 9 năm học 2023-2024 kèm đề tham khảo và bài tập tự luyện nhằm mục đích giúp các em học sinh ôn luyện kiến thức nhằm đạt kết quả tốt nhất cho kì thi giữa kì sắp tới. Chúc các em ôn tập tốt!
1. Dạng tổng quát:
\(\left\{ \begin{matrix} ax+by=c \\ {a}'x+{b}'y={c}' \\ \end{matrix}\text{ }\!\!~\!\!\text{ }\left( I \right) \right.\)
2. Số nghiệm:
+ Nếu \(\dfrac{a}{{{a}'}}\ne \dfrac{b}{{{b}'}}\) thì hệ phương trình (I) có duy nhất một nghiệm.
+ Nếu \(\dfrac{a}{{{a}'}}=\dfrac{b}{{{b}'}}=\dfrac{c}{{{c}'}}\) thì hệ phương trình (I) vô số nghiệm.
+ Nếu \(\dfrac{a}{{{a}'}}=\dfrac{b}{{{b}'}}\ne \dfrac{c}{{{c}'}}\) thì hệ phương trình (I) vô nghiệm.
3. Phương pháp giải
Ví dụ: Giải hệ phương trình
\(\left\{ \begin{array}{*{35}{l}} x+5y=7 \\ 3x-2y=4 \\ \end{array} \right.\)
- Phương pháp cộng đại số
\(\left\{ \begin{array}{*{35}{l}} x+5y=7 \\ 3x-2y=4 \\ \end{array}\Leftrightarrow \left\{ \begin{array}{*{35}{l}} 2x+10y=14 \\ 15x-10y=20 \\ \end{array} \right. \right.\)
\(\Leftrightarrow \left\{ \begin{array}{*{35}{l}} 17x=34 \\ 3x-2y=4 \\ \end{array}\Leftrightarrow \left\{ \begin{array}{*{35}{l}} x=2 \\ y=1 \\ \end{array} \right. \right.\)
- Phương pháp thế
\(\left\{ \begin{array}{*{35}{l}} x+5y=7 \\ 3x-2y=4 \\ \end{array}\Leftrightarrow \left\{ \begin{array}{*{35}{l}} x=7-5y \\ 3\left( 7-5y \right)-2y=4 \\ \end{array} \right. \right.\)
\(\Leftrightarrow \left\{ \begin{array}{*{35}{l}} x=2 \\ y=1 \\ \end{array} \right.\)
\(a{{x}^{2}}+bx+c=0\left( a\ne 0 \right)\)
Cách giải:
Tính \(\Delta\!\!\text{ }={{\mathbf{b}}^{2}}-4\mathbf{ac}\)
· Nếu \(\text{ }\!\!\Delta\!\!\text{ }<0\) thì phương trình vô nghiệm
· Nếu \(\text{ }\!\!\Delta\!\!\text{ }=0\) thì phương trình có nghiệm kép
\({{x}_{1}}={{x}_{2}}=\dfrac{-b}{2a}\)
· Nếu \(\text{ }\!\!\Delta\!\!\text{ }>0\) thì phương trình có 2 nghiệm phân biệt:
\({{x}_{1}}=\dfrac{-b+\sqrt{\text{ }\!\!\Delta\!\!\text{ }}}{2a};\text{ }\!\!~\!\!\text{ }{{x}_{2}}=\dfrac{-b-\sqrt{\text{ }\!\!\Delta\!\!\text{ }}}{2a}\)
1. Tính chất của hàm số \(y=a{{x}^{2}}\left( a\ne 0 \right)\)
· Nếu \(\text{a}>0\) thì hàm số đồng biến khi\( \text{x}>0\) , nghịch biến khi \(\text{x}<0\) và bằng 0 khi \(\text{x}=0\)
· Nếu \(\text{a}<0\) thì hàm số đồng biến khi \(\text{x}<0\), nghịch biến khi \(\text{x}>0\) và bằng 0 khi \(\text{x}=0\)
2. Đồ thị hàm số \(\mathbf{y}=\mathbf{a}{{\mathbf{x}}^{2}}\left( \text{a}\ne 0 \right)\) là một parabol có đỉnh là điểm \(\text{O}\left( 0;0 \right)\), nhận \(\text{Oy}\) là trục đối xứng.
· Nếu \(\text{a}>0\) thì đồ thị nằm phía trên trục hoành và nhận điểm \(\text{O}\left( 0;0 \right)\) là điểm thấp nhất.
· Nếu \(\text{a}<0\) thì đồ thị nằm phía dưới trục hoành và nhận điểm \(\text{O}\left( 0;0 \right)\) là điểm cao nhất.

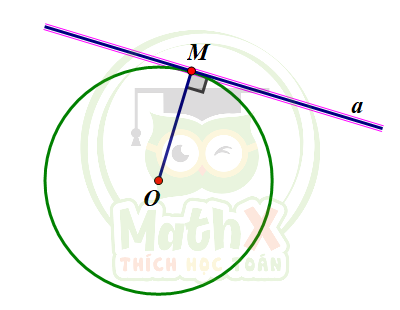
\(A \perp OM\) tại \(M\) và \(M \in (O)\)
=> \(a\) là tiếp tuyến của \((O)\)
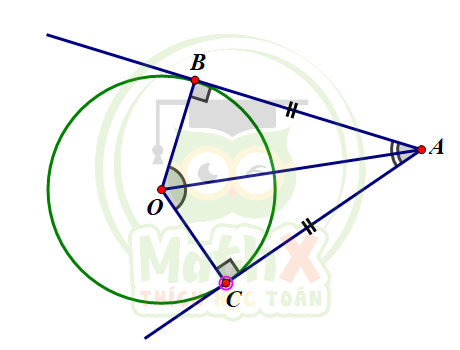
- \(AB, AC\) là hai tiếp tuyến của đường tròn \((O)\)
=>
\(AB = AC\)
\(AO\) là tia phân giác của \(\widehat {BAC}\)
\(OA\) là tia phân giác của \(\widehat {BOC}\)
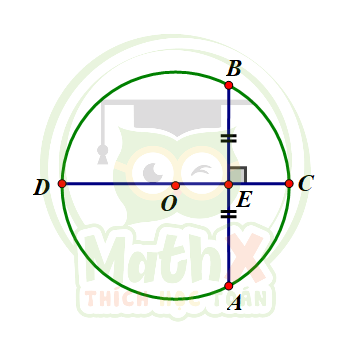
- Đường kính \(CD\) vuông góc với dây \(AB\) tại \(E\)
=>
\(E\) là trung điểm của \(AB\)
\(C, D\) là điểm chính giữa của cung \(AB\)
- Đường kính \(CD\) đi qua trung điểm \(E\) của dây \(AB\) (không đi qua tâm \(O\))
=>
\(CD \perp AB\) tại E
\(C, D\) là điểm chính giữa của cung \(AB\)
- Đường kính \(CD\) đi qua điểm chính giữa \(C\) của cung \(AB\)
=>
\(CD \perp AB\) tại E
\(E\) là trung điểm của \(AB\)
Trong một đường tròn:
- Hai dây bằng nhau căng hai cung bằng nhau và ngược lại
- Dây lớn hơn căng cung lớn hơn và ngược lại
- Hai cung bị chắn giữa hai dây song song thì bằng nhau
- Góc ở tâm bằng số đo cung bị chắn
- Góc nội tiếp bằng nửa số đo của cung bị chắn
- Góc nội tiếp chắn nửa đường tròn là góc vuông
- Các góc nội tiếp cùng chắn một cung (chắn các cung bằng nhau trong một đường tròn) thì bằng nhau
- Các góc nội tiếp bằng nhau thì chắn các cung bằng nhau
- Góc nội tiếp chắn cung có số đo \(\leq 90^o\) thì bằng nửa số đo của góc ở tâm chắn cung đó
- Góc tạo bởi tia tiếp tuyến với dây cung bằng nửa số đo của cung bị chắn
- Góc tạo bởi tia tiếp tuyến với dây cung và góc nội tiếp cùng chắn một cung (chắn hai cung bằng nhau trong một đường tròn) thì bằng nhau
- Góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo của hai cung bị chắn
- Góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo của hai cung bị chắn
- Tâm của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác, bán kính là khoảng cách từ tâm đến mỗi đỉnh tam giác
- Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền
- Tâm của đường tròn nội tiếp tam giác là giao điểm của ba đường phân giác của tam giác, bán kính là khoảng cách từ tâm đến mỗi cạnh tam giác
- Tứ giác có 4 đỉnh cách đều một điểm (4 đỉnh nằm trên một đường tròn)
- Tứ giác có tổng hai góc đối bằng \(180^o\)
- Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới một góc không đổi
- Tứ giác có góc ngoài tại một đỉnh bằng với góc trong có đỉnh đối diện
- Hình chữ nhật, hình vuông, hình thang cân nội tiếp đường tròn
- Tổng 2 góc bằng \(180^o\)
- Hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới một góc không đổi
- Góc ngoài tại một đỉnh bằng với góc trong có đỉnh đối diện
- Hình thang nội tiếp đường tròn là hình thang cân
I. TRẮC NGHIỆM (3 ĐIỂM)
Câu 1. Phương trình nào dưới đây là phương trình bậc nhất hai ẩn?
A. \(2x-y=3\) B. \(2x+3=0\) C. \({{x}^{2}}+4x+3=0\)
Câu 2. Với $x>0$ thì hàm số nào dưới đây đồng biến?
A. \(y=-2{{x}^{2}}\) B. \(y=-{{x}^{2}}\) C. \(y={{x}^{2}}\)
Câu 3. Đồ thị của hàm số \(y=a{{x}^{2}}\left( a\ne 0 \right)\) là một
A. đường thẳng B. đường gấp khúc C. đường cong
Câu 4. Cho hình vẽ, góc nội tiếp là
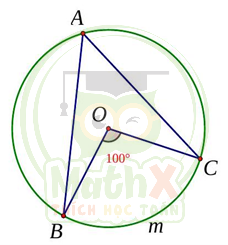
A. \(\widehat{BAC}\) B. \(\widehat{BOC}\) C. \(\widehat{ACO}\)
Câu 5. Tứ giác nội tiếp đường tròn là tứ giác có
A. bốn đỉnh nằm bên trong đường tròn
B. ba đỉnh nằm trên đường tròn
C. bốn đỉnh nằm trên đường tròn
Câu 6. Trong một đường tròn,
A. hai dây bằng nhau căng hai cung không bằng nhau
B. dây nào lớn hơn căng cung nhỏ hơn.
C. cung nào lớn hơn căng dây lớn hơn.
II. TỰ LUẬN (7 ĐIỂM)
Câu 7 (1,5 điểm): Hãy cho biết số nghiệm của các hệ phương trình sau:
\(\left\{ \begin{array}{*{35}{l}} x-3y=-1 \\ 2x-6y=5 \\ \end{array};\text{ }\!\!~\!\!\text{ }\left\{ \begin{matrix} 1,2x-2y=0,4 \\ -3x+5y=1 \\ \end{matrix} \right. \right.\)
Câu 8 (1,5 điểm):
a) Giải hệ phương trình
\(\left\{ \begin{array}{*{35}{l}} 3x+2y=1 \\ 5x+3y=2 \\ \end{array} \right.\)
b) Giải phương trình
\({{x}^{2}}+3x-28=0\)
Câu 9 (1 điểm):
Vẽ đồ thị hàm số \(\left( P \right):y=\dfrac{3}{4}{{x}^{2}}\)
Câu 10 (1 điểm):
Hai xe cùng khởi hành một lúc ở hai tỉnh \(A\) và \(B\) cách nhau \(60\text{ }\!\!~\!\!\text{ km}\). Nếu đi ngược chiều thì gặp nhau sau 1 giờ; nếu đi cùng chiều thì xe đi nhanh hơn sẽ đuổi kịp xe kia sau 3 giờ. Tìm vận tốc mỗi xe.
Câu 11 (2 điểm):
Từ điểm \(C\) ở ngoài đường tròn \(\left( \text{O} \right)\), vẽ \(\text{CA}\) và \(\text{CB}\) là các tiếp tuyến của đường tròn (O) ( \(\text{A},\text{B}\) là các tiếp điểm).
a) Chứng minh tứ giác \(\text{CAOB}\) nội tiếp được đường tròn.
b) Qua \(\text{B}\) vẽ đường thẳng song song với \(\text{CA}\), cắt đường tròn \(\left( \text{O} \right)\) tại điểm \(\text{D}\left( D\ne B \right)\). \(\text{CD}\) cắt đường tròn \(\left( \text{O} \right)\) tại điểm \(\text{E}\left( E\ne D \right)\). Chứng minh \({{CB}^{2}}=CE. CD\).
c) Tia \(BE\) cắt \(\text{CA}\) tại \(\text{F}\). Chứng minh \(\text{F}\) là trung điểm của \(CA\).
HẾT
Bài 1. Phương trình nào dưới đây là phương trình bậc nhất hai ẩn?
\(3x-y=2; \\ 3{{x}^{2}}+4y=5; \\ \text{ }\!\!~\!\!\text{ }5x-y+z=0\)
Bài 2. Dự đoán số nghiệm của các hệ phương trình sau:
a) \(\left\{ \begin{matrix} x+y=2 \\ -2x+y=-1 \\ \end{matrix} \right.\)
b) \(\left\{ \begin{matrix} 3x-y=1 \\ 27x-9y=3 \\ \end{matrix} \right.\)
c) \(\left\{ \begin{matrix} x-0,5y=2 \\ 2x-y=4 \\ \end{matrix} \right.\)
Bài 3.Với \(x>0\) thì hàm số nào sau đây là hàm số đồng biến
\(y={{x}^{2}}; \\ \text{ }\!\!~\!\!\text{ }y=-3{{x}^{2}}; \\ \text{ }\!\!~\!\!\text{ }y=\dfrac{1}{2}{{x}^{2}}\)
Bài 4. Với \(x>0\) thì hàm số nào sau đây là hàm số nghịch biến
\(y={{x}^{2}}; \\ y=-3{{x}^{2}}; \\ y=0,5{{x}^{2}}\)
Bài 5.
a) Vẽ \(\left( P \right):y=\dfrac{1}{2}{{x}^{2}}\) b) Vẽ \(\left( P \right):y=-1,5{{x}^{2}}\)
Bài 6. Giải các phương trình sau:
a) \(6{{x}^{2}}-7x+1=0\). b) \({{x}^{2}}+4x-5=0\)
Bài 7. Giải các hệ phương trình sau:
a) \(\left\{ \begin{matrix} 2x-y=5 \\ x+y=4 \\ \end{matrix} \right.\)
b) \(\left\{ \begin{array}{*{35}{l}} 2x+y=5 \\ x+7y=9 \\ \end{array} \right.\)
Bài 8. Hai bạn An và Vy đi xe đạp cùng lúc ngược chiều nhau, cách nhau \(4\text{ }\!\!~\!\!\text{ km}\) đến trường. Sau \(12\) phút hai bạn gặp nhau ở trường. Tính vận tốc đi xe đạp của mỗi bạn biết vận tốc đi xe đạp của An hơn Vy là \(2\text{ }\!\!~\!\!\text{ km}/\text{h}\).
Bài 9. Hai đội xe chở cát để san lấp một khu đất. Nếu hai đội cùng làm thì trong \(18\) ngày xong công việc. Nếu đội 1 làm \(6\) ngày, sau đó đội thứ 2 làm tiếp \(8\) ngày nữa thì được \(40\text{ }\!\!\%\!\!\text{ }\) công việc. Hỏi mỗi đội làm một mình thì bao lâu xong công việc.
Bài 10. Một khu vườn hình chữ nhật có chu vi \(46\) mét, nếu tăng chiều dài \(5\text{ }\!\!~\!\!\text{ m}\) và giảm chiều rộng \(3\text{ }\!\!~\!\!\text{ m}\) thì chiều dài gấp \(4\) lần chiều rộng. Tính diện tích khu vườn.
Bài 11. Nhân dịp 26/03, một trường THCS tổ chức cho \(190\) người bao gồm giáo viên và học sinh khối 9 đi tham quan khu du lịch Hồ Mây. Biết giá vé vào cổng của một giáo viên là \(400000\) đồng, vé vào cổng của một học sinh là \(300000\) đồng. Nhưng vì là người địa phương nên được giảm \(20\text{ }\!\!\%\!\!\text{ }\) cho mỗi vé vào cổng, vì vậy, nhà trường chỉ phải trả tổng số tiền là \(46960000\) đồng. Hỏi có bao nhiêu giáo viên và học sinh khối 9 của trường đi tham quan?
Bài 12. Cho hình vẽ.
a) Hãy cho biết số đo của các cung nhỏ \(\text{AC}\) và \(\text{BD}\).
b) Tính \(\widehat{BED}\).
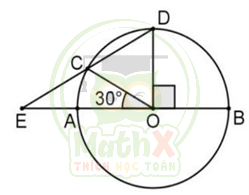
Bài 13. Cho hình vẽ, biết số đo cung nhỏ \(\text{BC} = {{40}^{\circ }}\) và số đo cung nhỏ \(\text{AD} = {{130}^{\circ }}\). Tính \(\widehat{ABD};\widehat{AFD};\widehat{AED}\).
Bài 14. Cho nửa đường tròn tâm \(\text{O}\), đường kính \(\text{AB}\). \(\text{C}\) là điểm chính giữa của nửa đường tròn. Gọi \(\text{E}\) là trung điểm của \(\text{BC}\). Vẽ \(\text{EH}\) vuông góc với \(\text{AB}\) tại \(\text{H}\).
a) Chứng minh tứ giác \(\text{ACEH}\) nội tiếp đường tròn.
b) Tính \(\widehat{HEB}\).
c) Tia \(\text{AE}\) cắt nửa đường tròn \(\text{(O)}\) tại \(\text{F}\). Chứng minh \(\text{EA}. \text{EF}=\text{EB}.\text{EC}\)
d) Vẽ CG vuông góc \(AF\) tại \(G\). Chứng minh \(OG\) là tia phân giác \(\widehat {COF}\).
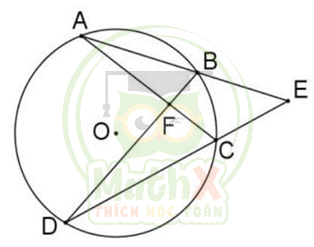
Bài 15. Từ điểm \(A\) nằm ngoài đường tròn \(\left( O \right)\), vẽ hai tiếp tuyến \(AB,AC\) (\(B,C\) là các tiếp điểm).
a) Chứng minh tứ giác \(ABOC\) nội tiếp.
b) Vẽ dây \(CD\) song song với \(AB\). Chứng minh \(\widehat{BCD}=\widehat{BDC}\).
c) Vẽ \(CF\bot AB\) tại \(F\), tia \(BO\) cắt \(CD\) ở \(E\). Chứng minh \(CF.CO=CA. CE\)
Bài 16. Từ điểm \(\text{D}\) nằm ngoài đường tròn \(\left( \text{O} \right)\), vẽ hai tiếp tuyến \(\text{DB}\) và \(\text{DC}\) (\(\text{B},\text{C}\) là các tiếp điểm). Vẽ \(\text{CF}\bot \text{BD}\) tại \(\text{F}\),\(\text{CF}\) cắt cung nhỏ \(\text{BC}\) ở \(\text{G}\).
a) Chứng minh tứ giác \(\text{OBDC}\) nội tiếp.
b) Chứng minh \(\widehat{FBG}=\widehat{FCB}\) và \({{FB}^{2}}=FG.FC\)
c) Vẽ dây \(\text{BA}//\text{CD}\), tia \(\text{CO}\) cắt \(\text{AB}\) ở E. Chứng minh tứ giác \(BECF\) nội tiếp và \(\text{EF}//\text{AG}\).
d) Chứng minh \(\widehat{BCG}=\widehat{BCE}=\widehat{ACE}\).
Các em xem thêm một số bài viết về chủ đề toán lớp 9 tại đây:
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 1
GIẢI CÂU HỎI CUỐI TRONG ĐỀ THI HỌC KÌ 1 TOÁN 9 QUẬN HAI BÀ TRƯNG 2023 2024 - MATHX
Một bài toán hay về phương trình vô tỉ và cách giải - đề khảo sát THCS Dịch Vọng Hậu
Trên đây là đề cương ôn tập giữa học kì 2 toán lớp 9 năm học 2023 - 2024 và một số bài tập tự luyện cùng đề thi thử tham khảo. Đây hoàn toàn là các bài tập ở cấp độ cơ bản nên các thầy/cô sẽ không làm giải nữa. Các em học sinh chủ động làm bài, nếu có thắc mắc có thể nhắn tin đến Fanpage của Mathx trên Facebook để được các thầy/cô giải đáp tận tình nhé
Ngoài ra các quý phụ huynh và các em học sinh có thể tham khảo các khóa học online tại MATHX.VN để giúp con cải thiện môn toán.