MỘT SỐ CÂU HỎI HÌNH HỌC TRONG ĐỀ THI CUỐI KÌ I LỚP 8 CỦA CÁC TRƯỜNG (BỘ SÁCH: CÁNH DIỀU)

MATHX gửi quý phụ huynh và các em học sinh một số câu hỏI hình học trong đề thi cuối kì I lớp 8 của các trường (bộ sách cánh diều) kèm đáp án chi tiết.

Câu 1. (Trường THCS Hiệp Phú – TP. Hồ Chí Minh, năm 2024 – 2025)

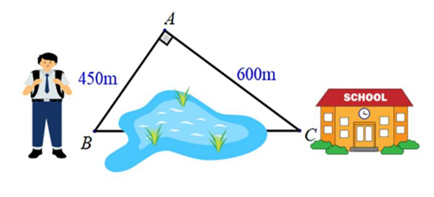
Nhà bạn Nam tại vị trí điểm B. Hằng ngày, Nam đi học theo con đường từ B đến A và từ A đến trường tại vị trí điểm C như hình vẽ do khoảng giữa BC là một con sông lớn. Hiện nay, chính quyền địa phương đã làm cầu nên Nam đi học theo con đường thẳng BC. Biết đoạn đường BA là 450 m, đoạn đường AC là 600 m và BA vuông góc với AC.

a) Tính quãng đường BC bạn Nam đi học.

b) Hỏi khi Nam đi theo đường thẳng BC để đến trường thì gần hơn so với đi đường cũ bao nhiêu mét?

Hướng dẫn:

a) Xét ΔABC có \( \widehat{BAC} = 90^\circ \) ⇒ \( AB^2 + AC^2 = BC^2 \) (Định lý Pythagore)

⇒ \( BC = \sqrt{AB^2 + AC^2} = \sqrt{450^2 + 600^2} = 750 \text{ (m)} \)

Vậy quãng đường BC bạn Nam đi học dài 750 m.

b) Quãng đường cũ mà bạn Nam đi học là: \( AB + AC = 450 + 600 = 1050 \text{ (m)} \)

Quãng đường BC gần hơn quãng đường cũ số mét là: \( 1050 - 750 = 300 \text{ (m)} \)

Vậy khi Nam đi theo đường thẳng BC để đến trường thì gần hơn so với đi đường cũ 300 mét.

---

Câu 2. (Trường THCS Lê Văn Tám – TP.HCM, năm 2024 – 2025)

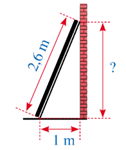
Một thanh gỗ dài 2,6 m dựa vào một bức tường thẳng đứng (như hình vẽ). Chân của thanh gỗ cách mép tường một khoảng là 1 m. Tính khoảng cách từ điểm thanh gỗ chạm vào tường đến mặt đất là bao nhiêu mét?

Hướng dẫn:

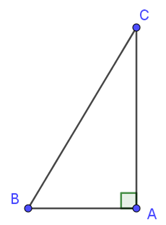
Gọi đầu thanh gỗ chạm vào bờ tường là điểm C, chân thanh gỗ chạm xuống đất là điểm B, góc tường là điểm A.

Xét ΔABC có \( \widehat{BAC} = 90^\circ \) ⇒ \( AB^2 + AC^2 = BC^2 \) (Định lý Pythagore)

⇒ \( AC^2 = BC^2 - AB^2 = 2,6^2 - 1^2 = 5,76 \text{ (m\(^2\)) } \)

⇒ \( AC = 2,4 \text{ (m)} \)

Vậy khoảng cách từ điểm thanh gỗ chạm vào tường đến mặt đất là 2,4 mét.

---

Câu 3. (Trường THCS Thanh Nê – Thái Bình, năm 2024 – 2025)

Một khối Rubik có dạng hình chóp tam giác đều. Biết chiều cao bằng 5,2 cm, thể tích của khối Rubik là 45,24 cm³. Tính diện tích đáy của khối Rubik.

Hướng dẫn:

Gọi V, S, h lần lượt là thể tích, diện tích mặt đáy, chiều cao của khối Rubik.

\( V = \dfrac{1}{3}Sh \) ⇒ \( S = \dfrac{3V}{h} = \dfrac{3 \cdot 45,24}{5,2} = 26,1 \text{ (cm}^2\text{)} \)

Vậy diện tích đáy của khối Rubik là 26,1 cm².

---

Câu 4. (Trường THCS Phước Lộc – Bình Định, năm 2024 – 2025)

Mái nhà của một chòi trên bãi biển có dạng hình chóp tứ giác đều như hình bên. Tính diện tích vải bạt cần dùng để phủ mái chòi, biết rằng người ta chỉ dùng một lớp vải bạt (không tính phần hiên xung quanh).

Hướng dẫn:

Gọi đỉnh của hình chóp là S, bốn góc của mái chòi là A, B, C, D.

Mái chòi là hình chóp \( S.ABCD \).

Gọi \( SH \) là đường cao của tam giác \( SAB \).

Khi đó \( SH \) là trung đoạn của hình chóp \( S.ABCD \).

Có \( \triangle SAB \) cân tại \( S \) ⇒ \( SA = SB = 1,2 \text{ (m)} \).

Vì \( \triangle SAB \) cân tại \( S \) ⇒ \( SH \) là đường cao, đồng thời là đường trung tuyến

⇒ \( AH = BH = \dfrac{1}{2}AB = \dfrac{1}{2} \cdot 1,5 = 0,75 \text{ (m)} \).

Xét \( \triangle SHB \) vuông tại \( H \) có:

⇒ \( SH = \sqrt{SB^2 - BH^2} = \sqrt{1,2^2 - 0,75^2} \approx 0,94 \text{ (m)} \)

Diện tích vải bạt cần dùng để phủ mái chòi chính là diện tích xung quanh của hình chóp tứ giác đều đó.

Diện tích xung quanh của hình chóp là:

⇒ \( S_{xq} = \dfrac{4 \cdot 1,5}{2} \cdot 0,94 = 2,82 \text{ (m}^2\text{)} \)

Vậy diện tích vải bạt cần dùng để phủ mái chòi là 2,82 m².

---

Câu 5. (Trường THCS Trường Chinh – Hồ Chí Minh, năm 2024 – 2025)

Một hộp quà lưu niệm có dạng hình chóp tứ giác đều \( S.ABCD \), biết cạnh CD = 36 cm, đường cao SO = 24 cm, trung đoạn SH = 30 cm.

a) Tính diện tích xung quanh hộp quà hình chóp tứ giác đều \( S.ABCD \).

b) Chuẩn bị trang trí cho cây thông NOEL, bạn Mai làm 10 hộp quà gắn lên cây thông. Mỗi hộp quà, Mai đều dán giấy màu lên toàn bộ các mặt (cả mặt bên và mặt đáy), biết diện tích giấy hao hụt khi làm là 10%. Hỏi Mai phải chuẩn bị diện tích giấy dán bằng bao nhiêu để làm 10 hộp quà như hình dạng trên.

Hướng dẫn:

a) Nửa chu vi đáy của hộp quà là:

\( \frac{36 \cdot 4}{2} = 72\text{ cm} \)

Diện tích xung quanh của hộp quà hình chóp tứ giác đều \( S.ABCD \) là:

\( S_{xq} = 72 \cdot 30 = 2160\text{ cm}^2 \)

b) Diện tích toàn phần của hộp quà là:

\( S_{tp} = 2160 + 36^2 = 3456\text{ cm}^2 \)

Diện tích toàn phần của 10 hộp quà là: \( 34560\text{ cm}^2 \)

Vì diện tích giấy hao hụt khi làm là 10% nên bạn Mai đã dùng 90% lượng giấy đã chuẩn bị để dán hết các mặt của 10 hộp quà.

Diện tích giấy Mai cần chuẩn bị là: \( \frac{34560}{0.9} = 38400\text{ cm}^2 \)

---

Câu 6. (Trường THCS Hoa Lư – Hồ Chí Minh, năm 2024 – 2025)

Cho ΔDEF vuông tại E (EF < ED) và H là trung điểm của DF.
Kẻ HI ⟂ ED (I ∈ ED), HK ⟂ EF (K ∈ EF).

a) Chứng minh tứ giác EIHK là hình chữ nhật.

b) Chứng minh tứ giác FKHI là hình bình hành.

c) Kẻ đường cao EB của tam giác DEF. Chứng minh BK ⟂ BI.

Hướng dẫn:

a) Có \( HK \perp BE \); \( HI \perp EC \) ⇒ \( \widehat{HKE} = \widehat{HIE} = 90^\circ \).

Xét tứ giác \( EIHK \) có \( \widehat{HKE} = \widehat{KEI} = \widehat{EIH} = 90^\circ \)

⇒ Tứ giác \( EIHK \) là hình chữ nhật (dấu hiệu nhận biết).

b) Xét \( \triangle FED \) vuông tại \( E \) có \( EH \) là trung tuyến (Do \( HF = HD = \dfrac{1}{2}FD \))

⇒ \( HE = HF \) (tính chất đường trung tuyến trong tam giác vuông).

Xét \( \triangle EFH \) có \( HF = HE \) ⇒ \( \triangle EFH \) cân tại \( H \) mà \( HK \) là đường cao

⇒ \( HK \) là đường trung tuyến của tam giác.

⇒ \( FK = KE \) mà \( IH = KE \) (do \( EKHI \) là hình chữ nhật).

⇒ \( FK = IH (= KE) \).

Xét tứ giác \( FKIH \) có \( FK = HI \), \( FK \parallel HI \) (do \( EKHI \) là hình chữ nhật)

⇒ Tứ giác \( FKIH \) là hình bình hành (dấu hiệu nhận biết).

c) Gọi \( A \) là giao của \( KI \) và \( EH \).

Có \( EKHI \) là hình chữ nhật ⇒ \( AH = AI = AE = AK \).

Xét \( \triangle BHE \) có \( \widehat{EBH} = 90^\circ \); \( BA \) là đường trung tuyến

⇒ \( AB = AE = AH \) (tính chất đường trung tuyến trong tam giác vuông).

Mà \( AH = AI = AE = AK \) ⇒ \( AK = AB = AI = \dfrac{1}{2}KI \).

Xét \( \triangle KBI \) có \( BA \) là đường trung tuyến, \( BA = \dfrac{1}{2}KI \)

⇒ \( \triangle KBI \) vuông tại \( B \) hay \( BI \perp BK \).

---

Câu 7. (Trường THCS Ninh Nhất – Ninh Bình, năm 2024 – 2025)

Cho tam giác \( ABC \), đường cao \( AH \). Gọi \( I \) là trung điểm của \( AC \). Trên tia đối của tia \( IH \) lấy điểm \( D \) sao cho \( I \) là trung điểm của \( HD \).

a) Chứng minh tứ giác \( AHCD \) là hình chữ nhật.

b) Từ \( H \) vẽ tia \( Hx \) song song với \( AC \) và cắt tia \( DC \) tại \( M \). Kẻ \( IK \) vuông góc với \( HC \) (\( K \in HC \)). Chứng minh ba điểm \( A, K, M \) thẳng hàng.

Hướng dẫn:

a) Xét tứ giác \( ADCH \) có \( I \) là trung điểm của \( AC \), \( I \) là trung điểm của \( HD \)

⇒ \( ADCH \) là hình bình hành (dấu hiệu nhận biết).

Mà \( \widehat{AHC} = 90^\circ \) (vì \( AH \perp BC \))

⇒ \( AHCD \) là hình chữ nhật (dấu hiệu nhận biết).

b) Có \( AHCD \) là hình chữ nhật, \( AC \cap DH = I \)

⇒ \( HI = CI \), \( AH \parallel CD \) (tính chất hình chữ nhật).

Xét \( \triangle HIC \) có \( HI = IC \)

⇒ \( \triangle HIC \) cân tại \( I \) (dấu hiệu nhận biết).

Mà \( IK \) là đường cao của \( \triangle HIC \) (do \( IK \perp HC \))

⇒ \( IK \) là đường trung tuyến hay \( K \) là trung điểm của \( HC \).

Xét tứ giác \( AHCN \) có \( AC \parallel HM \), \( AH \parallel CM \)

⇒ \( AHCN \) là hình bình hành (dấu hiệu nhận biết).

⇒ \( HC \) và \( AM \) cắt nhau tại trung điểm của mỗi đoạn.

Mà \( K \) là trung điểm của \( HC \)

⇒ \( K \) cũng là trung điểm của \( AM \)

⇒ \( A, K, M \) thẳng hàng.

---

Câu 8. (Trường THCS Nguyễn Bỉnh Khiêm – Hà Nội, năm 2024 – 2025)

 

Cho \( \triangle ABC \) vuông tại \( A \), đường cao \( AH \). Từ \( H \) kẻ \( HM \) vuông góc \( AB \) tại \( M \) và \( HN \) vuông góc \( AC \) tại \( N \).

a) Chứng minh \( AMHN \) là hình chữ nhật.

b) Trên tia đối của tia \( MH \), lấy điểm \( D \) sao cho \( MH = MD \). Trên tia đối của tia \( NH \), lấy điểm \( E \) sao cho \( NH = NE \). Chứng minh tứ giác \( AMNE \) là hình bình hành.

c) Chứng minh \( A \) là trung điểm của \( DE \).

Hướng dẫn:

a) Có \( MH \perp AB \), \( HN \perp AC \) ⇒ \( \widehat{HMA} = \widehat{HNA} = 90^\circ \).

Xét tứ giác \( HMAN \) có \( \widehat{HMA} = \widehat{MAN} = \widehat{ANH} = 90^\circ \)

⇒ Tứ giác \( HMAN \) là hình chữ nhật (dấu hiệu nhận biết).

b) Có \( HMAN \) là hình chữ nhật

⇒ \( AM \parallel HN \), \( AM = HN \), \( MH = AN \) (tính chất hình chữ nhật).

Mà \( HN = NE \) ⇒ \( NE = AM (= HN) \).

Xét tứ giác \( AMNE \) có \( AM \parallel NE \), \( AM = NE \)

⇒ Tứ giác \( AMNE \) là hình bình hành (dấu hiệu nhận biết).

c) Có \( AMNE \) là hình bình hành

⇒ \( MN \parallel AE \), \( ME = AE \) (tính chất hình bình hành).

Có \( MH = AN \), \( MH = MD \) ⇒ \( DM = AN (= MH) \).

Xét tứ giác \( DMAN \) có \( DM \parallel AN \), \( DM = AN \)

⇒ \( DMAN \) là hình bình hành ⇒ \( MN \parallel DA \), \( MN = DA \).

Qua \( A \), có \( AD \parallel MN \), \( AE \parallel MN \) ⇒ \( D, A, E \) thẳng hàng (1).

Có \( AD = MN \), \( AE = MN \) ⇒ \( AD = AE (= MN) \) (2).

Từ (1) và (2) ⇒ \( A \) là trung điểm của \( DE \).

---

Câu 9. (Trường THCS Lương Thế Vinh – Nam Định, năm 2024 – 2025)

Cho \( \triangle ABC \) vuông tại \( A \) (\( AB < AC \)), \( E \) là trung điểm của \( BC \). Kẻ \( EF \) vuông góc với \( AB \) tại \( F \), \( ED \) vuông góc với \( AC \) tại \( D \).

a) Chứng minh \( AE = DF \).

b) Lấy điểm \( K \) sao cho \( D \) là trung điểm của \( EK \). Chứng minh tứ giác \( AECK \) là hình thoi.

c) Kẻ \( EM \) vuông góc với \( AK \) tại \( M \). Chứng minh \( \widehat{DMF} = 90^\circ \).

Hướng dẫn:

a) Có \( EF \perp AB \); \( ED \perp AC \) ⇒ \( \widehat{EFA} = \widehat{EDA} = 90^\circ \).

Xét tứ giác \( AFED \) có \( \widehat{FAD} = \widehat{EFA} = \widehat{EDA} = 90^\circ \)

⇒ \( AFED \) là hình chữ nhật (dấu hiệu nhận biết) ⇒ \( AE = DF \) (tính chất hình chữ nhật).

b) Xét \( \triangle ABC \) có \( \widehat{BAC} = 90^\circ \), \( AE \) là trung tuyến của \( \triangle ABC \)

⇒ \( EA = EB = EC \) (tính chất đường trung tuyến trong tam giác vuông).

Xét \( \triangle AEC \) có \( EA = EC \) ⇒ \( \triangle EAC \) cân tại \( E \).

Mà \( ED \) là đường cao của \( \triangle AEC \) (do \( ED \perp AC \))

⇒ \( ED \) là đường trung tuyến hay \( D \) là trung điểm của \( AC \).

Xét tứ giác \( AECK \) có \( D \) là trung điểm của \( AC \), đồng thời \( D \) cũng là trung điểm của \( EK \)

⇒ \( AECK \) là hình bình hành (dấu hiệu nhận biết), mà \( EK \perp AC \)

⇒ \( AECK \) là hình thoi (dấu hiệu nhận biết).

c) Gọi \( I \) là giao điểm của \( AE \) và \( DF \).

Khi đó \( IF = IE = ID = IA \) (do \( AFED \) là hình chữ nhật).

Xét \( \triangle AME \) vuông tại \( M \) có \( M I\) là đường trung tuyến

⇒ \( IA = IE = IM \) (tính chất đường trung tuyến trong tam giác vuông).

Mà \( IF = IE = ID = IA \) ⇒ \( IF = ID = IM = \dfrac{1}{2}FD \).

Xét \( \triangle FMD \) có \( MI \) là đường trung tuyến, \( MI = \dfrac{1}{2}FD \)

⇒ \( \triangle FMD \) vuông tại \( M \) hay \( \widehat{FMD} = 90^\circ \).

---

Câu 10. (Trường THCS Châu Đức – Bà Rịa Vũng Tàu, năm 2024 – 2025)

Cho tam giác \( \triangle ABC \) vuông tại \( A \) (\( AB > AC \)). Gọi \( M \) là trung điểm của \( BC \).

Trên tia \( AM \) lấy điểm \( D \) sao cho \( M \) là trung điểm của \( AD \).

a) Cho biết \( AB = 4 \, \text{cm} \), \( AC = 3 \, \text{cm} \). Tính độ dài đoạn thẳng \( BC \).

b) Chứng minh tứ giác \( ABDC \) là hình chữ nhật.

c) Gọi \( E \) là điểm đối xứng với \( C \) qua \( A \). Chứng minh tứ giác \( ADBE \) là hình bình hành.

d) Tia \( EM \) cắt \( AB \) tại \( K \) và cắt \( CD \) tại \( I \). Vẽ \( IH \perp AB \) (\( H \in AB \)). Chứng minh \( \triangle IKB \) cân.

Hướng dẫn:

a) Xét \( \triangle ABC \) có \( \widehat{BAC} = 90^\circ \) ⇒ \( AB^2 + AC^2 = BC^2 \) (định lý Pythagore).

⇒ \( BC = \sqrt{AB^2 + AC^2} = \sqrt{3^2 + 4^2} = 5 \) (cm).

b) Xét tứ giác \( ABDC \) có \( MB = MC = \dfrac12 BC \), \( MA = MD = \dfrac12 AD \), \( BC \cap AD = \{M\} \).

⇒ \( ABDC \) là hình bình hành (dấu hiệu nhận biết).

Mà \( \widehat{BAC} = 90^\circ \)⇒ \( ABDC \) là hình chữ nhật (dấu hiệu nhận biết).

c) Do \( ABDC \) là hình chữ nhật

⇒ \( MC = MB = \dfrac12 BC \), \( AC = BD \), \( \widehat{ACI} = 90^\circ \), \( AC \parallel BD \) (dấu hiệu nhận biết).

Có \( AC = AE \), \( AC = BD \) ⇒ \( AE = BD (= AC) \).

Xét tứ giác \( ADBE \) có \( AE \parallel BD \), \( AE = BD \)

⇒ \( ADBE \) là hình bình hành (dấu hiệu nhận biết).

d) Xét tứ giác \( ACIH \) có \( \widehat{ACI} = \widehat{CAH} = \widehat{AHI} = 90^\circ \) ⇒ \( ACIH \) là hình chữ nhật.

⇒ \( AC \parallel IH \), \( AC = IH \) mà \( AC = AE \) ⇒ \( IH = AE \).

Xét tứ giác \( AIHE \) có \( IH \parallel AE \), \( IH = AE \) ⇒ \( AIHE \) là hình bình hành.

⇒ \( AK = KH \) (tính chất hình bình hành).

Xét \( \triangle BCE \) có \( EM \) là đường trung tuyến (do \( MB = MC = \dfrac12 BC \)), \( BA \) là đường trung tuyến (do \( AC = AE = \dfrac12 EC \)), \( AB \cap EM = \{K\} \).

⇒ \( K \) là trọng tâm của \( \triangle BCE \) (định nghĩa).

⇒ \( \dfrac{BK}{BA} = \dfrac23 \) ⇒ \( \dfrac{AK}{BK} = \dfrac12 \) ⇒ \( \dfrac{KH}{BK} = \dfrac12 \).

⇒ \( H \) là trung điểm của \( KB \) hay \( IH \) là trung tuyến của \( \triangle KIB \).

Xét \( \triangle KIB \) có \( IH \) là đường cao, đồng thời là đường trung tuyến

⇒ \( \triangle KIB \) cân tại \( I \) (dấu hiệu nhận biết).

---