PHƯƠNG PHÁP CHỨNG MINH 3 ĐIỂM THẲNG HÀNG

MATHX gửi quý phụ huynh và các em học sinh phương pháp chứng minh 3 điểm thẳng hàng  lớp 7 của các trường kèm đáp án chi tiết.

CHỨNG MINH BA ĐIỂM THẲNG HÀNG

A. Kiến thức cần nhớ

Ba điểm cùng thuộc một đường thẳng gọi là ba điểm thẳng hàng. Để chứng minh ba điểm thẳng hàng, chúng ta có thể sử dụng một số phương pháp sau đây:

1. Phương pháp 1.
Nếu \( \widehat{ABD} + \widehat{DBC} = 180^\circ \) thì ba điểm A; B; C thẳng hàng.

2. Phương pháp 2.
Nếu AB // a và AC // a thì ba điểm A; B; C thẳng hàng.
(Cơ sở của phương pháp này là: tiên đề Ơ–Clit)

3. Phương pháp 3.
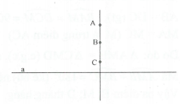
Nếu AB ⟂ a; AC ⟂ a thì ba điểm A; B; C thẳng hàng.
(Cơ sở của phương pháp này là: Có một và chỉ một đường thẳng a’ đi qua điểm O và vuông góc với đường thẳng a cho trước)
Hoặc A; B; C cùng thuộc một đường trung trực của một đoạn thẳng.

4. Phương pháp 4.
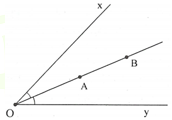
Nếu tia OA và tia OB là hai tia phân giác của góc xOy thì ba điểm O; A; B thẳng hàng.
(Cơ sở của phương pháp này là: Mỗi góc khác góc bẹt có một và chỉ một tia phân giác).
* Hoặc: Hai tia OA và OB cùng nằm trên nửa mặt phẳng bờ chứa tia Ox, \( \widehat{xOA} = \widehat{xOB} \) thì ba điểm O, A, B thẳng hàng.

5. Phương pháp 5.
Nếu K là trung điểm BD, K’ là giao điểm của BD và AC. Nếu K’ là trung điểm BD thì K’ ≡ K và A, K, C thẳng hàng.
(Cơ sở của phương pháp này là: Mỗi đoạn thẳng chỉ có một trung điểm).

B. Bài tập

Bài 1. Cho tam giác ABC vuông ở A, M là trung điểm AC. Kẻ tia Cx vuông góc CA (tia Cx và điểm B ở hai nửa mặt phẳng đối nhau bờ AC). Trên tia Cx lấy điểm D sao cho CD = AB. Chứng minh ba điểm B, M, D thẳng hàng.

Bài 2. Cho hai đoạn thẳng AC và BD cắt nhau tại trung điểm O của mỗi đoạn. Trên tia AB lấy điểm M sao cho B là trung điểm AM, trên tia AD lấy điểm N sao cho D là trung điểm AN. Chứng minh ba điểm M, C, N thẳng hàng.

Bài 3. Cho tam giác ABC cân ở A. Trên cạnh AB lấy điểm M, trên tia đối tia CA lấy điểm N sao cho BM = CN. Gọi K là trung điểm MN. Chứng minh ba điểm B, K, C thẳng hàng.

Bài 4. Cho tam giác ABC cân ở A, \( \widehat{BAC} = 108^\circ \). Gọi O là một điểm nằm trên tia phân giác của góc C sao cho \( \widehat{CBO} = 12^\circ \). Vẽ tam giác đều BOM (M và A cùng thuộc một nửa mặt phẳng bờ BO). Chứng minh ba điểm C, A, M thẳng hàng.

Bài 5. Cho tam giác ABC vuông tại A và \( \widehat{B} = 60^\circ \). Vẽ tia Cx ⟂ BC và lấy CE = CA (CE và CA cùng phía với BC). Trên tia đối của tia BC, lấy điểm F sao cho BF = BA. Chứng minh rằng:

a) \( \Delta ACE \) đều;

b) E, A, F thẳng hàng.

Bài 6. Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA, lấy điểm E sao cho ME = MA.

a) Chứng minh rằng \( AC = EB \) và \( AC \parallel BE \).

b) Gọi I là một điểm trên AC; K là một điểm trên EB sao cho AI = EK. Chứng minh ba điểm I, M, K thẳng hàng.

Bài 7. Cho \( \triangle ABC \) cân tại A, có \( \widehat{A} < 90^\circ \). Kẻ BD vuông góc với AC, kẻ CE vuông góc với AB. Gọi K là giao điểm của BD và CE. Chứng minh rằng:

a) \( \triangle BCE = \triangle CBD \);

b) \( \triangle BEK = \triangle CDK \);

c) AK là phân giác góc BAC;

d) Ba điểm A, K, I thẳng hàng (với I là trung điểm BC).

Bài 8. Cho \( \triangle ABC \) có AB < AC. Kẻ tia phân giác AD của \( \widehat{BAC} \) (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng:

a) \( \triangle BDF = \triangle EDC \);

b) F, D, E thẳng hàng;

c) \( AD \perp FC \).

Bài 9. Cho tam giác ABC vuông cân tại A. Vẽ ra phía ngoài tam giác ABC tam giác BCM cân tại M có góc ở đáy là \( 15^\circ \). Trên nửa mặt phẳng bờ AB chứa điểm C, vẽ tam giác đều ABN. Chứng minh ba điểm B, M, N thẳng hàng.

Bài 10. Cho tam giác ABC. Vẽ về phía ngoài tam giác ABC các tam giác vuông tại A là \( \triangle ADB \), \( \triangle ACE \) có \( AB = AD,~ AC = AE \). Kẻ AH vuông góc BC; DM vuông góc AH và EN vuông góc AH. Chứng minh rằng:

a) \( DM = AH \).

b) Gọi I là trung điểm của MN. Chứng minh rằng D, I, E thẳng hàng.