
Tiếp tục với chủ đề "ôn thi học sinh giỏi toán lớp 5", sau đây MATHX xin gửi tới phụ huynh và các em học sinh phần 2 của bài viết 50 bài toán chọn lọc bồi dưỡng ôn thi học sinh giỏi toán lớp 5. Để theo dõi phần 1, phụ huynh và các em học sinh truy cập vào link ở phía bên dưới. Chúc các em ôn tập hiệu quả và đạt nhiều thành tích cao trong các kì thi!
50 BÀI TOÁN CHỌN LỌC BỒI DƯỠNG ÔN THI HỌC SINH GIỎI KÈM LỜI GIẢI CHI TIẾT (PHẦN 1) - TOÁN LỚP 5
Lời giải :
Với bài toán này có rất nhiều cách để làm. Sau đây thầy cô Mathx sẽ giới thiệu tới các em 3 cách.
Cách 1: Nhát thứ nhất chia đôi theo bề dầy của chiếc bánh và để nguyên vị trí này cắt thêm 3 nhát (như hình vẽ).

Lưu ý là AM = BN = DQ = CP = 1/6 AB và IA = ID = KB = KC = 1/2 AB.
Các bạn có thể dễ dàng chứng minh được 12 miếng bánh là bằng nhau và cả 3 nhát cắt đều đi qua đúng ... tâm bánh.
Cách 2: Cắt 2 nhát theo 2 đường chéo để được 4 miếng rồi chồng 4 miếng này lên nhau cắt 2 nhát để chia mỗi miếng thành 3 phần bằng nhau (lưu ý: BM = MN = NC).
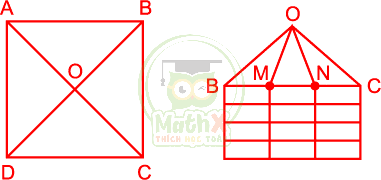
Cách 3: Nhát thứ nhất cắt như cách 1 và để nguyên vị trí này để cắt thêm 3 nhát như hình vẽ.
Lưu ý: AN = AM = CQ = CP = 1/2 AB.
Lời giải :
Tổng các số trên ba đỉnh của mỗi hình tam giác là 1 + 2 + 3 = 6.
Tổng này là một số chia hết cho 6.
Khi chồng các hình tam giác này lên nhau sao cho không có chữ số nào bị che lấp, rồi tính tổng tất cả các chữ số nhìn thấy được phải có kết quả là số chia hết cho 6.
Vì số 2002 không chia hết cho 6 nên bạn đó đã tính sai.
Lời giải :
Tổng các số từ 1 đến 12 là: (12+1) x 12 : 2 = 78
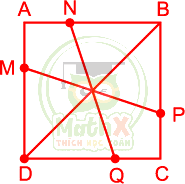
Vì tổng 4 số cùng nằm trên một cột hay một hàng đều như nhau nên tổng số của 4 hàng và cột phải là một số chia hết cho 4. Đặt các chữ cái A, B, C, D vào các ô vuông ở giữa (hình vẽ).

Khi tính tổng số của 4 hàng và cột thì các số ở các ô A, B, C, D được tính hai lần. Do đó để tổng 4 hàng, cột chia hết cho 4 thì tổng 4 số của 4 ô A, B, C, D phải chia cho 4 dư 2 (vì 78 chia cho 4 dư 2). Ta thấy tổng của 4 số có thể là: 10, 14, 18, 22, 26, 30, 34, 38, 42.
Ta xét một vài trường hợp:
1) Tổng của 4 số bé nhất là 10. Khi đó 4 số sẽ là 1, 2, 3, 4. Do đó tổng của mỗi hàng (hay mỗi cột) là: (78 + 10) : 4 = 22. Ta có cách điền như hình dưới:

2) Tổng của 4 số là 14. Ta có:
14 = 1 + 2 + 3 + 8 = 1 + 2 + 4 + 7 = 1 + 3 + 4 + 6 = 2 + 3 + 4 + 5.
Do đó tổng của mỗi hàng (hay mỗi cột) là: (78 + 14) : 4 = 23.
Ta có cách điền như hình sau:

Các trường hợp còn lại sẽ cho ta kết quả ở mỗi hàng (hay mỗi cột) lần lượt là 24, 25, 26, 27, 28, 29, 30. Ngoài ra còn có rất nhiều cách điền khác nữa đấy, Mathx sẽ để các em tự thử làm nhé.
Lời giải :
Gọi số học sinh đạt giải cả 3 môn là a (học sinh)
Gọi số học sinh đạt giải cả 2 môn là b (học sinh)
Gọi số học sinh chỉ đạt giải 1 môn là c (học sinh)
Tổng số giải đạt được là:
3 x a + 2 x b + c = 15 (giải).
Vì tổng số học sinh đạt 3 giải, 2 giải, 1 giải tăng dần nên a < b < c.
Vì bất kỳ 2 môn nào cũng có ít nhất 1 học sinh đạt giải cả 2 môn nên:
- Có ít nhất 1 học sinh đạt giải cả 2 môn Văn và Toán.
- Có ít nhất 1 học sinh đạt giải cả 2 môn Toán và Ngoại Ngữ.
- Có ít nhất 1 học sinh đạt giải cả 2 môn Văn và Ngoại Ngữ.
Do vậy b= 3.
Giả sử a = 2 thì b bé nhất là 3, c bé nhất là 4; do đó tổng số giải bé nhất là:
3 x 2 + 2 x 3 + 4 = 16 > 15 (loại). Do đó a < 2, nên a = 1.
Ta có: 3 x 1 + 2 x b + c = 15 suy ra: 2 x b + c = 12.
Nếu b = 3 thì c = 12 - 2 x 3 = 6 (đúng).
Nếu b = 4 thì c = 12 - 2 x 4 = 4 (loại vì trái với điều kiện b < c)
Vậy có 1 bạn đạt 3 giải, 3 bạn đạt 2 giải, 6 bạn đạt 1 giải.
Đội tuyển đó có số học sinh là:
1 + 3 + 6 = 10 (bạn).
Lời giải :
Các em có thể xét các tổng theo từng hàng, từng cột và không khó khăn lắm sẽ có kết quả sau:

Lời giải :
Tổng khối lượng dưa là:
1 x 65 + 2 x 35 + 3 x 15 = 180 (kg).
Giả sử khối lượng dưa ở mỗi giỏ khác nhau thì tổng khối lượng dưa ở 20 giỏ bé nhất là:
1 + 2 + 3 + ... + 19 + 20 = 210 (kg).
Vì 210 kg > 180 kg nên chắc chắn phải có ít nhất 2 giỏ trong 20 giỏ có khối lượng bằng nhau. Vậy Trí đã nói đúng.
Lời giải :
Vì Hoàng và Hùng góp số vở của mình với số vở của Sơn, rồi chia đều cho nhau, nên tổng số vở của ba bạn là một số chia hết cho 3. Số vở của Hoàng và Hùng đều chia hết cho 3 nên số vở của Sơn cũng là số chia hết cho 3.
Số vở của Sơn phải ít hơn 6 vì nếu số vở của Sơn bằng hoặc nhiều hơn số vở của Hoàng (6 quyển) thì sau khi góp vở lại chia đều Sơn sẽ không phải trả thêm 800 đồng. Số vở của Sơn khác 0 (Sơn phải có vở của mình thì mới góp chung với các bạn được chứ!), nhỏ hơn 6 và chia hết cho 3 nên Sơn có 3 quyển vở.
Số vở của mỗi bạn sau khi chia đều là: (6 + 3 + 3) : 3 = 4 (quyển)
Như vậy Sơn được các bạn đưa thêm: 4 - 3 = 1 (quyển)
Giá tiền một quyển vở là 800 đồng.

Lời giải :
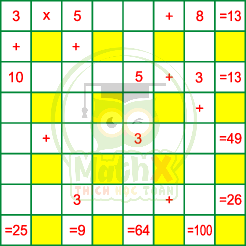
Đặt các chữ cái vào các ô trống:

Theo đầu bài ta có các chữ cái khác nhau biểu thị các số khác nhau. Do đó: a ≠ 1; c ≠ 1; d ≠ 1; b > 1; e > 1. Vì 9 = 1 x 9 = 3 x 3 nên b ≠ 9 và e ≠ 9; và 7 = 1 x 7 nên b ≠ 7 và e ≠ 7.
Do đó: b = 6 và e = 8 hoặc b = 8 và e = 6.
Vì 6 = 2 x 3 và 8 = 2 x 4 nên a = b : c = e : d = 2.
Trong các ô trống a, b, c, d, e đã có các số 2, 3, 4, 6, 8; do đó chỉ còn các số 1, 5, 7, 9 điền vào các ô trống g, h, i, k.
* Nếu e = 6 thì g = 7 và h = 1. Do đó a = i - k = 9 - 5 = 42 (loại).
* Nếu e = 8 thì g = 9 và h = 1. Do đó a = i - k = 7 - 5 = 2 (đúng). Khi đó: b = 6 và c = 3.
Kết quả:


Lời giải :
Bài toán có rất nhiều cách đặt dấu phép tính và dấu ngoặc. Xin nêu một số cách:
Cách 1: (123 + 4 x 5) x (6 + 7 - 8 + 9 + 1 - 2 - 3 + 4) = 2002
Cách 2: (1 x 2 + 3 x 4) x (5 + 6) x [(7 + 8 + 9) - (1 + 2 x 3 + 4)] = 2002
Cách 3: (1 + 2 + 3 + 4 x 5) x (6 x 7 + 8 + 9 - 1 + 23 - 4) = 2002
Lời giải :
Vì số 18 và số 12 đều chia hết cho 3, nên tổng số tiền mua 18 gói bánh và 12 gói kẹo phải là số chia hết cho 3.
Vì Huy đưa cho cô bán hàng 2 tờ 100000 đồng và được trả lại 72000 đồng, nên số tiền mua 18 gói bánh và 12 gói kẹo là:
100000 x 2 - 72000 = 128000 (đồng).
Vì số 128000 không chia hết cho 3, nên bạn Nam nói “Cô tính sai rồi” là đúng.
Lời giải :
Ta có nhiều cách để đo được 9 phút:
Cách 1: Bạn có thể cho cả 2 cái đồng hồ cát cùng chảy một lúc và chảy hết cát 3 lần. Khi đồng hồ 4 phút chảy hết cát 3 lần (4 x 3 = 12(phút)) thì bạn bắt đầu tính thời gian, từ lúc đó đến khi đồng hồ 7 phút chảy hết cát 3 lần thì vừa đúng được 9 phút (7 x 3 - 12 = 9(phút));
Cách 2: Cho cả hai đồng hồ cùng chảy một lúc, đồng hồ 7 phút chảy hết cát một lần (7 phút), đồng hồ 4 phút chảy hết cát 4 lần (16 phút). Khi đồng hồ 7 phút chảy hết cát ta bắt đầu tính thời gian, từ lúc đó đến lúc đồng hồ 4 phút chảy hết cát 4 lần là vừa đúng 9 phút (16 - 7 = 9 (phút)); ...
Lời giải :
- Vì A≠G mà chữ số hàng chục của tổng là 0 nên phép cộng có nhớ 1 sang hàng trăm nên ở hàng trăm: H + N + 1 (nhớ) = 10; nhớ 1 sang hàng nghìn. Do đó H + N = 10 - 1 = 9.
- Phép cộng ở hàng nghìn: N + 1 (nhớ) = 2 nên N = 2 - 1 = 1.
Thay N = 1 ta có: H + 1 = 9 nên H = 9 - 1 = 8
- Phép cộng ở hàng đơn vị: Có 2 trường hợp xảy ra:
* Trường hợp 1: Phép cộng ở hàng đơn vị không nhớ sang hàng chục.
Khi đó: M + O = 0 và A + G = 10.
Ta có bảng: (Lưu ý 4 chữ M, O, A, G phải khác nhau và khác 1; 8)
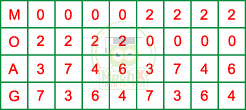
* Trường hợp 2: Phép cộng ở hàng đơn vị có nhớ 1 sang hàng chục.
Khi đó: M + O = 12 và A + G = 9. Ta có bảng:

Vậy bài toán có 24 đáp số như trên.

Lời giải :
Ta có ba cách giải cơ bản sau:

Từ ba cách giải cơ bản này ta có thể tạo nên nhiều phương án khác nữa, chẳng hạn:

Lời giải :
* Biển số 39A 0452. Ta có một số cách sau:
(4 x 2 - 5 + 0) x 3 = 9
5 x 2 - 4 + 3 + 0 = 9
45 : 9 - 3 - 2 = 0
(9 + 2 - 3) x 5 = 40
(4 + 5) : 9 + 2 + 0 = 3
9 : 3 - ( 5 - 4 + 2) = 0
3 - 9 : (4 + 5) - 0 = 2
9 : (4 + 5) + 2 + 0 = 3
(9 + 5) : 2 - 4 + 0 = 3
9 + 3 : (5 - 2) + 0 = 4
5 + 2 - 9 : 3 - 0 = 4
(9 : 3 + 0) + 4 - 2 = 5
(9 + 3) : 4 + 0 + 2 = 5 . . . .
* Biển số 38B 0088. Có nhiều lời giải dựa vào tính chất “nhân một số với số 0”
38 x 88 x 0 = 0
hoặc tính chất “chia số 0 cho một số khác 0”
0 : (38 + 88) = 0
Một vài cách khác:
(9 - 8) + 0 - 8 : 8 = 0
8 : 8 + 8 + 0 + 0 = 9 . . . .
* Biển số 52N 8233. Ta có một số cách sau:
5 x 2 - 8 + 3 - 3 = 2
8 : (5 x 2 - 3 - 3) = 2
[(23 - 3) : 5] x 2 = 8
(5 + 2 + 2) - (3 : 3) = 8
(8 : 2 - 3) x (3 + 2) = 5
[(8 + 2) x 3 : 3] : 2 = 5
(5 x 2 + 3 + 3) : 2 = 8
3 x 3 - 5 + 2 + 2 = 8 . . . .
Lời giải :
Với một chiếc đồng hồ đang hoạt động bình thường, cứ mỗi giờ trôi qua thì kim phút quay được một vòng, còn kim giờ quay được \(\dfrac {1}{12}\) vòng.
Hiệu vận tốc của kim phút và kim giờ là:
\(1 - \dfrac {1}{12} = \dfrac {11}{12}\) (vòng/giờ)
Thời gian để hai kim trùng nhau một lần là:
\(1 : \dfrac {11}{12} = \dfrac {12}{11}\) (giờ)
Vậy sau 24 giờ hai kim sẽ trùng nhau số lần là :
\(24 : \dfrac {12}{11} = 22\) (lần).
Lời giải :
Vì két chỉ mở được nếu có mặt ít nhất hai người, nên số ổ khoá phải lớn hơn hoặc bằng 2.
a) Làm 2 ổ khoá.
+ Nếu làm 3 chìa thì sẽ có hai người có cùng một loại chìa; hai người này không mở được két.
+ Nếu làm nhiều hơn 3 chìa thì ít nhất có một người cầm 2 chìa khác loại; chỉ cần một người này đã mở được két.
Vậy không thể làm 2 ổ khoá.
b) Làm 3 ổ khoá
+ Nếu làm 3 chìa thì cần phải có đủ ba người mới mở được két.
+ Nếu làm 4 chìa hoặc 5 chìa thì ít nhất có hai người không mở được két.
+ Nếu làm 6 chìa (mỗi khoá 2 chìa) thì mỗi người cầm hai chìa khác nhau thì chỉ cần hai người bất kỳ là mở được két.
Vậy ít nhất phải làm 3 ổ khoá và mỗi ổ khoá làm 2 chìa.
Lời giải :
Bài Toán này có nhiều cách làm, Mathx sẽ đưa ra cho các em sơ sơ 3 cách làm. Các e sắp xếp theo như hình vẽ bên dưới

Lời giải :
Vì chỉ có 25 người, mà trong đó có 20 ít hơn 30 tuổi và 15 người nhiều hơn 25 tuổi, nên số người được điểm 2 lần là:
(20 + 15) - 25 = 10 (người)
Đây chính là số người có độ tuổi ít hơn 30 tuổi và nhiều hơn 20 tuổi (từ 21 tuổi đến 29 tuổi).

Số người từ 30 tuổi trở lên là:
25 - 20 = 5 (người)
Số người từ 20 tuổi trở xuống là:
25 - 15 = 10 (người)
Số người ít hơn 30 tuổi là:
10 + 10 = 20 (người)
Số người nhiều hơn 20 tuổi là:
10 + 5 = 15 (người)
Vậy có thể có 20 người dưới 30 tuổi và 15 người trên 20 tuổi; trong đó từ 21 đến 29 tuổi ít nhất có hai người cùng độ tuổi.
Lời giải :
Giả sử cả 4 số đều là 10 thì tích là 10 x 10 x 10 x 10 = 10000 mà 10000 > 3024 nên cả 4 số tự nhiên liên tiếp đó phải bé hơn 10.
Vì 3024 có tận cùng là 4 nên cả 4 số phải tìm không thể có tận cùng là 5. Do đó cả 4 số phải hoặc cùng bé hơn 5, hoặc cùng lớn hơn 5.
Nếu 4 số phải tìm là 1; 2; 3; 4 thì:
1 x 2 x 3 x 4 = 24 < 3024 (loại)
Nếu 4 số phải tìm là 6; 7; 8; 9 thì:
6 x 7 x 8 x 9 = 3024 (đúng)
Vậy 4 số phải tìm là 6; 7; 8; 9.
Lời giải :
Một hình chữ nhật có chiều dài (a) và chiều rộng (b) đều là số tự nhiên (cùng một đơn vị đo) thì chu vi (P) của hình đó phải là số chẵn:
P = (a + b) x 2
Tổng độ dài của tất cả các que là:
1 x 16 + 2 x 20 + 3 x 25 = 131 (cm)
Vì 131 là số lẻ nên không thể xếp tất cả các que đó thành một hình chữ nhật được.
Lời giải :
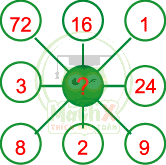
Để cho gọn, ta ký hiệu các số trên những ô tròn theo bảng sau:

Lấy A chia cho K: 72 : 9 = 8
Lấy G chia cho C: 8 : 1 = 8
Lấy B chia cho H: 16 : 2 = 8
Lấy E chia cho D: 24 : 3 = 8
Ta thấy kết quả ở ô "Đ" đều bằng 8. Vậy (?) là 8.
Bài 47: Cô giáo yêu cầu: “Các con lấy 6 điểm trên một đường tròn, nối các điểm đó bởi các đoạn thẳng tô bởi mực xanh hoặc mực đỏ”. Bạn lớp trưởng tập hợp các hình vẽ lại và xem, bạn thốt lên: “Bạn nào cũng vẽ được 1 tam giác mà 3 cạnh cùng màu mực”! Bạn hãy thử làm lại xem. Ai có thể lập luận để làm rõ tính chất này?
Lời giải :
Bài toán này ta cũng có nhiều cách giải, đây là một trong các cách giải bài này: Ta gọi 6 điểm nằm trên đường tròn là A1, A2, A3, A4, A5, A6. Bằng bút xanh và đỏ ta nối A1 với 5 điểm còn lại ta được 5 đoạn thẳng có hai màu xanh hoặc đỏ.

Theo nguyên lý Điríchlê có ít nhất 3 đoạn thẳng cùng màu.
Không làm mất tính tổng quát, ta nối 3 đoạn A1A2, A1A3, A1A4 bằng bút màu đỏ.
Ta nối tiếp A2A4 và A2A3.
Để tam giác A1A2A3 và tam giác A1A2A4 có 3 cạnh không cùng màu thì A2A4 và A2A3 phải tô màu xanh.
Bây giờ ta tiếp tục nối A3A4, ta thấy A3A4 được tô bằng bất kỳ màu xanh hoặc đỏ thì ta cũng được ít nhất một tam giác có 3 cạnh cùng màu (hoặc A1A3A4 có 3 cạnh đỏ hoặc A2A3A4 có 3 cạnh màu xanh).
Lời giải :
Số viên đạn Dũng đã bắn phải ít hơn 13 viên (vì nếu Dũng bắn 13 viên thì Dũng được số điểm ít nhất là: 8 x 11 + 9 x 1 + 10 x 1 = 107 (điểm) > 100 điểm, điều này vô lý).
Theo đề bài Dũng đã bắn hơn 11 viên nên số viên đạn Dũng đã bắn là 12 viên.
Mặt khác 12 viên đều trúng vào các vòng 8, 9, 10 điểm nên ít nhất có 10 viên vào vòng 8 điểm, 1 viên vào vòng 9 điểm, 1 viên vào vòng 10 điểm.
Do đó số điểm Dũng bắn được ít nhất là:
8 x 10 + 9 x 1 + 10 x 1 = 99 (điểm)
Số điểm hụt đi so với thực tế là:
100 - 99 = 1 (điểm)
Như vậy sẽ có 1 viên không bắn vào vòng 8 điểm mà bắn vào vòng 9 điểm; hoặc có 1 viên không bắn vào vòng 9 điểm mà bắn vào vòng 10 điểm.
Nếu có 1 viên Dũng không bắn vào vòng 9 điểm mà bắn vào vòng 10 điểm thì tổng cộng sẽ có 10 viên vào vòng 8 điểm và 2 viên vào vòng 10 điểm (loại vì không có viên nào bắn vào vòng 9 điểm).
Vậy sẽ có 1 viên không bắn vào vòng 8 điểm mà bắn vào vòng 9 điểm, tức là có 9 viên vào vòng 8 điểm, 2 viên vào vòng 9 điểm và 1 viên vào vòng 10 điểm.
Lời giải :
Đây là một bài toán lôgíc cơ bản và khó.
Ta ký hiệu theo thứ tự “đi xem” ca nhạc: n (Bà nội), m (mẹ), b (Bố), C (Chi) và B (Bảo) và năm người trên khi họ “không đi” là n, m, b, C và B.
Như vậy theo ý kiến của năm người là:
a) n và m
b) b và m
c) b và n
d) n và C
e) b và B.
Cần phải nhấn mạnh rằng: Mỗi trong năm ý trên đều có một phần đúng và một phần sai (trừ ý của bà!).
Câu mà bà nội nói là đúng với cả năm ý trên.
- Nếu chọn câu a) thì không có e tức b và B.
- Nếu chọn câu b) thì không có d tức n và C.
- Nếu chọn câu c) thì các ý kiến khác có một phần đúng. Bà nội đã nói câu c)
Lời giải :
Giả sử rằng A và B tham gia cuộc chơi mà A lấy diêm trước.
Để chắc thắng thì trước lần cuối cùng A phải để lại 5 que diêm, trước đó A phải để lại 10 que diêm và lần bốc đầu tiên A để lại 15 que diêm, khi đó dù B có bốc bao nhiêu que thì vẫn còn lại số que để A chỉ cần bốc một lần là hết.
Muốn vậy thì lần trước đó A phải để lại 10 que diêm , khi đó dù B bốc bao nhiêu que vẫn còn lại số que mà A có thể bốc để còn lại 5 que .
Tương tự như thế thì lần bốc đầu tiên A phải để lại 15 que diêm . Với " chiến lược" này bao giờ A cũng là người thắng cuộc.
Trên đây là toàn bộ nội dung về chủ đề các bài toán chọn lọc ôn thi học sinh giỏi lớp 5. Phụ huynh và các em học sinh tham khảo thêm một số nội dung về toán lớp 5 tại đây:
TÓM TẮT TỔNG HỢP KIẾN THỨC HÌNH HỌC - TOÁN LỚP 5
10 DẠNG TOÁN VỀ DÃY SỐ VÀ PHƯƠNG PHÁP GIẢI (PHẦN 1) - TOÁN LỚP 5
ĐÁP ÁN - ĐỀ GIAO LƯU TOÁN TUỔI THƠ LỚP 5 - CẤP THÀNH PHỐ 2024 - MATHX