
Nhằm giúp các em học sinh có cái nhìn tổng quan về nội dung và khối lượng kiến thức trong chương trình hình học áp dụng ở khối tiểu học. Bài viết này MATHX tổng hợp đến các em kiến thức hình học toán lớp 5 chi tiết nhất. Mời các em cùng tham khảo
Ngoài ra PHHS tham khảo thêm một số tài liệu ôn thi lớp 5 tại đây:
10 ĐỀ THI CUỐI HỌC KÌ II TOÁN LỚP 5
ÔN TẬP VÀ BỔ SUNG VỀ GIẢI TOÁN - TOÁN LỚP 5
1. Tính chất: Hình bình hành có hai cặp cạnh đối diện song song và bằng nhau.
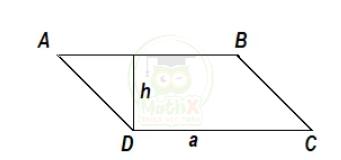
Kí hiệu: Đáy là a, chiều cao là h.
2. Tính chu vi: Chu vì hình bình hành là tổng độ dài của 4 cạnh.
3.Tính diện tích: Muốn tính diện tích hình bình hành, ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo).
| S = a x h |
Muốn tìm độ đài đáy, ta lấy diện tích chia cho chiều cao.
| a = S : b |
Muốn tìm chiều rộng, ta lấy diện tích chia cho chiều dài.
| b = S : a |
1.Tính chất:
Hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau
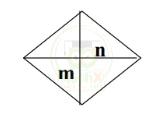
Hình thoi có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
Kí hiệu hai đường chéo là m và n
2.Tính chu vi: Muốn tính chu vi hình thoi, ta lấy số đo một cạnh nhân với 4.
3.Tính diện tích: Diện tích hình thoi bảng tích của độ dài hai đường chéo chia cho 2 (cùng đơn vị đo).
| S = \(\dfrac {m \times n} {2}\) |
1.Tính chất: Hình thang có một cặp cạnh đối diện song song.
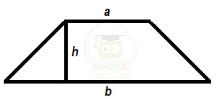
- Chiều cao: là đoạn thăng ở giữa hai đáy và vuông góc với hai đáy
Kí hiệu:
Đáy lớn là a
Đáy nhỏ là b
Chiều cao là h
2.Tính diện tích: Muốn tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho 2.
| S = (a + b) x h : 2 |
Hoặc: Muốn tính diện tích hình thang ta lấy trung bình cộng hai đáy nhân với chiều cao.
| S = \(\dfrac {a + b} {2}\) x h |
Tính tổng hai đáy: Ta lấy diện tích nhân với 2 rồi chia cho chiều cao.
| (a + b) = S x 2 : h |
Tính độ dài đáy lớn: Ta lấy diện tích nhân với 2, chia cho chiều cao rồi trừ đi độ dài đáy bé.
| a = S x 2 : h - b |
Tính độ dài đáy bé: Ta lấy diện tích nhân với 2, chia cho chiều cao rồi trừ đi độ dài đáy lớn.
| b = S x 2 : h - a |
Tính chiều cao: Ta lấy diện tích nhân với 2 rồi chia cho tổng độ dài hai đáy.
| h = S x 2 : (a + b) |
Hoặc: Tính chiều cao: Ta lấy diện tích chia cho trung bình cộng của hai đáy.
| h = S : \(\dfrac {a + b} {2}\) |
1.Tính chất: Hình tam giác có ba cạnh, 3 góc, 3 đỉnh.
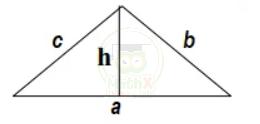
Chiều cao là đoạn thẳng hạ từ đỉnh vuông góc với cạnh đối diện.
Kí hiệu đáy là a, chiều cao là h
2.Tính chu vi: Chu vi hình tam giác là tổng độ dài của 3 cạnh.
|
P = a + b + c |
3.Tính diện tích: Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho 2.
| S = a x h : 2 |
Tính cạnh đáy: Ta lấy diện tích nhân với 2 rồi chia cho chiều cao.
| a = S x 2 : h |
Tính chiều cao: Ta lấy diện tích nhân với 2 rồi a chia cho cạnh đáy.
| h = S x 2 : a |
1.Tính chất: Hình tròn có tất cả các bán kính bằng nhau.
Đường bao quanh hình tròn gọi là đường tròn.
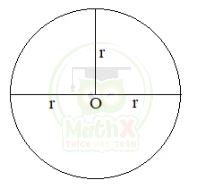
Điểm chính giữa hình tròn là tâm kí hiệu là O.
Đoạn thẳng nối tâm với một điểm trên đường tròn gọi là bán kính. Kí hiệu là r.
Đoạn thẳng đi qua tâm và nối hai điểm của đường tròn gọi là đường kính. Kí hiệu là d
Đường kính gấp hai lần bán kính.
| d = 2 x r |
2. Tính chu vi: Muốn tính chu vi hình tròn ta lấy đường kính nhân với số 3,14.
| C = d x 3,14 |
Hoặc ta lấy bán kính nhân 2 rồi nhân với số 3,14.
| C = r x 2 x 3,14 |
Tính đường kính: ta lấy chu vi chia cho 2 rồi chia cho số 3,14.
| d = C : 3,14 |
Tính bán kính: ta lấy chu vi chia cho 2 rồi chia cho số 3,14.
| r = C : 2 : 3,14 |
3. Tính diện tích: Muốn tích diện tích hình tròn ta lấy bán kính nhân với bán kính rồi nhân với 3,14.
| S = r x r x 3,14 |
Biết diện tích, muốn tìm bán kính, ta làm như sau:
Lấy diện tích chia cho số 3,14 để tìm tích của hai bán kính, rồi tìm xem số nào đó nhân với chính nó bằng tích đó thì đấy là bán kính hình tròn
VD: Cho diện tích một hình tròn bằng 28,26 \(cm^2\). Tìm bán kính hình tròn đó.
Giải: Tích hai bán kính hình tròn là:
28,26 : 3,14 = 9 (\(cm^2\))
Vì 9 = 3 x 3 nên bán kính hình tròn là 3cm
ìt có 6 mặt, Hai mặt đáy và bốn mặt bên.
1.Tính chất: Hình hộp chữ nhật có 6 mặt, Hai mặt đáy và bốn mặt bên.
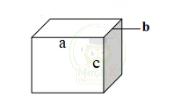
- Có 8 đỉnh, 12 cạnh
- Có ba kích thước:
dài (a), z
chiều rộng (b)
chiều cao (c).
2.Tính diện tích xung quanh: Muốn tính diện tích xung quanh hình hộp chữ nhật ta lấy chu vi đáy nhân với chiểu cao (cùng một đơn vị đo).
| Sxq = P(đáy) x c = (a + b) x 2 x c |
Muốn tìm chu vi đáy, ta lấy diện tích xung quanh chia cho chiều cao.
| P(đáy) = Sxq : c |
Muốn tìm chiều cao, ta lấy diện tích xung quanh chia cho chu vi đáy.
| c = Sxq : P(đáy) |
Muốn tìm tổng hai đáy, ta lây diện tích xung quanh chia cho 2 rồi chia cho chiều cao.
| (a + b) = Sxq : 2 : h |
Muốn tìm chiều dài, ta lấy diện tích xung quanh chia cho 2, chia cho chiều cao rồi trừ đi chiều rộng.
| a = Sxq : 2 : c - b |
Muốn tìm chiều rộng, ta lấy diện tích xung quanh chia cho 2, chia cho chiều cao rồi trừ đi chiều dài.
| b = Sxq : 2 : c - a |
3.Tính diện tích toàn phần: Muốn tính diện tích toàn phần hình hộp chữ nhật ta lấy diện tích xung quanh cộng diện tích hai đáy.
| Stp = Sxq + S(2đáy) = (a + b) x 2 x c +a x b x 2 |
Muốn tìm diện tích đáy ta lấy chiêu dài nhân với chiều rộng.
| S(đáy) = a x b |
Muốn tìm chiều đài, ta lấy diện tích đáy chia cho chiều rộng.
| b = S(đáy) : b |
Muốn tìm chiều rộng, ta lấy diện tích đáy chia cho chiều dài.
| b = S(đáy) : a |
4.Tính thể tích hình hộp chữ nhật: ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng một đơn vị đo).
| V = a x b x c |
Muốn tìm chiều dài, ta lấy thể tích chia cho chiều rộng rồi chia tiếp cho chiều cao.
| a = V : b : c |
Muốn tìm chiều rộng, ta lấy thể tích chia cho chiều dài rồi chia tiếp cho chiều cao.
| b = V : a : c |
Muốn tìm chiều cao, ta lấy thể tích chia cho chiều dài rồi chia tiếp cho chiều rộng.
| c = V : a : b = S(đáy) |
1.Tính chất: Hình lập phương có 6 mặt là các hình vuông bằng nhau.
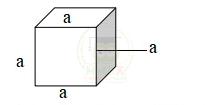
Có 8 đỉnh, 12 cạnh dài bằng nhau.
Kí hiệu cạnh là a
2.Tính diện tích xung quanh: Muốn tính diện tích xung quanh hình lập phương ta lấy diện tích một mặt nhân với 4.
| Sxq = S(1 mặt) x 4 |
3.Tính diện tích toàn phần: Muốn tính diện tích toàn phần hình lập phương ta lấy diện tích một mặt nhân với 6.
| Stp = S(1 mặt) x 6 |
Muốn tìm điện tích một mặt ta lấy diện tích xung quanh chia cho 4 hoặc diện tích toàn phần chia cho 6.
| S(1 mặt) = Sxq : 4 = Stp : 6 |
Muốn tìm 1 cạnh hình lập phương, ta tìm xem một số nào đó nhân với chính nó bằng diện tích một mặt, thì đó là cạnh.
VD: Cho diện tích một mặt là 25 \(m^2\). Tìm cạnh của hình lập phương đó.
Giải:
Ta có 25 = 5 x 5;
Vậy cạnh hình lập phương là 5m
4.Tính thể tích hình lập phương: ta lấy cạnh nhân với cạnh rồi nhân với cạnh.
| V = a x a x a |
Muốn tìm 1 cạnh hình lập phương, ta tìm xem một số nào đó nhân với chính nó rồi nhân tiếp với nó bằng thể tích, thì đó là cạnh.
VD: Cho thể tích là 125 \(m^2\). Tìm cạnh của hình lập phương đó.
Giải:
Ta có 25 = 5 x 5 x 5;
Vậy cạnh hình lập phương là 5m
Trên đây là nội dung ôn tập tổng hợp kiến thức hình học lớp 5. Ngoài ra để học thêm kiến thức nâng cao về hình học, các em học sinh tham khảo các bài toán nâng cao lớp 5 và cách giải trên website của MATHX.VN