Trường Toán Online MATHX
Bộ 5 đề kiểm tra giữa kì 2 Toán 9 năm 2023 được MATHX biên soạn nhằm giúp học sinh ôn lại kiến thức và rèn kĩ năng giải bài tập để các em đạt kết quả cao hơn trong kì thi kiểm tra giữa kì 2 sắp tới. Chúc các em học tốt.
Phụ huynh và các em học sinh xem thêm đề thi giữa kì 2 môn toán lớp 9 năm học 2023 - 2024 tại đây:
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 1
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 2
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 3
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 4
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 9 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 5
Câu 5: Phương trình \(m x^{2}-2x+1=0\) (m là tham số) có hai nghiệm phân biệt khi và chỉ khi:
A. m < 1
B. m > 1
C. m < 1 và m ≠ 0
D. m ≠ 0
Câu 6: Số tiếp tuyến chung của hai đường tròn tiếp xúc ngoài là
Câu 1: 1) Trong mặt phẳng tọa độ Oxy, vẽ đồ thị hàm số \(y={\dfrac{1}{2}}x^2\)
2) Trên đồ thị hàm số \(y={\dfrac{1}{2}}x^2\) lấy điểm A có hoành độ bằng 2 và điểm B có tung độ bằng 2 (điểm B khác điểm A). Hãy viết phương trình đường thẳng AB và chứng minh ΔOAB cân.
Lời giải:
1) Ta có bảng giá trị:
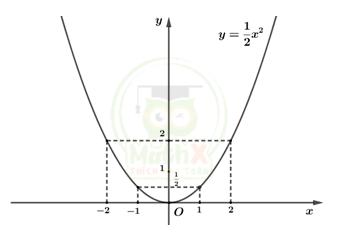
=> Đồ thị hàm số \(y={\dfrac{1}{2}}x^2\) là đường cong Parabol đi qua các điểm có tọa độ \((-2\,;\;2)\;,(-1\,;\;\frac{1}{2})\;,(0\,;\,0)\;,\;(\dfrac{1}{2}\,;\;1)\;,(2\,;\;2).\)
2)
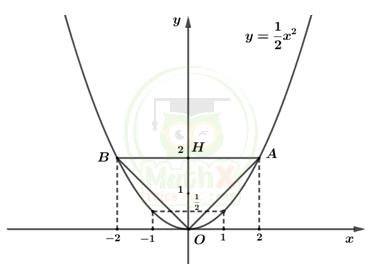
Theo giả thiết và dựa vào đồ thị hàm số \(y={\dfrac{1}{2}}x^2\) ta có: \(A\left(2;\ 2\right),B\left(-2;\ 2\right).\)
*) Viết phương trình đường thẳng AB
Giả sử phương trình đường thẳng AB có dạng y = ax + b
Vì đường thẳng AB đi qua điểm A (2 ; 2) nên 2 = 2a + b (1)
Vì đường thẳng AB đi qua điểm B (−2 ; 2) nên 2 = −2a + b (2)
Lấy (1) + (2) ta được: 2 + 2 \((2a+b)+(-2a+b)\Leftrightarrow4=2b\Leftrightarrow b=2\)
Với b = 2, thay vào (1), ta có: \(2=2a+2\Leftrightarrow a=0.\)
Vậy với a = 0 và b = 2 thì phương trình đường thẳng AB là y = 2
*) Chứng minh ΔOAB cân
Gọi AB ∩ Oy = {H}
Ta có: \(A H=B H=O H=|2|=2\)
Xét ΔOHA vuông tại H có: \(O B^{2}=B H^{2}+O H^{2}\) (định lý Py-ta-go)
Xét ΔOHA vuông tại H có: \(O A^{2}=A H^{2}+O H^{2}\) (định lý Py-ta-go)
Mà AH = BH nên OA = OB
=> ΔAOB cân tại O (đn)
Câu 2: 1) Giải hệ phương trình:
\(\left\{ \begin{array}{} x(x-3y) + y (y+x)=0 \\ {\sqrt{x}}.{\sqrt{y-2}}=1 \\ \end{array} \right.\)
2) Một hình chữ nhật có chu vi bằng 28m, diện tích bằng 48\(m^2\). Tìm các kích thước của hình chữ nhật đó.
Lời giải:
1) Điều kiện:
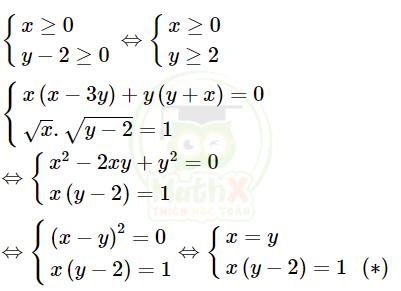
Thay x = y vào (*), ta có:
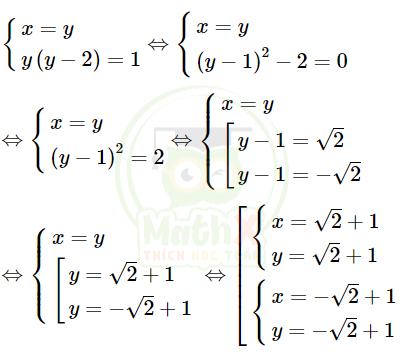
Vậy hệ phương trình có hai nghiệm là:
(x;y) ∈ \(\left\{\left({\sqrt{2}}+1;\ {\sqrt{2}}+1\right),\left(-{\sqrt{2}}+1;\ -{\sqrt{2}}+1\right)\right\}.\)
2) Gọi chiều rộng của hình chữ nhật là x (m, 0 < x < 7)
Nửa chu vi của hình chữ nhật là 28 : 2 = 14 (m)
Chiều dài của hình chữ nhật là 14 - x (m)
Vì chiều dài luôn lớn hơn chiều rộng => 14 - x > x <=> 2x < 14 <=> x < 7
Vì hình chữ nhật có diện tích bằng 48\(m^2\) nên ta có phương trình:
\(x\left(14-x\right)=48\)
\( \begin{array}{l} \Leftrightarrow - {x^2} - 14x - 48 = 0\\ \Leftrightarrow {x^2} - 14x + 48 = 0\\ \Leftrightarrow {x^2} - 6x - 8x + 48 = 0\\ \Leftrightarrow (x - 6)(x - 8) = 0 \end{array}\)
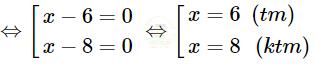
=> Chiều rộng của hình chữ nhật là 6 (m)
=> Chiều dài của hình chữ nhật là 14 - 6 = 8 (m)
Vậy chiều rộng của hình chữ nhật là 6m, chiều dài của hình chữ nhật là 8m
Câu 3: Cho hình chữ nhật ABCD(AB>AD nội tiếp đường tròn tâm O. Tia phân giác ∠ACD cắt cung nhỏ AD của đường tròn (O) tại điểm H
1) Chứng minh: Ba điểm A,O,C thẳng hàng và HA = HD
2) Dây HC của (O) cắt BD tại M, dây HB của (O) cắt AC tại N. Chứng minh: Tứ giác MNBC nội tiếp và MN⊥OH
3) Dây HB của (O) cắt AD tại I. Chứng minh IA < ID và AB . AC = BH
Lời giải:
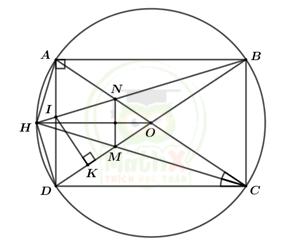
1) Chứng minh: Ba điểm A,O,C thẳng hàng và HA = HD
Vì hình chữ nhật ABCD nội tiếp đường tròn tâm O nên O là tâm của hình chữ nhật ABCD
Mà AC,BD là đường chéo của hình chữ nhật ABCD
=> O là trung điểm của đường chéo AC
=> Ba điểm A,O,C thẳng hàng.
Xét đườngtrong tâm O, ta có:
∠ACH = \(\dfrac{1}{2}sd\) cung AH (∠ACH là góc nội tiếp bị chắn bởi cung AH)
∠DCH = \(\dfrac{1}{2}sd\) cung DH (∠DCH là góc nội tiếp bị chắn bởi cung DH)
Mà ∠ACH = ∠DCH (giả thiết)
=> AH = DH (định lý liên hệ giữa cung và dây)
Hay HA = HD (đpcm)
2)
*) Chứng minh tứ giác MNBC nội tiếp
Xét đườngtrong tâm O, ta có:
∠ACH = \(\dfrac{1}{2}sd\) cung AH (∠ACH là góc nội tiếp bị chắn bởi cung AH)
∠DCH = \(\dfrac{1}{2}sd\) cung DH (∠DCH là góc nội tiếp bị chắn bởi cung DH)
Mà (chứng minh trên)
=> ∠ACH = ∠DCH hay Mà ∠NCM = ∠NBM
=> Tứ giác NBCM nội tiếp (Dấu hiệu nhận biết :tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh dưới hai góc bằng nhau)
*) Chứng minh MN ⊥ OH
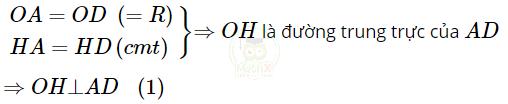
Xét tứ giác nội tiếp NBCM, ta có:
∠NMB = ∠NCB (góc nội tiếp bị chắn bởi cung NB)
Xét ΔOBC cân tại O (vì OB = OC = R) ta có:
∠OBC = ∠OCB (tính chất)
Hay ∠NCB = ∠MBC
=> ∠NMB = ∠MBC (= ∠NCB)
Mà ∠MBC và ∠NMB ở vị trí so le trong nên MN//BC (dấu hiệu nhận biết)
=> MN // AD (// BC) (2)
Từ (1) và (2) => MN ⊥ OH (quan hệ từ vuông góc đến song song)
3)
*) Chứng minh IA < ID
Kẻ IK ⊥ DB tại K
Xét ΔABI và ΔKBI ta có:
∠IAB = ∠IKB (\(=90^o\))
IB là cạnh chung
∠IAB = ∠IKB (góc nội tiếp bị chắn bởi hai cung bằng nhau HA và HD)
=> ΔABI = ΔKBI (cạnh huyền - góc nhọn)
=> IA = IK
Mà IK < ID (quan hệ giữa đường vuông góc và đường xiên trong ΔIKD vuông tại D)
=> IA < ID (đpcm)
*) Chứng minh AB.AC = BH.BI
Xét đường tròn (O) có ta có:
∠AHC \(=90^o\) (góc nội tiếp chắn nửa đường tròn)
=> BH = CH (liên hệ giữa cung và dây)
Xét ΔAIB và ΔHAC ta có:
∠IAB = ∠AHC (\(=90^o\))
∠IBA = ∠ACH (góc nội tiếp cùng chắn bởi cung AH)
=> ΔAIB ~ ΔHAC (g.g)
=> \({\dfrac{A B}{C H}}={\dfrac{B I}{A C}}\) (tỷ lệ cặp cạnh tương ứng)
=> AB.AC = CH.BI
Mà BH = CH (chứng minh trên)
=> AB.AC = BH.BI (đpcm)
Câu 4: Cho phương trình: \((x-1)\left(x^{2}+5m x+4m^{2}\right)=0\) (1) (với m là tham số). Tìm tất cả các giá trị của m để phương trình (1) có đúng hai nghiệm phân biệt.
Lời giải:
Xét phương trình (1):
\((x-1)\left(x^{2}+5m x+4m^{2}\right)=0\)
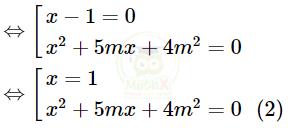
Để phương trình (1) có đúng hai nghiệm phân biệt thì phương trình (2) phải có nghiệm duy nhất và nghiệm đó khác 1.
Phương trình (2) có nghiệm duy nhất khi và chỉ khi:
Δ = \(b^{2}-4a c=0\)
\(\Leftrightarrow\left(5m\right)^{2}-4.1.4m^{2}=0\)
\(\Leftrightarrow9m^{2}=0\)
\(\Leftrightarrow m=0\)
Với m = 0 phương trình (2) trở thành: \(x^{2}=0\Leftrightarrow x={\stackrel{.}{0}}\ (x\neq1)\)
=> m = 0 (tm)
Vậy m = 0 thì phương trình \((x-1)\left(x^{2}+5m x+4m^{2}\right)=0\) có đúng 2 nghiệm phân biệt.
Trên đây MATHX đã hướng dẫn các em giải đề thi giữa kì 2 môn toán lớp 9 năm học 2023 - 2024 - đề 2. Ngoài ra các bậc phụ huynh cần cho con em mình học đúng phương pháp và tham khảo các khóa học online tại MATHX.VN để giúp con tự tin chinh phục môn toán nhé.
