
Thầy/cô MATHX.VN biên soạn tập hợp các số tự nhiên và các dạng toán về số tự nhiên - toán lớp 6 (phần 1). Tài liệu gồm lý thuyết trọng tâm, các dạng toán và bài tập chuyên đề tập hợp các số tự nhiên, cách ghi số tự nhiên .... và bài tập vận dụng online có đáp án và lời giải chi tiết, hỗ trợ các em học sinh trong quá trình học tập chương trình Toán 6 phần Số học chương 1: Ôn tập và bổ túc về số tự nhiên. Chúc các em học tốt!
1.1. Tập hợp, phần tử
Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định, những đối tượng đó được gọi là những phần tử của tập hợp mà ta nhắc đến.
Mối quan hệ giữa tập hợp và phần tử: Tập hợp chứa phần tử (nếu có) và phần tử nằm trong tập hợp.
Tập hợp là khái niệm cơ bản thường dùng trong toán học và cuộc sống. Ta hiểu tập hợp thông qua các ví dụ.
+ Ví dụ:
a) Tập hợp các bạn nữ trong lớp 6A bao gồm tất cả các bạn nữ của lớp 6A. Đối tượng của tập hợp này là các bạn nữ của lớp 6A. Mỗi một bạn là một phần tử.
b) Tập hợp các số nhỏ hơn gồm tất cả các số nhỏ hơn 6, đó là 0,1,2,3,4,5. Mỗi một số trong 6 số này là một phần tử của tập hợp, chẳng hạn số 0 là một phần tử, số 1 cũng là một phần tử.
+) Ta thường đặt tên cho tập hợp bằng các chữ cái in hoa: A, B, C, D,...
+) Sử dụng các chữ cái thường a,b,c,... để kí hiệu cho phần tử.
+) Các phần tử của tập hợp được viết trong dấu ngoặc nhọn { }, cách nhau bởi dấu phẩy “,” hoặc dấu “;” (đối với trường hợp là các phần tử số).
+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.
+) Phần tử x thuộc tập hợp A được kí hiệu là x ∈ A, đọc là “x thuộc A”. Phần tử y "không thuộc tập hợp A" được kí hiệu là y ∉ A, đọc là “y không thuộc A”.
Ví dụ: Tập hợp B gồm tất cả các số nhỏ hơn 5
Kí hiệu: B = {0; 1; 2; 3; 4}. Mỗi số 0; 1; 2; 3; 4 đều là một phần tử của tập hợp B. Số 6 không là phần tử của B (8 không thuộc B)
Ta viết 0 ∈ B; 1 ∈ B; 2 ∈ B
Ta không được viết
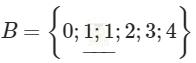
cách viết này có hai số 1 là cách viết sai.
- Các cách cho một tập hợp
Cách 1: Liệt kê các phần tử của tập hợp
Kí hiệu: B = {0; 1; 2; 3; 4}
Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó
Ngoài 2 cách cho tập hợp như trên, người ta còn minh họa bằng hình vẽ (Sơ đồ Venn).
vd:
a) Tập hợp B gồm tất cả các số nhỏ hơn 5
Liệt kê: B = {0; 1; 2; 3; 4}
Chỉ ra tính chất đặc trưng: B = {x | x < 5}
b) Tập hợp các số nhỏ hơn 6
Liệt kê: A = {0; 1; 2; 3; 4; 5}
Chỉ ra tính chất đặc trưng: B = {x | x < 6}
Sơ đồ Venn:
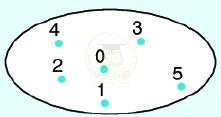
- Tập rỗng
Tập rỗng là tập hợp không có phần tử nào, kí hiệu ∅.
vd:
Giả sử lớp 6A là một lớp không có bạn nào trên 55kg. Nên tập hợp các bạn trên 55kg của lớp 6A là tập rỗng.
Các số 0,1,2,3,4,... là các số tự nhiên
Tập hợp các số tự nhiên được kí hiệu là N, tức là N = {0; 1; 2; 3;...}
Tập hợp các số tự nhiên khác 0 được kí hiệu là N∗, tức là N∗ = {1; 2; 3;...}
Tập hợp N bỏ đi số 0 thì được N*
Khi cho một số tự nhiên x ∈ N thì ta hiểu x là số tự nhiên khác 0.
Ví dụ:
Viết tập hợp sau bằng cách liệt kê các phần tử: A = {a ∈ N∗| a < 4}
a ∈ N∗ là các số từ 1; 2; 3; 4; 5; 6;...
Tuy nhiên thêm điều kiện a<4 nên a là các số 1; 2; 3.
Vậy A = {1; 2; 3}
Phương pháp:
Dùng một chữ cái in hoa và dấu ngoặc nhọn, ta có thể viết một tập hợp theo hai cách:
- Liệt kê các phần tử của nó.
- Chỉ ra tính chất đặc trưng cho các phần tử của nó
Phương pháp:
- Nắm vững ý nghĩa các kí hiệu ∈ và ∉
- Kí hiệu ∈ đọc là “phần tử của” hoặc “thuộc”.
- Kí hiệu ∉ đọc là “không phải là phần tử của” hoặc ‘không thuộc”.
Phương pháp:
Sử dụng biểu đồ ven. Đó là một đường cong khép kín, không tự cắt, mỗi phần tử của tập hợp được biểu diễn bởi một điểm ở bên trong đường cong đó.
- Cách ghi số tự nhiên trong hệ thập phân
Để ghi số tự nhiên trong hệ thập phân, người ta dùng mười chữ số là 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Người ta lấy các chữ số trong 10 chữ số này rồi viết liền nhau thành một dãy, vị trí của các chữ số đó trong dãy gọi là hàng.
Trong hệ thập phân, cứ 10 đơn vị của một hàng thì làm thành 1 đơn vị của hàng liền trước đó. Ví dụ 10 chục thì bằng 1 trăm; mười trăm thì bằng 1 nghìn;...
Chú ý: Khi viết các số tự nhiên, ta quy ước:
1. Với các số tự nhiên khác 0, chữ số đầu tiên bên trái khác 0.
2. Đối với các số có 4 chữ số khác 0 trở lên, ta viết tách riêng từng lớp. Mỗi lớp là một nhóm 3 chữ só từ phải sang trái.
3. Với những số tự nhiên có nhiều chữ số, mỗi chữ số ở các vị trí (hàng) khác nhau thì có giá trị khác nhau
Ví dụ:
Số 120 250 160 555
- Đọc: Một trăm hai mươi tỉ, hai trăm năm mươi triệu một trăm sáu mươi nghìn năm trăm năm mươi lăm.
- Các lớp: lớp tỉ, triệu, nghìn, đơn vị được ghi lại như sau:

Cùng là số 2 nhưng số 2 ở hàng chục tỉ có giá trị khác với số 2 ở hàng trăm triệu.
- Cấu tạo thập phân của một số
+ Kí hiệu \(\overline{{a b}}\) chỉ số tự nhiên có hai chữ số, chữ số hàng chục là a (a ≠ 0), chữ số hàng đơn vị là b.
Ta có:
\({\overline{{a b}}}=(a\times10)+b\) với a ≠ 0.
+ Kí hiệu \(\overline{{a bc}}\) chỉ số tự nhiên có 3 chữ số, chữ số hàng trăm là a, chữ số hàng chục là b, chữ số hàng đơn vị là c.
Ta có:
\({\overline{{a b c}}}=a.100+b.10+c\) với a ≠ 0.
+ Với các số tự nhiên cụ thể thì không có dấu gạch ngang trên đầu.
Ví dụ:
\({\overline{{2b}}}=2.10+b\)
\({\overline{{a5b}}}=a.100+5.10+b\,(a\not\neq0)\)
\(\overline{{{a03b c d}}}=a.100000+0.10000+3.100+c.10+d(a\neq0)\)
Cách viết số La Mã: Ta chỉ viết các số La Mã không quá 30.
+ Các thành phần để ghi số La Mã:
- Các kí tự I, V, X : Các chữ số La Mã.
- Các cụm chữ số IV, IX
- Giá trị của các thành phần này không thay đổi dù ở vị trí nào.

Các số La Mã biểu diễn các số từ 1 đến 10

Các số La Mã biểu diễn các số từ 11 đến 20: Thêm X vào bên trái mỗi số từ I đến X

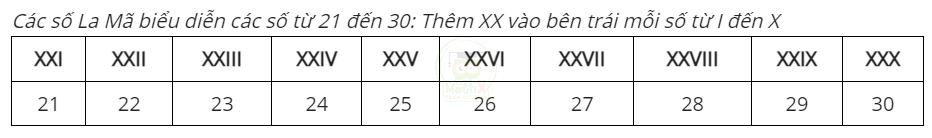
Chú ý:
- Mỗi số La Mã biểu diễn một số tự nhiên bằng tổng giá trị của các thành phần tạo nên số đó.
- Không có số La Mã nào biểu diễn số 0.
Ví dụ:
Số XIII có 4 thành phần là X, I, I, I tương ứng với các giá trị 10, 1, 1, 1. Do đó biểu diễn số 10 + 1 + 1 + 1 = 13.
Viết số 17 thành số La Mã:
Số 7 được viết là VII
Số 17 = 7 + 10, tức là số 7 thêm 10 đơn vị nên ta thêm chữ X trước VII được: XVII
Ngoài ra người ta còn sử dụng thêm một số thành phần khác:
|
Trong hệ La mã để ghi số tự nhiên người ta dùng bảy chữ số I; V; X; L; C; D; M có giá trị tương ứng trong hệ thập phân là 1; 5; 10; 50; 100; 500; 1000. Mỗi chữ số La Mã không viết liền nhau quá ba lần nên sáu số đặc biệt (trong các số này, chữ số có giá trị nhỏ đứng trước chữ số có giá trị lớn làm giảm giá trị của chữ số có giá trị lớn) là IV; IX; XL; XC; XD; XM (có giá trị trong hệ thập phân tương ứng là 4; 9; 40; 90; 400; 900) |
Phương pháp:
- Để tìm số liền sau của số tự nhiên a, ta tính a + 1.
- Để tìm số liền trước của số tự nhiên a khác 0,0,ta tính a − 1.
Chú ý:
- Số 0 không có số liền trước.
- Hai số tự nhiên liên tiếp thì hơn kém nhau 1 đơn vị.
Phương pháp:
Liệt kê tất cả các số tự nhiên thỏa mãn đồng thời các điều kiện đã cho
Ví dụ:
Tìm tất cả các số tự nhiên thỏa mãn 12 < x < 16
Giải:
Ta có: các số tự nhiên lớn hơn 12 và nhỏ hơn 16 là: 13; 14; 15
Phương pháp:
Giả sử từ ba chữ số a,b,c khác 0, ta viết các số có ba chữ số như sau:
Chọn a là chữ số hàng trăm ta có: \(\overline{abc}, \overline{acb};\)
Chọn b là chữ số hàng trăm ta có: \(\overline{bac}, \overline{bca};\)
Chọn c là chữ số hàng trăm ta có: \(\overline{cab}, \overline{cba};\)
Vậy tất cả có 6 số có ba chữ số lập được từ ba chữ số khác 0: a,b và c.
| Chữ số 0 không thể đứng ở hàng cao nhất của số có n chữ số phải viết. |
vd:
Dùng 2 chữ số 3, 5 hãy viết tất cả các số có 2 chữ số mà các chữ số khác nhau.
Giải:
Chữ số hàng chục có thể là 3 hoặc 5.
Nếu chữ số hàng chục là 3 thì chữ số hàng đơn vị là 5.
Nếu chữ số hàng chục là 5 thì chữ số hàng đơn vị là 3.
Phương pháp:
Bước 1: Tìm số nhỏ nhất và số lớn nhất có n chữ số.
Bước 2: Để tính số các chữ số có n chữ số ta lấy số lớn nhất có n chữ số trừ đi số nhỏ nhất có n chữ số rồi cộng với 1.
Ví dụ:
Có bao nhiêu số có 3 chữ số?
Giải:
Số lớn nhất có 3 chữ số là 999.
Số nhỏ nhất có 3 chữ số là: 100.
Số các số có 3 chữ số là 999 − 100 + 1 = 900
Phương pháp:
Để đếm các số tự nhiên từ a đến b, hai số liên tiếp cách nhau d đơn vị, ta dùng công thức sau:
\({\dfrac{b-a}{d}}+1\)
hay bằng (số cuối – số đầu) : khoảng cách + 1.
- Căn cứ vào các phần tử đã được liệt kê hoặc căn cứ vào tính chất đặc trưng cho các phần tử của tập hợp cho trước, ta có thể tìm được số phần tử của tập hợp đó.
- Sử dụng các công thức sau:
+ Tập hợp các số tự nhiên từ a đến b có: b − a + 1 phần tử (1)
+ Tập hợp các số chẵn từ số chẵn a đến số chẵn b có: (b − a) : 2 + 1 phần tử (2)
+ Tập hợp các số lẻ từ số lẻ m đến số lẻ n có: (n − m) : 2 + 1 phần tử (3)
+ Tập hợp các số tự nhiên từ a đến b, hai số kế tiếp cách nhau d đơn vị, có: (b − a) : d + 1 phần tử (4)
Phép cộng:
a + b = c
(số hạng) + (số hạng) = (tổng)
Minh họa trên tia số:
Phép cộng 3 + 2 = 5 : tổng hai tia bên trên bằng tia bên dưới.
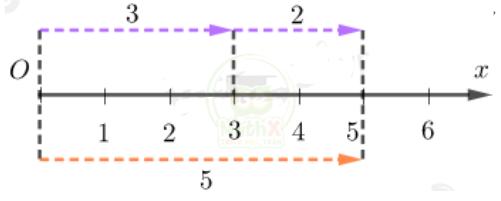
Tính chất:
Giao hoán: a + b = b + a
Kết hợp: (a + b) + c = a + (b + c) = a + b + c
a,b,c được gọi là tổng của ba số a,b,c
Cộng với số 0: a + 0 = 0 + a = a
Lưu ý: Khi cộng nhiều số, ta nên nhóm các số hạng có tổng là số chẵn tròn chục, tròn trăm,...(nếu có).
Ví dụ:
Tính một cách hợp lí: 12 + 25 + 15 + 28
Nhận xét: Ta thấy nếu tính riêng 12 + 28 và 25 + 15 thì được: 12 + 28 = 40 và 25 + 15 = 40 kết quả của hai phép tính này là tròn chục nên ta thực hiện phép tính sau:
12 + 25 + 15 + 28
= 12 + 28 + 25 + 15 (Đổi vị trí của các số 25, 15, 28: Tính chất giao hoán)
= (12 + 28) + (25 + 15) (Kết hợp)
= 40 + 40
= 80
Phép trừ
Cho hai số tự nhiên a và b, sao cho b + x = a thì ta có phép trừ
a − b = x
(số bị trừ) - (số trừ) = (hiệu)
|
Chú ý: Điều kiện để thực hiện được phép trừ là số bị trừ lớn hơn hoặc bằng số trừ. Nếu a − b = x thì a = b + x Nếu a + b = x thì a = x - b và b = x - a |
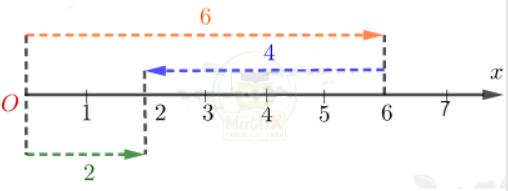
Minh họa trên tia số:
6 − 4 = 2
Số 6 biểu biễn bởi mũi tên từ trái sang phải
Số 4 biểu diễn mũi tên từ phải sang trái.
Phương pháp:
+ Để tìm số chưa biết trong một phép tính, ta cần nắm vững quan hệ giữa các số trong phép tính. Chẳng hạn: một số hạng bằng tổng của hai số trừ số hạng kia…
Ví dụ:
Tìm số tự nhiên x biết: x + 1 = 5
Giải:
x + 1 = 5
x = 5 − 1 = 5
x = 4
Phương pháp:
+ Muốn tìm một số hạng trong phép cộng hai số, ta lấy tổng trừ số hạng kia.
+ Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ.
+ Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu.
Phương pháp:
Áp dụng một số tính chất sau đây:
- Tổng của hai số không đổi nếu ta thêm vào ở số hạng này và bớt đi ở số hạng kia cùng một số đơn vị.
Ví dụ 1:
\(99+46=\left(99+1\right)+\left(46-1\right)=100+45=145.\)
- Hiệu của hai số không đổi nếu ta thêm vào một số bị trừ và số trừ cùng một số đơn vị.
Ví dụ 2:
\(315-97=(315+3)-(97+3)=318-100=218\)
Phương pháp:
Nhận xét, phát hiện và sử dụng các đặc điểm của các số hạng trong tổng. Từ đó dựa vào các tính chất của phép cộng để rút ra kết luận.
Ví dụ:
So sánh hai tổng 1367 + 5472 và 5377 + 1462 mà không tính giá trị cụ thể của chúng.
Giải:
Đặt A = 1367 + 5472 và B = 5377 + 1462
\(A=1367+5472\)
A = 1000 + 300 + 67 + 5000 + 400 + 62 + 10
A = 5000 + 1000 + 400 + 300 + 67 + 62 + 10
B = 5377 + 1462
B = 5000 + 300 + 67 + 10 + 1000 + 400 + 62
B = 5000 + 1000 + 400 + 300 + 67 + 62 + 10
Trên đây MATHX đã hướng dẫn các em ôn tập về tập hợp các số tự nhiên và các dạng toán về số tự nhiên - kèm bài tập vân dụng online Toán lớp 6 (phần 1). Ngoài ra các bậc phụ huynh cần cho con em mình học đúng phương pháp và tham khảo các khóa học online tại MATHX.VN để giúp con tự tin chinh phục môn toán nhé.
Các em tham khảo thêm phần 2 tại đây nhé:
CÁC DẠNG TOÁN VỀ SỐ TỰ NHIÊN - TOÁN LỚP 6 (PHẦN 2)