
Thầy/cô MATHX.VN biên soạn tập hợp các số tự nhiên và các dạng toán về số tự nhiên - Toán lớp 6 (phần 2). Tài liệu gồm lý thuyết trọng tâm, các dạng toán và bài tập chuyên đề tập hợp các số tự nhiên, cách ghi số tự nhiên .... và bài tập vận dụng online có đáp án và lời giải chi tiết, hỗ trợ các em học sinh trong quá trình học tập chương trình Toán 6 phần Số học chương 1: Ôn tập và bổ túc về số tự nhiên. Chúc các em học tốt!
1.1. Phép nhân số tự nhiên
Phép nhân số tự nhiên
Phép nhân hai số tự nhiên
(thừa số) . (thừa số) = (tích)
| Lưu ý: Nếu các thừa số đều bằng chữ, hoặc chỉ có một thừa số bằng số thì ta có thể không viết dấu nhân giữa các thừa số. Chẳng hạn, a x b = a . b = ab, 2 x a = 2 . a = 2a |
Ví dụ: Đặt tính nhân 254.45
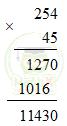
Giao hoán:
|
Chú ý: 1) Trong tính nhẩm ta thường sử dụng các kết quả: 2 . 5 = 10 4 . 25 = 100 8 . 125 = 1000 2) Tích |
Ví dụ: Tính nhẩm 12.25
(3 . 4) . 25 = 3 . (4 . 25) = 3 . 100 = 300
Chia hai số tự nhiên
Cho hai số tự nhiên
b . q + r trong đó r < b
Nếu 0
thì ta có phép chia hết:
(số bị chia) : (số chia) = (thương)
Nếu 0 thì ta có phép chia có dư. Ta nói
(số bị chia) = (số chia) . (thương) + (số dư)
Lưu ý: Số dư bao giờ cũng nhỏ hơn số chia.
Ví dụ: Thực hiện các phép chia sau
a) 445 : 13

Phương pháp:
+ Để tìm số chưa biết trong một phép tính, ta cần nắm vững quan hệ giữa các số trong phép tính. Chẳng hạn: thừa số bằng tích chia cho thừa số đã biết,…
+ Đặc biệt cần chú ý: với mọi a ∈ N ta đều có a . 0; a .1 = a
+ Nếu tích hai thừa số bằng 0 thì có ít nhất một thừa số bằng 0.
Ví dụ: Tìm x, biết x . 5 = 65
Giải:
x . 5 = 65
x = 65 : 5
x = 13
2.2
Phương pháp:
Dựa vào điều kiện xác định các chữ số trong số tự nhiên cần tìm để tìm từng chữ số có mặt trong số tự nhiên đó.
Ví dụ:
Tìm một số tự nhiên có hai chữ số, biết rằng khi thêm 21 vào bên trái số đó thì được một số mới gấp 31 lần số cần tìm.
Giải:
Gọi số cần tìm là \({\overline{{a b}}}.\) khi viết thêm số 21 vào bên trái số đó ta được số \({\overline{{21a b}}}.\)
Vì \({\overline{{21a b}}}.\) gấp 31 lần \({\overline{{a b}}}.\) nên ta có:
\({\overline{{a b}}}\times31={\overline{{21a b}}}\)
\(\overline{{{a b}}}\times31=2100+\overline{{{a b}}}\)
\({\overline{{a b}}}\times31-{\overline{{a b}}}\times1=2100\)
\({\overline{{a b}}}\times(31-1)=2100\)
\({\overline{{a b}}}\times30=2100\)
\({\overline{{a b}}}=2100:30\)
\({\overline{{a b}}} = 70\)
2.3. Áp dụng các tính chất của phép nhân để tính nhanh
Phương pháp:
- Quan sát, phát hiện các đặc điểm của các thừa số.
- Từ đó, xét xem nên áp dụng tính chất nào (giao hoán, kết hợp, phân phối) để tính một cách nhanh chóng.
Đặc biệt: Viết một số dưới dạng một tích để tính nhanh
Phương pháp:
Bước 1: Căn cứ theo yêu cầu của đề bài, ta có thể viết một số tự nhiên đã cho dưới dạng một tích của hai hay nhiều thừa số.
Bước 2: Sử dụng tính chất giao hoán, kết hợp và phân phối để tính một cách hợp lí.
Phương pháp:
Nhận xét, phát hiện và sử dụng các đặc điểm của các thừa số trong tổng hoặc tích. Từ đó dựa vào các tính chất phép nhân để rút ra kết luận.
Ví dụ:
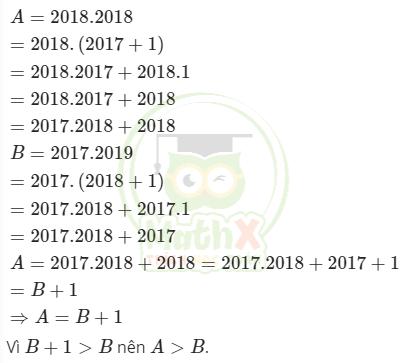
So sánh hai tích sau mà không tính giá trị của chúng
\(A=2018.2018;B=2017.2019\)
Giải:
Ta có:
Phương pháp:
Sử dụng định nghĩa của phép chia có dư và công thức:
\(a=b.q+r\left(0\lt r\lt b\right)\)
Từ công thức trên suy ra :
\(b={a}-r):q;q=(a-r):b;r=a-b.q.\)
Hay số bị chia = số chia x thương số + số dư
Số chia =(số bị chia – số dư) : thương số
Thương số = (số bị chia – số dư) : số chia
Số dư = số bị chia – số chia x thương số
Phương pháp:
+ Muốn tìm số bị chia ta, ta lấy thương nhân với số chia.
+ Muốn tìm số chia, ta lấy số bị chia chia cho thương.
Ví dụ:
Tìm số tự nhiên x biết:
a) 1236 : x = 12
b) x : 5 = 123
Giải:
a) 1236 : x = 12
x = 1236 : 12
x = 13
b) x : 5 = 123
x = 123 . 5
x = 615
Lũy thừa với số mũ tự nhiên
Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:
\(a^{n}=a. a\cdot\cdot\cdot a\) (n thừa số a) (n ∉ N*)
\(a^n\) đọc là “a mũ n” hoặc “a lũy thừa n”.
a được gọi là cơ số.
n được gọi là số mũ.
Phép nhân nhiều thừa số giống nhau như trên được gọi là phép nâng lên lũy thừa.
\(a^2 = a.a\) gọi là “a bình phương" (hay bình phương của a)
\(a^3 = a.a.a\)gọi là “a lập phương" (hay lập phương của a)
Với n là số tự nhiên khác 0 (thuộc N*) ta có:
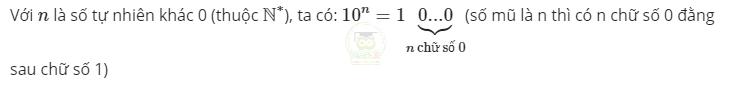
| Quy ước: \(a^{1}=a;a^{0}=1\left(a\neq0\right).\) |
Ví dụ:
a) \(8^3\) đọc là “tám mũ ba”, có cơ số là 8 và số mũ là 3.
b) Tính \(2^3\)
Số trên là lũy thừa bậc 3 của 2 và là tích của 3 thừa số 2 nhân với nhau nên ta có:
\(2^{3}=2.2.2=8\)
c) Tính \(10^3\)
\(10^3\) có số mũ là 3 nên \(10^{3}=1000\) (Sau chữ số 1 có 3 chữ số 0).
d) Viết 10 000 000 dưới dạng lũy thừa của 10:
Cách 1: \(1000000=10.10.10.10.10.10.10=10^{7}\)
Cách 2: Sau chữ số 1 có 7 chữ số 0 nên \(1000000=10^{7}\)
e) Viết 16 dưới dạng lũy thừa cơ số 4:
\(16=4.4=4^{2}\)
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.
\(a^{m}.a^{n}=a^{m+n}\)
Phép chia hai lũy thừa cùng cơ số
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ cho nhau.
\(a^{m}:a^{n}=a^{m-n}\,(a\neq0;\,m\geq n\geq0)\)
Ví dụ:
a) \(3^{5}:3=3^{5}:3^{1}=3^{5-1}=3^{4}=3.3.3.3=81\)
|
Lưu ý: Phép chia hai lũy thừa cùng cơ số không thể lấy hai số mũ chia cho nhau mà phải lấy hai số mũ trừ cho nhau. |
Phương pháp giải
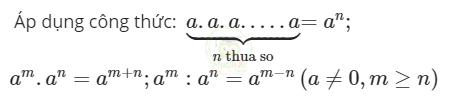
Phương pháp giải
Bước 1: Xác định cơ số và số mũ.
Bước 2: Áp dụng công thức:
Phương pháp giải
Để so sánh các số viết dưới dạng lũy thừa, ta có thể làm theo:
Cách 1: Đưa về cùng cơ số là số tự nhiên, rồi so sánh hai số mũ
Nếu m > n thì \(a^{m}\gt a^{n}\)
Cách 2: Đưa về cùng số mũ rồi so sánh hai cơ số
Nếu a > b thì \(a^{m}\gt b^{m}\)
Cách 3: Tính cụ thể rồi so sánh
Ngoài ra ta còn sử dụng tính chất bắc cầu: Nếu a < b; b < c thì a < c.
Phương pháp giải
Bước 1: Đưa về hai luỹ thừa của cùng một cơ số.
Bước 2: Sử dụng tính chất
Với a ≠ 0; a ≠ 1, nếu \(a^{m}= a^{n}\) thì m = n (a,m,n ∈ N)
Phương pháp giải
Cách 1: Dùng định nghĩa lũy thừa

- Đối với biểu thức không có dấu ngoặc
+ Nếu phép tính chỉ có cộng, trừ hoặc chỉ có nhân, chia, ta thực hiện phép tính theo thứ tự từ trái sang phải.
+ Nếu phép tính có cả cộng , trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân chia, cuối cùng đến cộng trừ.
Lũy thừa => nhân và chia => cộng và trừ.
- Đối với biểu thức có dấu ngoặc
Nếu biểu thức có các dấu ngoặc : ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính theo thứ tự: () => [] => {}

Phương pháp:
- Đối với biểu thức không có dấu ngoặc:
+ Nếu phép tính chỉ có cộng, trừ hoặc chỉ có nhân, chia, ta thực hiện phép tính theo thứ tự từ trái sang phải.
+ Nếu phép tính có cả cộng , trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân chia, cuối cùng đến cộng trừ.
Lũy thừa => nhân và chia => cộng và trừ
- Đối với biểu thức có dấu ngoặc.
Nếu biểu thức có các dấu ngoặc : ngoặc tròn ( ), ngoặc vuông [ ], ngoặc nhọn { }, ta thực hiện phép tính theo thứ tự: () => [] => {}
Phương pháp:
Để tìm số hạng chưa biết, ta cần xác định rõ xem số hạng đó nằm ở vị trí nào (số trừ, số bị trừ, hiệu, số chia,…). Từ đó xác định được cách biến đổi và tính toán.
Ví dụ:
Tìm số tự nhiên x, biết:
a) \(70-5.(x-3)=45\)
Ta coi 5(x - 3) làm một ẩn số cần tìm.
=> 5(x - 3) là số trừ trong phép trừ trên.
\(70-5.(x-3)=45\)
\(5.(x-3)=70-45\)
5.(x - 3) = 25
x - 3 = 25 : 5
x - 3 = 5
x = 5 + 3
x = 8
Phương pháp:
Tính riêng giá trị từng biểu thức rồi so sánh.
Ví dụ:
So sánh A và B biết:
\(A=125-2.[56-48:(15-7)]\) và \(B=75-25.10+25.13+180\)
Giải:
Ta có:

Trên đây MATHX đã hướng dẫn các em ôn tập về tập hợp các số tự nhiên và các dạng toán về số tự nhiên - kèm bài tập vân dụng online Toán lớp 6 (phần 2). Ngoài ra các bậc phụ huynh cần cho con em mình học đúng phương pháp và tham khảo các khóa học online tại MATHX.VN để giúp con tự tin chinh phục môn toán nhé.
Các em tham khảo thêm phần 1 tại đây nhé:
TẬP HỢP CÁC SỐ TỰ NHIÊN VÀ CÁC DẠNG TOÁN VỀ SỐ TỰ NHIÊN - TOÁN LỚP 6 (PHẦN 1)