GIẢI CHI TIẾT ĐỀ THI HỌC KÌ 1 TOÁN LỚP 9 PHÒNG GDĐT QUẬN HAI BÀ TRƯNG NĂM HỌC 2023 2024 - MATHX

 

Mathx.vn biên soạn gửi tới các em hướng dẫn giải chi tiết đề thi học kì 1 phòng gdđt quận hai bà trưng môn toán lớp 9 năm học 2023 2024. Các em học sinh tải để về làm trước sau đó so sánh kết quả và cách giải chi tiết trong bài viết này. Chúc các em học tập tốt!

 

 

 

 

 

ĐỀ THI HỌC KÌ 1 PHÒNG GDĐT QUẬN HAI BÀ TRƯNG

(ĐÁP ÁN + LỜI GIẢI CHI TIẾT)

Môn thi: Toán lớp 9

Năm học: 2023 - 2024

Thời gian làm bài: 90 phút

 

 

 

 

Bài 1 (1,0 điểm).

 

1. Thực hiện phép tính:

\({\sqrt{\left(1-{\sqrt{3}}\right)^{2}}}+{\sqrt{12}}-{\dfrac{6}{{\sqrt{3}}-1}}\,\)

 

 

2. Giải phương trình

\({\sqrt{x-1}}-{\dfrac{1}{2}}{\sqrt{4x-4}}+{\sqrt{{\dfrac{18x-18}{2}}}}=6\)

 

 

 

Giải

1)

Ta có:

\({\sqrt{\left(1-{\sqrt{3}}\right)^{2}}}+{\sqrt{12}}-{\dfrac{6}{{\sqrt{3}}-1}}\,\)

\(=\left|1-\sqrt{3}\right|+2\sqrt{3}-\dfrac{6\left(\sqrt{3}+1\right)}{3-1} \\ ={\sqrt{3}}-1+2{\sqrt{3}}-3\left({\sqrt{3}}+1\right) \\ =-4\)

 

 

2)

\({\sqrt{x-1}}-{\dfrac{1}{2}}{\sqrt{4x-4}}+{\sqrt{{\dfrac{18x-18}{2}}}}=6\)

\(\Leftrightarrow{\sqrt{x-1}}-{\dfrac{1}{2}}.2{\sqrt{x-1}}+3{\sqrt{x-1}}=6 \\ \Leftrightarrow3{\sqrt{x-1}}=6 \\ \Leftrightarrow{\sqrt{x-1}}=2 \\ \Leftrightarrow x = 5 \ (TM)\)

 

 

 

Bài 2 (2,0 điểm)

 

Cho biểu thức  \(A={\dfrac{{\sqrt{x}}+2}{{\sqrt{x}}+1}}\) và  \(B={\dfrac{4}{\sqrt{x}-2}}+{\dfrac{16}{4-x}}\) với \(x \geq 0\)  và \(x \neq 4\)

 

a) Tính giá trị biểu thức A khi x = 1.

b) Rút gọn biểu thức B.

c) Tìm các giá trị x là số chẵn để A.B > 1.

 

 

 

Giải

a)

Thay x = 1 (tmđk) vào biểu thức A

\(A={\dfrac{{\sqrt{1}}+2}{\sqrt{1+1}}} \\ A = \dfrac {3}{2}\)

 

 

b.

\(B={\dfrac{4}{\sqrt{x}-2}}+{\dfrac{16}{4-x}}\)

\(={\dfrac{4\left({\sqrt{x}}+2\right)}{\left({\sqrt{x}}-2\right)\left({\sqrt{x}}+2\right)}}-{\dfrac{16}{\left({\sqrt{x}}-2\right)\left({\sqrt{x}}+2\right)}} \\ ={\dfrac{4{\sqrt{x}}+8-16}{\left({\sqrt{x}}+2\right)\left({\sqrt{x}}-2\right)}} \\ ={\dfrac{4{\sqrt{x}}-8}{\left({\sqrt{x}}+2\right)\left({\sqrt{x}}-2\right)}} \\ ={\dfrac{4\left({\sqrt{x}}-2\right)}{\left({\sqrt{x}}+2\right)\left({\sqrt{x}}-2\right)}} \\ ={\dfrac{4}{\sqrt{x}+2}}\)

 

 

 

 

c)

\(A.B={\dfrac{\sqrt{x}+2}{\sqrt{x}+1}}\cdot{\dfrac{4}{\sqrt{x}+2}}={\dfrac{4}{\sqrt{x}+1}}\)

\(A.B\gt 1\Leftrightarrow{\dfrac{4}{\sqrt{x+1}}}\gt 1\Leftrightarrow{\dfrac{4}{\sqrt{x}+1}}-1\gt 0\)

\(\Leftrightarrow{\dfrac{3-{\sqrt{x}}}{\sqrt{x+1}}}\gt 0\)

 

Vì  \({\sqrt{x}}+1\gt 0\Rightarrow3{-}{\sqrt{x}}\gt 0\Rightarrow x\lt 9\) . Kết hợp điều kiện  \(x \geq 0\)  ; \(x \neq 4\) và x là số chẵn.

Vậy \(x\in\{0;2;6;8\}\)

 

 

 \((x^2y-3xy-x+3)=0 \Leftrightarrow (x-3)(xy-1) = 0 \Leftrightarrow \left[\begin{array}{c}{{x-3=0}}\\ {{xy-1=0}}\end{array}\right. \Leftrightarrow \left[\begin{array}{c}{{x=3}}\\ {{x=\dfrac{1}{y}}}\end{array}\right.\)

 

 

Bài 3 (3,0 điểm)

 

1) Giải phương trình sau bằng phương pháp thế: \(\begin{cases}{{x-2y=1}} \\ {{2x+y=7}} \end{cases}\)

 

 

2) Cho hàm số y = (m - 1)x + 3 (m là tham số, \(m \neq 1\)), có đồ thị là đường thẳng (d)

a) Vẽ đồ thị hàm số với m = 2

b) Tìm m để đường thẳng (d) song song với đường thẳng (d'): y = 2x - 1

c) Tìm điều kiện của m để (d) cắt trục Ox tại một điểm có hoành độ là số âm

 

 

Giải

1)

\(\begin{cases}{{x-2y=1}} \\ {{2x+y=7}} \end{cases} \Leftrightarrow \begin{cases}{{x=2y+1}} \\ {{2(2y+1)+y=7}} \end{cases} \\ \Leftrightarrow \begin{cases}{{x=2y+1}} \\ {{5y=5}} \end{cases} \\ \Leftrightarrow \begin{cases}{{x=2.1+1}} \\ {{y=1}} \end{cases} \\ \Leftrightarrow \begin{cases}{{x=3}} \\ {{y=1}} \end{cases}\)

 

Kết luận.

Lưu ý: học sinih sử dụng phương pháp cộng đại số trừ 0,25 điểm.

 

 

2)

a)

Thay m = 2 (TMĐK \(m \neq 1\) ) ta có hàm số:

y = x + 3

Lập bảng

x	0	-3
y = x + 3	3	0

 

Đồ thị hàm số là đường thẳng đii qua hai điểm (0;3) và (-3;0)

 

 

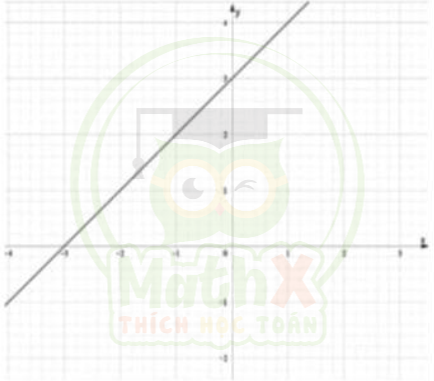
b)

(d) || (d') khi \(\begin{cases}{{m-1=2}} \\ {{3 \neq 1}} \end{cases}\)

\(\Leftrightarrow m = 3 \ (TMĐK)\)

Kết luận

 

c)

Gọi A là giao điểm của đồ thị hàm số và trục Ox. Tung độ A là y = 0

Thay vào hàm số:  \(0=\left(m-1\right)x+3\Rightarrow x={\dfrac{-3}{m-1}}\)  (do \(m \neq 1\))

Hoành độ A có giá trị âm khi  \({\dfrac{-3}{m-1}}\lt 0\Rightarrow m-1\gt 0\Rightarrow m\gt 1\)

 

 

 

Bài 4 (3,5 điểm)

 

1) Một gia đình làm cầu thang có độ dốc là \(36^o\) so với phương ngang. Chiều cao từ sàn đến trần nhà là 3,6m (hình bên dưới). Tính chiều dài AB của mặt cầu thang (làm tròn kết quả đến chữ số thập phân thứ nhất)

 

 

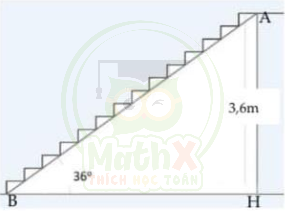
2) Cho tam giác ABC nhọn nội tiếp đường tròn (O) (AB < AC) . Vẽ đường cao AH của tam giác ABC và đường kính AD của đường tròn. AD cắt BC tại E, gọi K là chân đường vuông góc kẻ từ C tới AD.

a) Chứng minh bốn điểm A,H,K,C cùng thuộc một đường tròn

b) Gọi M là trung điểm của BC. Chứng minh \(\Delta E O M \) ~ \( {\Delta E C K}\)  và  \({\dfrac{M K}{O C}}={\dfrac{E M}{E O}}\)

c) Gọi I là trung điểm AC. Chứng minh IM đi qua trung điểm của HK.

 

 

 

Giải

1)

Xét \(\Delta ABH\) vuông tại H:

 \(sin B = \dfrac {AH}{AB}\)

Thay số:  \(\sin{36^{\circ}}={\dfrac{3,6}{A B}}\Rightarrow A B={\dfrac{3,6}{\sin{36^{\circ}}}}\approx6,1{\mathrm{m}}\)

 

 

2)

 

 

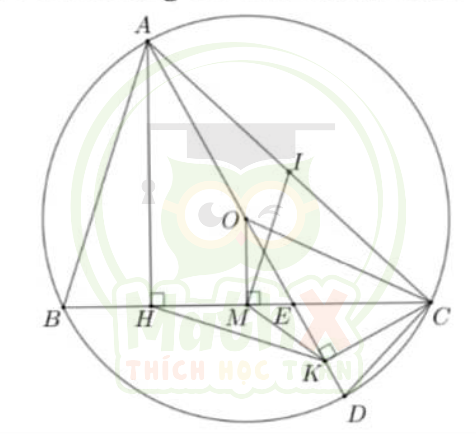
a)

Chứng minh được:

\(\Delta AHC\) vuông tại H; 3 điểm A, H, C thuộc đường tròn đường kính AC

\(\Delta AKC\) vuông tại H; 3 điểm A, K, C thuộc đường tròn đường kính AC

Từ đó kết luận 4 điểm A, H, K, C cùng thuộc một đường tròn

 

b)

* Chứng minh \(\Delta E O M \) ~ \( {\Delta E C K}\)

Do M là trung điểm BC và dây BC không đi qua tâm nên

\(O M\perp B C\Rightarrow {\widehat{OME}} =90^{\circ}\)

Xét  \(\Delta E O M \)  và  \( {\Delta E C K}\) có:

\( {\widehat{OME}} = {\widehat{EKC}} =90^{\circ}\)  ;  \({\widehat{OEM}} = {\widehat{KEC}}\) (đối đỉnh)

Vậy  \(\Delta E O M \) ~ \( {\Delta E C K}\)

 

* Chứng minh  \({\dfrac{M K}{O C}}={\dfrac{E M}{E O}}\)

 \(\Delta E O M \) ~ \( {\Delta E C K}\) 

\(\Rightarrow{\dfrac{E M}{E K}}={\dfrac{E O}{E C}}\Rightarrow{\dfrac{E M}{E O}}={\dfrac{E K}{E C}}\)

Xét  \(\Delta EMK \) và \(\Delta E O C\) có \({\dfrac{E M}{E O}}={\dfrac{E K}{E C}}\)  ;  \({\widehat{MEK}} = {\widehat{OEC}}\)  (đối đỉnh)

Vậy  \(\Delta E M K\) ~ \( {\Delta E O C}\)  (c.g.c)

\(\Rightarrow {\dfrac{M K}{O C}}={\dfrac{E M}{E O}}\)

 

 

c)

Do I là trung điểm AC và bốn điểm A, H, K, C cùng thuộc đường tròn đường kính AC nên IH = IK

Vậy I thuộc trung trực của HK

OM và AH cùng vuông góc với BC nên OM // AH

\(\Rightarrow {\dfrac{M H}{O A}}={\dfrac{E M}{E O}}\)  (Định lý Ta-lét)

Mặt khác \({\dfrac{E M}{E O}} = {\dfrac{M K}{O C}}\)  (đã chứng minh ở ý b)

Suy ra  \({\dfrac{MH}{OA}} = {\dfrac{M K}{O C}}\) 

Mà OA = OC nên MH = MK và M thuộc trung trực của HK

Vậy IM là trung trực của HK nên IM đi qua trung điểm của HK

 

 

 

Bài 5 (0,5 điểm)

 

Cho ba số thực dương a;b;c thỏa mãn: ab + bc + ca = 3

 

Tìm giá trị lớn nhất của: \(P={\dfrac{a}{\sqrt{3+a{{^2}}}}} + {\dfrac{b}{\sqrt{3+b{{^2}}}}} + {\dfrac{c}{\sqrt{3+c{{^2}}}}}\) 

 

 

 

Giải:

 

Ta có: 3 + \(a{^2}\) = \(a{^2}\) + ab + bc + ca = (a + b)(a + c)

 

Áp dụng BĐT Cauchy ta có:

 

\({\dfrac{a}{\sqrt{3+a{{^2}}}}}\) = \({\dfrac{a}{\sqrt{(a+b).(a+c)}}}\) = \(\sqrt {\dfrac{a}{{a + b}}×\dfrac{a}{{a + c}}} \le \dfrac{1}{2}\left( {\dfrac{a}{{a + b}} + \dfrac{a}{{a + c}}} \right)\)

 

Tương tự ta có: 

 

P \( \le \ \)\(\dfrac{1}{2}\) \(\begin{array}{l} \left( {\dfrac{a}{{a + b}} + \dfrac{a}{{a + c}} + \dfrac{b}{{b + a}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}} + \dfrac{c}{{c + b}}} \right) = \dfrac{3}{2}\\ \end{array} \)

 

Dấu "=" xảy ra khi và chỉ khi a = b = c.

 

Vậy giá trị lớn nhất của P = \(\dfrac{3}{2}\) khi a = b = c.

 

Trên đây MATHX đã hướng dẫn các em chữa đề thi học kì 1 phòng gdđt quận hai bà trưng môn toán lớp 9 năm học 2023 2024

Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong TÀI LIỆU TOÁN LỚP 9 để có thể tích lũy thêm nhiều kiến thức và ôn tập hiệu quả hơn.

 

Phụ huynh và các em học có thể tham khảo một số bài toán lớp 9 khác tại đây:

 

Bài toán về tập hợp và tính chia hết - đề hsg thcs cầu giấy 2023 2024

Một bài toán BĐT hay dùng phương pháp xét bất đẳng thức riêng