
MATHX gửi quý phụ huynh và các em học sinh một số câu hỏi hình học trong đề thi giữa kì I lớp 8 của các trường (bộ sách: Cánh diều) kèm đáp án chi tiết.
Câu 1. (Trường THCS Chu Văn An – Hà Nội)
Nhân dịp Trung thu, cô Lan cắt bìa làm thành các hộp quà để đựng kẹo tặng học sinh. Biết các hộp quà đều có dạng hình chóp tứ giác đều với cạnh 10 cm, trung đoạn có độ dài 12 cm và thể tích bằng 363,3 cm3.
a. Tính chiều cao của mỗi hộp quà (Kết quả làm tròn đến hàng phần mười)
b. Cô Lan muốn trang trí cho những chiếc hộp quà đó bằng cách dán giấy màu kín tất cả các mặt (kể cả mặt đáy). Hỏi nếu cô Lan có 1 m2 giấy màu thì có thể trang trí nhiều nhất bao nhiêu hộp quà? Giả sử các mép dán không đáng kể.
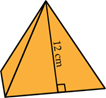
Hướng dẫn:
a) Mặt đáy của hộp quà là hình vuông có cạnh là \(10\,\text{cm}\).
Diện tích mặt đáy là \(S = 10 \cdot 10 = 100\,\text{cm}^2\).
Gọi chiều cao của hộp quà là \(h\) (cm).
Có \(V = \dfrac{1}{3} \cdot S \cdot h \Rightarrow h = \dfrac{3V}{S} = \dfrac{3 \cdot 363{,}3}{100} \approx 10{,}9\,(\text{cm})\).
Vậy chiều cao của hộp quà là \(10{,}9\,\text{cm}\).
b) Nửa chu vi đáy của hộp quà là: \(\dfrac{10 \cdot 4}{2} = 20\,(\text{cm})\).
Diện tích xung quanh của hộp quà là: \(20 \cdot 12 = 240\,(\text{cm}^2)\).
Diện tích toàn phần của hộp quà là: \(240 + 100 = 340\,(\text{cm}^2) = 0{,}034\,(\text{m}^2)\).
Với \(1\,\text{m}^2\) giấy màu, cô Lan có thể trang trí số hộp quà là: \(\dfrac{1}{0{,}034} \approx 29{,}41\,\text{hộp}\).
Vì cô Lan dán kín tất cả các mặt của hộp nên cô Lan dán nhiều nhất \(29\,\text{hộp}\).
Câu 2. (Trường THCS Thanh Am – Hà Nội)
Một con thuyền đang gặp sự cố gần bờ biển, thuyền viên đã sử dụng bộ đàm có bán kính hoạt động là 1km để gửi tín hiệu cấp cứu đến thiết bị thu tín hiệu trên đỉnh ngọn hải đăng gần đó (hình vẽ). Hỏi bộ đàm của thuyền viên có thể gửi tín hiệu đến thiết bị thu tín hiệu trên đỉnh ngọn hải đăng để cứu hộ không? Vì sao? (kết quả làm tròn đến hàng đơn vị)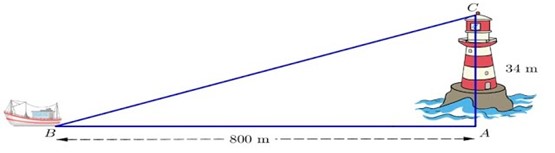
Hướng dẫn
Xét \( \triangle ABC \) có \( \widehat{BAC} = 90^{0} \)
\(\Rightarrow BC^{2} = AB^{2} + AC^{2}\) (Định lý Pythagore)
\(\Rightarrow BC = \sqrt{AB^{2} + AC^{2}} = \sqrt{800^{2} + 34^{2}} \approx 800{,}72\,(\text{m})\)
Mà \(800{,}72\,\text{m} < 1\,\text{km}\) nên bộ đàm của thuyền viên có thể gửi tín hiệu đến thiết bị thu tín hiệu trên đỉnh ngọn hải đăng để cứu hộ.
Câu 3. (Trường THCS Thanh Am – Hà Nội)
Để hưởng ứng cuộc thi “đồ dùng học tập tự làm”, bạn An đã làm một khối hình chóp tứ giác đều bằng gỗ cạnh đáy dài 6 dm, trung đoạn bằng 4 dm.
a) Tính diện tích xung quanh của khối gỗ?
b) Bạn An muốn sơn các mặt bên của khối gỗ. Cứ mỗi mét vuông sơn cần trả 100 000 đồng (tiền sơn và tiền công). Em hãy giúp bạn An tính chi phí phải trả?
Hướng dẫn:
a. Nửa chu vi đáy của khối là:\(\dfrac{1}{2}(6+6+6)=9\) (dm)
Diện tích xung quanh của khối gỗ là: 4.9 = 36 (dm2) = 0,36 (m2)
b. Chi phí mà bạn An phải trả là: 0,36.100 000 = 36 000 (đồng)
Vậy bạn An cần 36 000 đồng để sơn các mặt bên của gỗ.
Câu 4. (Trường THCS Đinh Tiên Hoàng – Khánh Hòa)
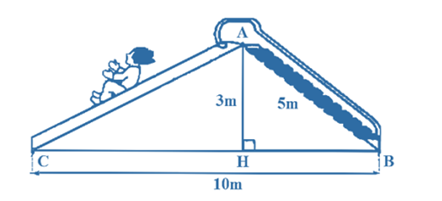
Một chiếc cầu trượt trong khu trò chơi có chiều cao AH = 3 m, chiều dài đường trượt AB = 5 m, khoảng cách giữa hai chân đường trượt BC = 10 m.
Hướng dẫn
a) Xét \( \triangle AHB \) có \( \widehat{BHA} = 90^{0} \)
\(\Rightarrow AB^{2} = AH^{2} + BH^{2}\) (Định lý Pythagore)
\(\Rightarrow BH = \sqrt{AB^{2} - AH^{2}} = \sqrt{5^{2} - 3^{2}} = \sqrt{16} = 4\,(\text{m})\)
b) Có \(CH = CB - BH = 10 - 4 = 6\,(\text{m})\)
Xét \( \triangle AHC \) có \( \widehat{AHC} = 90^{0} \)
\(\Rightarrow AC^{2} = AH^{2} + HC^{2}\) (Định lý Pythagore)
\(\Rightarrow AC = \sqrt{AH^{2} + HC^{2}} = \sqrt{6^{2} + 3^{2}} = \sqrt{45} \approx 6{,}71\,(\text{m})\)
Vậy \(BH = 4\,\text{m}; \quad AC \approx 6{,}71\,\text{m}\).
Câu 5. (Trường THCS Ngọc Lâm – Hà Nội)
1. Cho tam giác ABC vuông tại A, biết AB = 12 cm, BC = 13 cm. Tính độ dài AC.
2. Bánh ít lá gai là món bánh truyền thống của người dân Bình Định. Bánh thường xuất hiện trong các dịp quan trọng như: cưới hỏi, giỗ chạp, lễ hội thể hiện lòng thành kính và biết ơn tổ tiên. Vỏ bánh thường được làm bằng bìa có dạng hình chóp tứ giác đều cao 6 cm, cạnh đáy là 5 cm, độ dài trung đoạn là 6,5 cm
a) Tính thể tích một hộp bánh
b) Tính diện tích bìa cần dùng để làm 50 chiếc vỏ bánh như vậy (coi phần mép gấp không đáng kể)

1) Xét \( \triangle ABC \) có \( \widehat{BAC} = 90^{0} \)
\(\Rightarrow BC^{2} = AB^{2} + AC^{2}\) (Định lý Pythagore)
\(\Rightarrow AC = \sqrt{BC^{2} - AB^{2}} = \sqrt{13^{2} - 12^{2}} = \sqrt{25} = 5\,\text{cm}\)
Vậy \(AC = 5\,\text{cm}\).
2) a) Mặt đáy của hộp quà là hình vuông có cạnh là \(5\,\text{cm}\).
Diện tích mặt đáy là \(S = 5 \cdot 5 = 25\,\text{cm}^2\).
Chiều cao của hộp bánh là \(h = 6\,\text{cm}\).
Thể tích hộp bánh là \(V = \dfrac{1}{3} \cdot S \cdot h = \dfrac{1}{3} \cdot 25 \cdot 6 = 50\,(\text{cm}^3)\).
b) Nửa chu vi đáy của hộp bánh là \(\dfrac{5 \cdot 4}{2} = 10\,(\text{cm})\).
Diện tích xung quanh của hộp bánh là: \(S_{xq} = 10 \cdot 6{,}5 = 65\,(\text{cm}^2)\).
Diện tích toàn phần của hộp bánh là: \(S_{tp} = 65 + 25 = 90\,(\text{cm}^2)\).
Diện tích bìa cần dùng để làm 50 vỏ bánh là: \(90 \cdot 50 = 4500\,(\text{cm}^2)\).
Câu 6. (Trường THCS Thị Trấn Cái Rồng – Quảng Ninh)
Cho hình bình hành ABCD (\(AB > BC\)). Gọi E và K lần lượt là trung điểm của CD và AB; BD cắt AC tại O. Chứng minh rằng:
a) Tứ giác AECK là hình bình hành
b) Ba điểm E, O, K thẳng hàng.
Hướng dẫn:

a) Có ABCD là hình bình hành (gt)
\(\Rightarrow AB = CD; \; AB \parallel CD;\) O là trung điểm của AC và của BD.
Có K là trung điểm AB \(\Rightarrow AK = \dfrac{1}{2}AB\).
E là trung điểm của CD \(\Rightarrow EC = \dfrac{1}{2}CD\).
Mà \(AB = CD \Rightarrow AK = EC\).
Xét tứ giác AKCE có \(AK = EC;\; AK \parallel EC\).
\(\Rightarrow AECK\) là hình bình hành (Dấu hiệu nhận biết).
b) Gọi O' là giao của AC và EK.
Có AECK là hình bình hành \(\Rightarrow O'\) là trung điểm của AC và của EK.
Mà O là trung điểm của AC nên \(O \equiv O'\).
\(\Rightarrow O\) là trung điểm của \(EK\).
\(\Rightarrow E, O, K\) thẳng hàng.
Câu 7. (Trường THCS Đinh Tiên Hoàng – Khánh Hòa)
Cho tam giác ABC có \( AM \) là đường trung tuyến. Trên tia đối của tia MA lấy điểm D sao cho \( MD = MA \).
a) Chứng minh: Tứ giác ABDC là hình bình hành.
b) Kẻ đường cao AH của tam giác ABC. Gọi N là trung điểm của AC. Qua A kẻ đường thẳng song song với BC cắt tia HN tại E. Tứ giác AHCE là hình gì? Vì sao?
Hướng dẫn
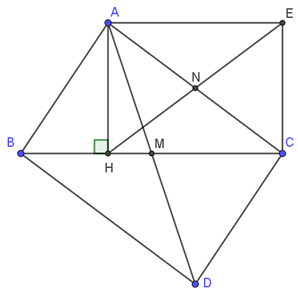
a) Xét tứ giác ABDC có
\( AM = MD = \dfrac{1}{2}AD \) (Vì AM là trung tuyến của \( \triangle ABC \))
\( BM = MC = \dfrac{1}{2}BC \)
\( \Rightarrow ABDC \) là hình bình hành (Dấu hiệu nhận biết)
b) Có \( AE \parallel HC \); \( \widehat{EAC} \) và \( \widehat{ACH} \) ở vị trí so le trong
\( \Rightarrow \widehat{EAC} = \widehat{ACH} \)
Xét \( \triangle EAN \) và \( \triangle HCN \) có:
\( \widehat{EAN} = \widehat{NCH} \)
\( AN = NC \)
\( \widehat{ANE} = \widehat{CNH} \) (hai góc đối đỉnh)
\( \Rightarrow \triangle EAN = \triangle HCN \) (g.c.g)
\( \Rightarrow AE = HC \) (hai cạnh tương ứng)
Xét tứ giác AECH có \( AE \parallel HC \), \( AE = HC \)
\( \Rightarrow AECH \) là hình bình hành (dấu hiệu nhận biết) mà \( \widehat{AHC} = 90^\circ \)
\( \Rightarrow AECH \) là hình chữ nhật (dấu hiệu nhận biết)
Câu 8. (Trường THCS & THPT Lương Thế Vinh – Hà Nội)
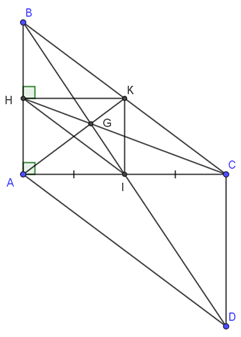
Cho tam giác ABC vuông tại A (\( AB < AC \)) có I là trung điểm của cạnh AC. Qua C, kẻ đường thẳng song song với đường thẳng AB, đường thẳng này cắt tia BI tại D.
a) Chứng minh \( \triangle ABI = \triangle CDI \) và suy ra tứ giác ABCD là hình bình hành.
b) Qua I kẻ đường thẳng IK \( \parallel AB \) (K ∈ BC). Gọi H là chân đường vuông góc hạ từ K xuống cạnh AB. Chứng minh \( AK = IH \).
c) Gọi G là giao điểm của AK và BD. Chứng minh ba điểm H, G, C thẳng hàng.
Hướng dẫn:
a) Có \( AB \parallel CD \) (gt); \( \widehat{BAC} \) và \( \widehat{ACD} \) ở vị trí so le trong
\( \Rightarrow \widehat{BAC} = \widehat{ACD} \)
Xét \( \triangle ABI \) và \( \triangle CDI \) có:
\( \widehat{AIB} = \widehat{CID} \) (hai góc đối đỉnh)
\( AI = IC \)
\( \widehat{BAC} = \widehat{ACD} \)
\( \Rightarrow \triangle ABI = \triangle CDI \) (g.c.g)
\( \Rightarrow BI = ID \) (hai cạnh tương ứng)
Xét tứ giác ABCD có \( AI = IC = \dfrac{1}{2}AC \); \( BI = ID = \dfrac{1}{2}BD \)
\( \Rightarrow ABCD \) là hình bình hành (Dấu hiệu nhận biết)
b) Có \( AB \perp AC \); \( IK \parallel AB \Rightarrow IK \perp AC \Rightarrow \widehat{AIK} = 90^\circ \)
Có \( HK \perp AB \Rightarrow \widehat{AHK} = 90^\circ \)
Xét tứ giác AHKI có \( \widehat{AHK} = \widehat{HKI} = \widehat{AIK} = 90^\circ \)
\( \Rightarrow AHKI \) là hình chữ nhật (dấu hiệu nhận biết)
\( \Rightarrow HI = AK \) (tính chất hình chữ nhật)
c) Có \( IK \perp AC \); \( AI = IC = \dfrac{1}{2}AC \)
\( \Rightarrow IK \) là đường trung trực của AC
\( \Rightarrow AK = KC \Rightarrow \triangle AKC \) cân tại K (định nghĩa)
\( \Rightarrow \widehat{KAC} = \widehat{KCA} \) (tính chất tam giác cân)
Có \( \widehat{ABC} + \widehat{BCA} = 90^\circ \) (Do \( \triangle ABC \) vuông tại A)
Lại có \( \widehat{BAK} + \widehat{KAC} = 90^\circ \); \( \widehat{BCA} = \widehat{KAC} \Rightarrow \widehat{ABC} = \widehat{BAK} \)
\( \Rightarrow \triangle BKA \) cân tại K (dấu hiệu nhận biết)
\( \Rightarrow BH = HA \) (Do \( HK \perp AB \) tại H); \( BK = AK \) mà \( AK = KC \Rightarrow BK = KC \)
\( \Rightarrow AK \) là trung tuyến của \( \triangle ABC \)
Mà BI cũng là trung tuyến của \( \triangle ABC \); \( AK \cap BI = \{G\} \)
\( \Rightarrow CG \) là trung tuyến của \( \triangle ABC \) mà H là trung điểm AB
\( \Rightarrow H, G, C \) thẳng hàng.
Câu 9. (Trường THCS Quảng Phú – Quảng Ngãi)
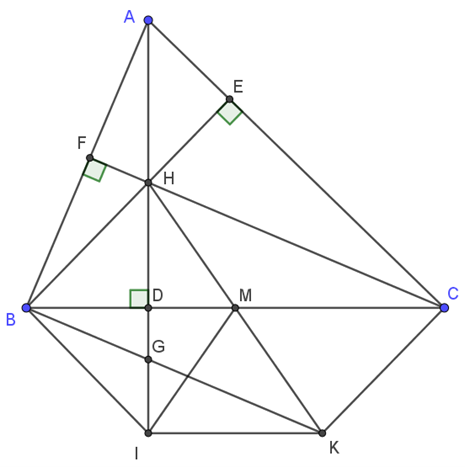
Cho tam giác ABC có 3 góc nhọn và \( AB < AC \). Các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC. Trên tia đối của MH lấy điểm K sao cho \( HM = MK \).
a) Chứng minh tứ giác BHCK là hình bình hành.
b) Chứng minh \( BK \perp AB \) và \( CK \perp AC \).
c) Gọi I là điểm sao cho BC là đường trung trực của đoạn thẳng HI. Chứng minh tứ giác BIKC là hình thang cân.
d) BK cắt HI tại G. Tam giác ABC phải có thêm điều kiện gì để tứ giác GHCK là hình thang cân.
Hướng dẫn:
a) Xét tứ giác BHCK có \( BM = MC = \dfrac{1}{2}BC \); \( HM = MK = \dfrac{1}{2}HK \) (gt)
\( \Rightarrow BHCK \) là hình bình hành (dấu hiệu nhận biết)
b) Có BHCK là hình bình hành
\( \Rightarrow HC \parallel BK;\; BH \parallel CK \) (tính chất hình bình hành)
Có \( BH \parallel CK;\; BH \perp AC \) (Vì BE là đường cao của \( \triangle ABC \)) \( \Rightarrow CK \perp AC \)
Có \( CH \parallel BK;\; CH \perp AB \) (Vì CF là đường cao của \( \triangle ABC \)) \( \Rightarrow BK \perp AB \)
c) Gọi D là giao của HI và BM
Có BM là trung trực của HI \( \Rightarrow BI = BH;\;\; HM = MI \) mà \( MK = HM \)
⇒ \( MH = MI = MK = \dfrac{1}{2}HK \)
Xét \( \triangle HIK \) có MI là đường trung tuyến; \( MI = \dfrac{1}{2}HK \)
⇒ \( \triangle HIK \) vuông tại I ⇒ \( \widehat{HIK} = 90^\circ \) ⇒ HI ⟂ IK mà HI ⟂ BC ⇒ BC // IK ⇒ BCKI là hình thang
Xét \( \triangle BHI \) có BH = BI ⇒ \( \triangle BHI \) cân tại B mà BD ⟂ HI
⇒ \( \widehat{HBD} = \widehat{IBD} \) mà \( \widehat{HBD} = \widehat{BCK} \) (do BH // CK)
⇒ \( \widehat{BCK} = \widehat{IBC} \)
Xét hình thang BCKI có \( \widehat{BCK} = \widehat{IBC} \)
⇒ BCKI là hình thang cân (dấu hiệu nhận biết)
d) Có H là trực tâm của \( \triangle ABC \) ⇒ AH ⟂ BC
Mà HD ⟂ BC ⇒ A, H, D thẳng hàng
Giả sử GHCK là hình thang cân
⇒ \( \widehat{GHC} = \widehat{HCK} \) mà \( \widehat{HCK} = \widehat{HBK} \) (do BHCK là hình bình hành)
⇒ \( \widehat{GHC} = \widehat{HBG} \) mà \( \widehat{GHC} = \widehat{AHF} \) (hai góc đối đỉnh)
\( \widehat{HBG} = \widehat{FHB} \) (do CH // BK)
⇒ \( \widehat{BHF} = \widehat{AHF} \) ⇒ HF là phân giác của \( \widehat{BHA} \); mà HF ⟂ AB
⇒ \( \triangle ABH \) cân tại H ⇒ AF = FB = \( \dfrac{1}{2}AB \) mà CF ⟂ AB
⇒ \( \triangle ABC \) cân tại C
Vậy \( \triangle ABC \) cân tại C thì HGCK là hình thang cân
Câu 10 (Trường THCS Ba Đình – Hà Nội)
Cho tam giác ABC vuông tại A (\( AB < AC, AC \ne 2AB \)), M là trung điểm của BC. Kẻ MH vuông góc với AC (\( H \in AC \)). Trên tia HM lấy điểm D sao cho \( HM = MD \).
a) Chứng minh: Tứ giác BHCD là hình bình hành.
b) Chứng minh: Tứ giác ABDH là hình chữ nhật.
c) Đường thẳng đi qua A song song với BC cắt đường thẳng đi qua C song song với AM tại K. Chứng minh AMCK là hình thoi.
d) Tam giác ABC cần có thêm điều kiện gì để tứ giác AMCK là hình vuông.
Hướng dẫn

a) Xét tứ giác BHCD có \( BM = MC = \dfrac{1}{2}BC \), \( MH = MD = \dfrac{1}{2}HD \)
⇒ BHCD là hình bình hành (dấu hiệu nhận biết).
b) Có BHCD là hình bình hành ⇒ \( BD \parallel AC \) mà \( DH \perp AC \Rightarrow DH \perp BD \Rightarrow \widehat{BDH} = 90^\circ \).
Có \( MH \perp AC \Rightarrow \widehat{DHA} = 90^\circ \).
Xét tứ giác ABDH có \( \widehat{BDH} = \widehat{DHA} = \widehat{HAB} = 90^\circ \)
⇒ ABDH là hình chữ nhật (dấu hiệu nhận biết).
c) Xét tứ giác AMCK có \( AM \parallel CK \); \( MC \parallel AK \)
⇒ AMCK là hình bình hành (dấu hiệu nhận biết)
Xét \( \triangle ABC \) có \( \widehat{BAC} = 90^\circ \); AM là đường trung tuyến của \( \triangle ABC \)
⇒ \( MA = MB = MC = \dfrac{1}{2}BC \)
Xét hình bình hành AMCK có \( MA = MC \)
⇒ AMCK là hình thoi (dấu hiệu nhận biết)
d) Giả sử AMCK là hình vuông
⇒ \( \widehat{AMC} = 90^\circ \Rightarrow AM \perp BC \)
Xét \( \triangle ABC \) có AM là đường cao, AM là đường trung tuyến của tam giác
⇒ \( \triangle ABC \) cân tại A (dấu hiệu nhận biết) mà \( \widehat{BAC} = 90^\circ \)
⇒ \( \triangle ABC \) vuông cân tại A
Vậy cần thêm điều kiện là tam giác ABC vuông cân tại A để AMCK là hình vuông.
GIỚI THIỆU LỚP HỌC ONLINE CÙNG GIÁO VIÊN GIỎI
Trường Toán Online MATHX với các lớp Toán online trực tiếp với giáo viên giỏi.
Lớp học dành cho học sinh từ CƠ BẢN đến NÂNG CAO phù hợp với trình độ của từng bạn (có kiểm tra xếp lớp).
Sĩ số 8 - 12 học sinh/lớp giúp giáo viên và học sinh dễ dàng tương tác, giáo viên dễ dàng sát sao tình hình học tập của học sinh.
Phụ huynh học sinh đăng ký LÀM BÀI KIỂM TRA XẾP LỚP MIỄN PHÍ tại form:
truongtoanmathx.vn/dangkykiemtra
Xem thông tin chi tiết: truongtoanmathx.vn
HOTLINE: 0867.162.019