CÁC KHÁI NIỆM CƠ BẢN VỀ PHÂN SỐ VÀ BÀI TẬP VẬN DỤNG ONLINE - TOÁN LỚP 4

 

Trong bài học này thầy/cô MATHX chia sẻ đến các em học sinh các khái niệm cơ bản về phân số: phân số bằng nhau, rút gọn phân số, phân số và phép chia số tự nhiên, quy đồng mẫu số và so sánh hai phân số (cơ bản đến nâng cao) kèm một số bài tập vận dụng online. Các em ôn tập lý thuyết và trả lời câu hỏi vận dụng online để đối chiếu kết quả. Chúc các em học tốt!

 

Quý phụ huynh và các em học sinh xem thêm một số bài viết về kiến thức lớp 4 tại đây:

 

TOÁN NÂNG CAO LỚP 4 - MỘT SỐ BÀI TẬP VỀ DÃY SỐ

TOÁN NÂNG CAO LỚP 4 - BÀI TOÁN TRỒNG CÂY

 

 

 

I. Kiến thức cần nhớ

 

 

 

1. PHÂN SỐ

Mẫu số là số tự nhiên viết dưới gạch ngang. Mẫu số cho biết hình tròn được chia thành 6 phần bằng nhau.

Tử số là số tự nhiên viết trên gạch ngang. Tử số cho biết 5 phần bằng nhau đã được tô màu.

 

1.1. Cách đọc, viết phân số

Ví dụ: Phân số chỉ phần đã tô màu trong mỗi hình dưới đây được viết, đọc như sau:

 

1.2. Nhận xét

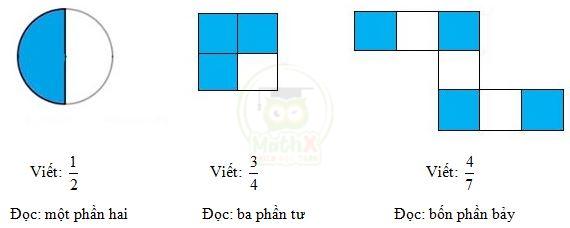
\({\cfrac{5}{6}}\ ;\ {\cfrac{1}{2}}\ ;\ \ {\cfrac{3}{4}}\ ;\ \ {\cfrac{4}{7}}\) là những phân số.

Mỗi phân số có tử số và mẫu số. Tử số là số tự nhiên viết trên gạch ngang. Mẫu số là số tự nhiên khác 0 viết dưới gạch ngang.

 

 

 

2. PHÂN SỐ VÀ PHÉP CHIA SỐ TỰ NHIÊN

a) Có 8 quả cam, chia đều cho 4 Mỗi em được:

8 : 4 = 2 (quả cam)

b) Có 3 cái bánh, chia đều cho 4 Hỏi mỗi em được bao nhiêu phần của cái bánh?

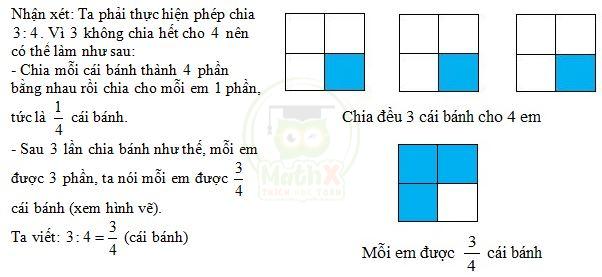
c) Nhận xét:

Thương của phép chia số tự nhiên cho số tư nhiên (khác 0) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia.

Chẳng hạn:

\(8:4={\dfrac{8}{4}}\quad;\quad3:4={\dfrac{3}{4}}\quad;\quad5:5={\dfrac{5}{5}}\ .\)

 

2.1 Phân số lớn hơn 11, bằng 11, nhỏ hơn 11 

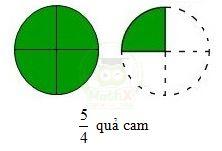
a) Ví dụ 1: Có 2 quả cam, chia mỗi quả cam thành 4 phần bằng nhau. Vân ăn 1 quả cam và \(\dfrac{1}{4}\) quả cam. Viết phân số chỉ số phần quả cam Vân đã ăn.

Ta thấy: Ăn 1 quả cam, tức là ăn 4 phần hay \(\dfrac{4}{4}\) quả cam; ăn thêm \(\dfrac{1}{4}\) quả cam nữa, tức là ăn thêm 1 phần, như vậy Vân đã ăn tất cả 5 phần hay \(\dfrac{5}{4}\) quả cam.

b) Ví dụ 2: Chia đều 5 quả cam cho 4 người. Tìm phần cam của mỗi người.

Ta có thể làm như sau: Chia mỗi quả cam thành 4 phần bằng nhau. Lần lượt đưa cho mỗi người 1 phần, tức là \(\dfrac{1}{4}\) của từng quả cam. Sau 5 lần chia như thế, mỗi người được 5 phần hay \(\dfrac{5}{4}\) quả cam.

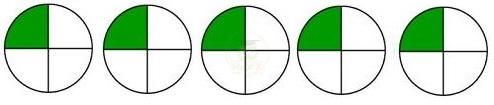
Vậy: \(5:4={\dfrac{5}{4}}\) (quả cam)

c) Nhận xét:

- Kết quả của phép chia số tự nhiên cho số tự nhiên (khác 0) có thế viết là một phân số, chẳng hạn:

\(5:4={\dfrac{5}{4}}\).

 

 

3. PHÂN SỐ BẰNG NHAU. RÚT GỌN PHÂN SỐ

3.1  Phân số bằng nhau

a) Có hai băng giấy bằng nhau.

b) Nhận xét: \({\dfrac{3}{4}}={\dfrac{3\times2}{4\times2}}={\dfrac{6}{8}}\operatorname \ {và}\qquad{\dfrac{6}{8}}={\dfrac{6:2}{8:2}}={\dfrac{3}{4}}.\)

Từ nhận xét này, có thể nêu tính chất cơ bản của phân số như sau:

Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho. Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác 0 thì sau khi chia ta được một phân số bằng phân số đã cho.

 

3.2 Rút gọn phân số

Có thể rút gọn phân số để được một phân số có tử số và mẫu số bé đi mà phân số mới vẫn bằng phân số đã cho.

Ví dụ 1: Rút gọn phân số: \(\dfrac{6}{8}\)

Ta thấy: 6 và 8 đều chia hết cho 2 nên \({\dfrac{6}{8}}={\dfrac{6:2}{8:2}}={\dfrac{3}{4}}.\)

3 và 4 không cùng chia hết cho một số tự nhiên nào lớn hơn 1, nên phân số \(\dfrac{3}{4}\) không thể rút gọn được nữa. Ta nói rằng: \(\dfrac{3}{4}\) là phân số tối giản và phân số \(\dfrac{6}{8}\) đã được rút gọn thành phân số tối giản \(\dfrac{3}{4}\).

Ví dụ 2: Rút gọn phân số: \(\dfrac{18}{54}\)

Ta thấy: 18 và 54 đều chia hết cho 2 nên

\({\dfrac{18}{54}}={\dfrac{18:2}{54:2}}={\dfrac{9}{27}}\)

9 và 27 cùng chia hết cho 9 nên

\({\dfrac{9}{27}}={\dfrac{9:9}{27:9}}={\dfrac{1}{3}}\)

1 và 3 không cùng chia hết cho một số tự nhiên nào lớn hơn 1, nên \(\dfrac{1}{3}\) là phân số tối giản.

Vậy \({\dfrac{18}{54}}={\dfrac{1}{3}}\)

Khi rút gọn phân số có thể làm như sau: - Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 11. - Chia tử số và mẫu số cho số đó. Cứ làm như thế cho đến khi nhận được phân số tối giản.

Lưu ý: Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn 1, hay phân số tối giản là phân số không thể rút gọn được nữa.

 

 

 

 

4. QUY ĐỒNG MẪU SỐ CÁC PHÂN SỐ

4.1. Cách quy đồng mẫu số các phân số:

a) Khi quy đồng mẫu số hai phân số có thể làm như sau:

- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.

- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.

b) Nếu mẫu số của phân số thứ hai mà chia hết cho mẫu số của phân số thứ nhất thì ta có thể quy đồng mẫu số hai phân số như sau:

- Lấy mẫu số chung là mẫu số của phân số thứ hai.

- Tìm thừa số phụ bằng cách lấy mẫu số thứ hai cho cho mẫu số thứ nhất.

- Nhân cả tử số và mẫu số của phân số thứ nhất với thừa số phụ tương ứng.

- Giữ nguyên phân số thứ hai.

Chú ý: ta thường lấy mẫu số chung là số tự nhiên nhỏ nhất khác 00 và cùng chia hết cho tất cả các mẫu.

4.2. Ví dụ

Ví dụ 1: Quy đồng mẫu số hai phân số \(\dfrac{1}{3}\) và \(\dfrac{2}{5}\)

Chọn mẫu số chung (MSC) là 3 × 5 = 15.

Quy đồng mẫu số hai phân số ta có:

\({\dfrac{1}{3}}={\dfrac{1\times5}{3\times5}}={\dfrac{5}{15}}~;~~~~~~~~~~~~~~{\dfrac{2}{5}}=~{\dfrac{2\times3}{5\times3}}={\dfrac{6}{15}}\)

Vậy quy đồng mẫu số hai phân số \(\dfrac{1}{3}\) và \(\dfrac{2}{5}\) ta được hai phân số \(\dfrac{5}{15}\) và \(\dfrac{6}{15}\) 

Ví dụ 2: Quy đồng mẫu số hai phân số \(\dfrac{7}{6}\) và \(\dfrac{5}{12}\)

Ta thấy mẫu số của phân số \(\dfrac{5}{12}\) chia hết cho mẫu số của phân số \(\dfrac{7}{6}\) (12 : 6 = 2).

Chọn mẫu số chung là 12.

Ta có thể quy đồng đồng mẫu số hai phân số \(\dfrac{7}{6}\) và \(\dfrac{5}{12}\) như sau:

\({\dfrac{7}{6}}={\dfrac{7\times2}{6\times2}}={\dfrac{14}{12}}\) và giữ nguyên phân số \(\dfrac{5}{12}\).

Vậy quy đồng đồng mẫu số hai phân số \(\dfrac{7}{6}\) và \(\dfrac{5}{12}\) được hai phân số \(\dfrac{14}{12}\) và \(\dfrac{5}{12}\) 

 

 

 

5. SO SÁNH HAI PHÂN SỐ (CƠ BẢN)

5.1. So sánh các phân số cùng mẫu số

Quy tắc: Trong hai phân số có cùng mẫu số:

+) Phân số nào có tử số bé hơn thì phân số đó bé hơn.

+) Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.

+) Nếu tử số bằng nhau thì hai phân số đó bằng nhau.

Ví dụ: \({\dfrac{3}{8}}\lt {\dfrac{5}{8}};\qquad{\dfrac{5}{8}}\gt {\dfrac{3}{8}};\qquad{\dfrac{7}{8}}={\dfrac{7}{8}}.\)

 

4.2. So sánh các phân số cùng tử số

Quy tắc: Trong hai phân số có cùng tử số:

+) Phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.

+) Phân số nào có mẫu số lớn hơn thì phân số đó bé hơn.

+) Nếu mẫu số bằng nhau thì hai phân số đó bằng nhau.

Ví dụ: \({\dfrac{1}{2}}\gt {\dfrac{1}{4}};\qquad{\dfrac{2}{7}}\lt {\dfrac{2}{5}};\qquad{\dfrac{5}{6}}={\dfrac{5}{6}}.\)

Chú ý: Phần so sánh các phân số cùng tử số, học sinh rất hay bị nhầm, các bạn HS nên chú ý nhớ và hiểu đúng quy tắc.

 

5.3. So sánh các phân số khác mẫu

a) Quy đồng mẫu số

Quy tắc: Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó rồi so sánh các tử số của hai phân số mới.

Phương pháp giải:

Bước 1: Quy đồng mẫu số hai phân số.

Bước 2: So sánh hai phân số có cùng mẫu số đó.

Bước 3: Rút ra kết luận.

Ví dụ: So sánh hai phân số: \(\dfrac{2}{3}\) và \(\dfrac{5}{7}\) 

Cách giải:

Ta có: MSC = 21. Quy đồng mẫu số hai phân số ta có

\({\dfrac{2}{3}}={\dfrac{2\times7}{3\times7}}={\dfrac{14}{21}};\qquad\qquad{\dfrac{5}{7}}={\dfrac{5\times3}{7\times3}}={\dfrac{15}{21}}\)

Vậy \({\dfrac{2}{3}}\lt {\dfrac{5}{7}}.\)

b) Quy đồng tử số

Điều kiện áp dụng: Khi hai phân số có mẫu số khác nhau nhưng mẫu số rất lớn và tử số nhỏ thì ta nên áp dụng cách quy đồng tử số để việc tính toán trở nên dễ dàng hơn.

Quy tắc: Muốn so sánh hai phân số khác tử số, ta có thể quy đồng tử số hai phân số đó rồi so sánh các mẫu số của hai phân số mới.

Phương pháp giải:

Bước 1: Quy đồng tử số hai phân số.

Bước 2: So sánh hai phân số có cùng tử số đó.

Bước 3: Rút ra kết luận.

Ví dụ: So sánh hai phân số: \(\dfrac{2}{123}\) và \(\dfrac{3}{185}\) 

Cách giải:

Ta có: TSC = 6. Quy đồng tử số hai phân số ta có:

\({\dfrac{2}{123}}={\dfrac{2\times3}{123\times3}}={\dfrac{6}{369}};\qquad\qquad{\dfrac{3}{185}}={\dfrac{3\times2}{185\times2}}={\dfrac{6}{370}}\)

Ta thấy hai phân số \(\dfrac{6}{369}\) và \(\dfrac{6}{370}\) đều có tử số là 6 và 369 < 370 nên \({\dfrac{6}{369}}\gt {\dfrac{6}{370}}\)

 Vậy \({\dfrac{2}{123}}\gt {\dfrac{3}{185}}\)

 

 

 

 

 

6. SO SÁNH HAI PHÂN SỐ (NÂNG CAO)

6.1. Một số cách so sánh khác

Dạng 1: So sánh với 1

Điều kiện áp dụng:  Phương pháp này áp dụng cho dạng bài so sánh hai phân số, trong đó một phân số bé hơn 1 và một phân số lớn hơn 1.

Ví dụ: So sánh hai phân số  \(\dfrac{5}{9}\) và \(\dfrac{8}{7}\) 

Cách giải:

Ta thấy \(\textstyle{\dfrac{5}{9}}\lt 1\) và  1 < \(\dfrac{8}{7}\) nên \({\dfrac{5}{9}}\lt {\dfrac{8}{7}}\)

Dạng 2: So sánh với phân số trung gian

Điều kiện áp dụng: Phương pháp này áp dụng khi tử số của phân số thứ nhất bé hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại lớn hơn mẫu số của phân số thứ hai hoặc ngược lại. Khi đó ta so sánh với phân số trung gian là phân số có tử số bằng tử số của phân số thứ nhất và mẫu số bằng mẫu số của phân số thứ hai hoặc ngược lại, phân số trung gian là phân số có tử số bằng tử số của phân số thứ hai và mẫu số bằng mẫu số của phân số thứ nhất.

Phương pháp giải:

Bước 1: Chọn phân số trung gian.

Bước 2: So sánh hai phân số ban đầu với phân số trung gian.

Bước 3: Rút ra kết luận.

Lưu ý: So sánh hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) (a,b,c,d khác 0)

Nếu a > c và b < d (hoặc a < c và b > d)  thì ta có thể chọn phân số trung gian là \(\dfrac{a}{d}\) hoặc \(\dfrac{c}{b}\)

Ví dụ: So sánh hai phân số \(\dfrac{27}{49}\) và \(\dfrac{28}{39}\) 

Cách giải: 

Chọn phân số trung gian là \(\dfrac{27}{49}\)

Ta thấy \({\dfrac{27}{49}}\lt {\dfrac{27}{39}}\) và \({\dfrac{27}{39}}\lt {\dfrac{28}{39}}\) nên \({\dfrac{27}{49}}\lt {\dfrac{28}{39}}\)

 

Dạng 3: So sánh bằng phần bù 

Điều kiện áp dụng: Nhận thấy mẫu số lớn hơn tử số ( phân số bé hơn 1) và hiệu của mẫu số với tử số của tất cả các phân số đều bằng nhau hoặc nhỏ thì ta tìm phần bù với 1.

Chú ý: Phần bù của một phân số là phân số có tử số bằng hiệu của mẫu số và tử số của phân số ban đầu và giữ nguyên mẫu số.

Quy tắc: Trong hai phân số, phân số nào có phần bù lớn hơn thì phân số đó nhỏ hơn và ngược lại phân số nào có phần bù nhỏ hơn thì phân số đó lớn hơn.

Phương pháp giải:

Bước 1: Tìm phần bù của hai phân số.

Bước 2: So sánh hai phần bù với nhau.

Bước 3: Rút ra kết luận.

Ví dụ: So sánh hai phân số \(\dfrac{456}{457}\) và \(\dfrac{458}{459}\) 

Cách giải: 

Phần bù của \(\dfrac{456}{457}\) là \(\dfrac{1}{457}\)

Phần bù của \(\dfrac{458}{459}\) là \(\dfrac{1}{459}\)

Vì 457 < 459 nên \({\dfrac{1}{457}}\gt {\dfrac{1}{459}}\)

Do đó: \({\dfrac{456}{457}}\lt {\dfrac{458}{459}}\)

 

Dạng 4: So sánh bằng phần hơn

Điều kiện áp dụng: Nhận thấy tử số lớn hơn mẫu số ( phân số lớn hơn 1) và hiệu của tử số với mẫu số của tất cả các phân số đều bằng nhau hoặc nhỏ thì ta tìm phần hơn với 11.

Chú ý: Phần hơn của một phân số là phân số có tử số bằng hiệu của tử số và mẫu số của phân số ban đầu và giữ nguyên mẫu số.

Quy tắc: Trong hai phân số, phân số nào có phần hơn lớn hơn thì phân số đó lớn hơn và ngược lại phân số nào có phần hơn nhỏ hơn thì phân số đó nhỏ hơn.

Phương pháp giải:

Bước 1: Tìm phần hơn của hai phân số.

Bước 2: So sánh hai phần hơn với nhau

Bước 3: Rút ra kết luận.

Ví dụ: So sánh hai phân số \(\dfrac{999}{997}\) và \(\dfrac{579}{577}\) 

Cách giải:

Phần hơn của \(\dfrac{999}{997}\) là \(\dfrac{2}{997}\)

Phần hơn của \(\dfrac{579}{577}\) là \(\dfrac{2}{577}\)

Vì 997 > 577 nên \({\dfrac{2}{997}}\lt {\dfrac{2}{577}}\)

Do đó \(\dfrac{999}{997}\lt \dfrac{579}{577}.\)

 

 

 

II. Bài tập vận dụng online

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Trên đây là các khái niệm cơ bản về phân số và bài tập dụng online toán lớp 4. Tuy đây chỉ là các kiến thức cơ bản nhưng lại là nền móng vô cùng quan trọng để học những kiến thức sâu hơn. Các bậc phụ huynh cần cho con em mình học đúng phương pháp để đạt tích lũy được đủ kiến thức tránh để con học mất gốc.

 

Tham khảo thêm nội dung kiến thức toán lớp 4 kèm câu hỏi vận dụng online tại đây: 

 

ÔN TẬP VỀ SỐ TỰ NHIÊN VÀ ĐẠI LƯỢNG KÈM BÀI TẬP VẬN DỤNG ONLINE - TOÁN LỚP 4

ÔN TẬP VỀ DẤU HIỆU CHIA HẾT VÀ BÀI TẬP VẬN DỤNG ONLINE - TOÁN LỚP 4

 

 

Các em xem livestream thầy Hiếu ôn tập các bài toán về phân số lớp 4 tại đây: