
Bài viết này thầy/cô mathx.vn sẽ tổng hợp gửi đến các em học sinh một số kiến thức cơ bản về các phép toán về phân số bao gồm: phép cộng; phép trừ; phép nhân; phép chia phân số và một số dạng toán cơ bản về phân số. Các em đọc kĩ lý thuyết và làm bài tập vận dụng online ở bên dưới. Chúc các em ôn tập tốt!
Quý phụ huynh và các em học sinh xem thêm một số bài viết về kiến thức lớp 4 tại đây:
TOÁN NÂNG CAO LỚP 4 - DẤU HIỆU CHIA HẾT CHO 2, 3, 5, 9
TOÁN NÂNG CAO LỚP 4 - MỘT SỐ BÀI TOÁN VỀ CHIA TỈ LỆ
Muốn cộng hai phân số có cùng mẫu số, ta cộng hai tử số với nhau và giữ nguyên mẫu số.
Ví dụ: \(\dfrac {3}{8} + \dfrac {2}{8} = \dfrac {3 + 2}{8} = \dfrac {5}{8}\)
Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.
Ví dụ: \(\dfrac {1}{2} + \dfrac {1}{3} = \dfrac {3}{6} + \dfrac {2}{6} = \dfrac {5}{6}\)
Chú ý: Khi thực hiện phép cộng hai phân số, nếu phân số thu được chưa tối giản thì ta rút gọn thành phân số tối giản.
+) Tính chất giao hoán: Khi đổi chỗ các phân số trong một tổng thì tổng không thay đổi.
a + b = b + a
+ Tính chất kết hợp: Khi cộng một tổng hai phân số với phân số thứ ba thì ta có thể cộng phân số thứ nhất với tổng của hai phân số còn lại.
(a + b) + c = a + (b + c)
+ Cộng với số 0: Phân số nào cộng với 00 cũng bằng chính phân số đó.
a + 0 = 0 + a = a
Dạng 1: Tính tổng của hai phân số
Phương pháp: Áp dụng quy tắc cộng hai phân số.
Dạng 2: Tính giá trị các biểu thức:
Áp dụng các quy tắc tính giá trị biểu thức như ưu tiên tính trong ngoặc trước, thực hiện phép tính nhân, chia trước, phép cộng trừ sau …
Dạng 3: So sánh
Phương pháp: Tính giá trị các biểu thức, sau đó áp dụng các quy tắc so sánh phân số.
Dạng 4: Tìm x
Phương pháp giải: Xác định xem x đóng vai trò nào, từ đó tìm được x theo các quy tắc đã học lớp lớp 3.
Dạng 5: Tính nhanh
Phương pháp giải: Áp dụng các tính chất của phép cộng phân số nhóm các phân số có thể tính toán dễ dàng.
Dạng 6: Toán có lời văn
Muốn trừ hai phân số có cùng mẫu số, ta trừ tử số của phân số thứ nhất cho tử số của phân số thứ hai và giữ nguyên mẫu số.
Ví dụ: \(\dfrac {5}{6} - \dfrac {3}{6} = \dfrac {5 - 3}{6} = \dfrac {2}{6} = \dfrac {1}{3}\)
Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi trừ hai phân số đó.
Ví dụ: \(\dfrac {4}{5} - \dfrac {2}{3} = \dfrac {12}{15} - \dfrac {10}{15} = \dfrac {2}{15}\)
Chú ý: Khi thực hiện phép trừ hai phân số, nếu phân số thu được chưa tối giản thì ta rút gọn thành phân số tối giản.
Dạng 1: Tính hiệu của hai phân số
Phương pháp: Áp dụng quy tắc trừ hai phân số.
Dạng 2: Tính giá trị các biểu thức:
Áp dụng các quy tắc tính giá trị biểu thức như ưu tiên tính trong ngoặc trước, thực hiện phép tính nhân, chia trước, phép cộng trừ sau …
Dạng 3: So sánh
Phương pháp: Tính giá trị các biểu thức, sau đó áp dụng các quy tắc so sánh phân số.
Dạng 4: Tìm x
Phương pháp giải: Xác định xem x đóng vai trò nào, từ đó tìm được x theo các quy tắc đã học lớp lớp 3.
Dạng 5: Toán có lời văn
Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
Ví dụ 1: \(\dfrac {4}{5} \times \dfrac {2}{3} = \dfrac {4 \times 2}{5 \times 3} = \dfrac {8}{15}\)
Ví dụ 2: \(\dfrac {9}{8} \times \dfrac {5}{18} = \dfrac {9 \times 5}{8 \times 18} = \dfrac {45}{144} = \dfrac {5}{16}\)
Lưu ý:
+) Sau khi làm phép nhân hai phân số, nếu thu được phân số chưa tối giản thì ta phải rút gọn thành phân số tối giản.
+) Khi nhân hai phân số, sau bước lấy tử số nhân tử số, mẫu số nhân mẫu số, nếu tử số và mẫu số cùng chia hết cho một số nào đó thì ta rút gọn luôn, không nên nhân lên sau đó lại rút gọn.
Ví dụ quay lại với ví dụ 2 ở bên trên, ta có thể làm như sau:
\(\dfrac {9}{8} \times \dfrac {5}{18} = \dfrac {9 \times 5}{8 \times 18} = \dfrac {9 \times 5}{8 \times 2 \times 9} = \dfrac {1 \times 5}{8 \times 2} = \dfrac {5}{16}\)
+) Tính chất giao hoán : Khi đổi chỗ các phân số trong một tích thì tích của chúng không thay đổi
a × b = b × a
+) Tính chất kết hợp: Khi nhân một tích hai phân số với phân số thứ ba, ta có thể nhân phân số thứ nhất với tích của hai phân số còn lại.
(a × b) × c = a × (b × c)
+ Tính chất phân phối: Khi nhân một tổng hai phân số với phân số thứ ba, ta có thể nhân lần lượt từng phân số của tổng với phân số thứ ba rồi cộng các kết quả đó lại với nhau.
(a + b) × c = a × c + b × c
+ Nhân với số 1: Phân số nào nhân với 11 cũng bằng chính phân số đó.
a × 1 = 1 × a = a
+ Nhân với số 0: Phân số nào nhân với 00 cũng bằng 00.
a × 0 = 0 × a = 0
Dạng 1: Tìm tích của hai phân số
Phương pháp: Áp dụng quy tắc nhân hai phân số.
Dạng 2: Tính giá trị các biểu thức:
Phương pháp giải: Áp dụng các quy tắc tính giá trị biểu thức như ưu tiên tính trong ngoặc trước, thực hiện phép tính nhân, chia trước, phép cộng trừ sau …
Dạng 3: So sánh
Phương pháp: Tính giá trị các biểu thức, sau đó áp dụng các quy tắc so sánh phân số.
Dạng 4: Tìm x
Phương pháp giải: Xác định xem x đóng vai trò nào, từ đó tìm được x theo các quy tắc đã học lớp lớp 3.
Dạng 5: Tính nhanh
Phương pháp giải: Áp dụng các tính chất của phép nhân phân số nhóm các phân số có thể tính toán dễ dàng.
Dạng 6: Toán có lời văn
Phân số đảo ngược của một phân số là phân số đảo ngược tử số thành mẫu số, mẫu số thành tử số.
Ví dụ: Phân số \(\dfrac {3}{2}\) gọi là phân số đảo ngược của phân số \(\dfrac {2}{3}\).
Muốn chia hai phân số, ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Ví dụ : \(\dfrac {7}{15} : \dfrac {2}{3} = \dfrac {7}{15} \times \dfrac {3}{2} = \dfrac {7 \times 3}{15 \times 2} = \dfrac {7 \times 1}{5 \times 2} = \dfrac {7}{10}\)
Dạng 1: Tìm thương của hai phân số
Phương pháp: Áp dụng quy tắc chia hai phân số.
Dạng 2: Tính giá trị các biểu thức:
Phương pháp giải: Áp dụng các quy tắc tính giá trị biểu thức như ưu tiên tính trong ngoặc trước, thực hiện phép tính nhân, chia trước, phép cộng trừ sau …
Dạng 3: So sánh
Phương pháp: Tính giá trị các biểu thức, sau đó áp dụng các quy tắc so sánh phân số.
Dạng 4: Tìm x
Phương pháp giải: Xác định xem x đóng vai trò nào, từ đó tìm được x theo các quy tắc đã học lớp lớp 3.
Dạng 5: Toán có lời văn
Bài toán: Một rổ cam có 12 quả. Hỏi \(\dfrac {2}{3}\) số cam trong rổ là bao nhiêu quả cam?
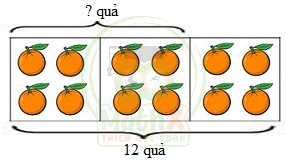
Nhận xét:
a) \(\dfrac {1}{3}\) số cam trong rổ là: 12 : 3 = 4 (quả)
\(\dfrac {2}{3}\) số cam trong rổ là: 4 × 2 = 8 (quả)
b) Ta có thể tìm \(\dfrac {2}{3}\) số cam trong rổ như sau:
12 × \(\dfrac {2}{3}\) =8 (quả )
Bài giải
\(\dfrac {2}{3}\) số cam trong rổ là:
12 x \(\dfrac {2}{3}\) = 8 (quả )
Đáp số: 8 quả cam.
Muốn tìm \(\dfrac {2}{3}\) của số 12 ta lấy số 12 nhân với \(\dfrac {2}{3}\).
Chú ý: Số cam được chia làm 3 phần và ta cần tìm 2 phần gồm bao nhiêu quả. Để tìm được 2 phần gồm bao nhiêu quả ta sẽ tìm 1 phần gồm bao nhiêu quả rồi nhân với 2. Do đó, để tìm \(\dfrac {2}{3}\) của 12 ta có thể lấy 12 chia cho 3 rồi nhân với 2.
Ta có lời giải như sau:
\(\dfrac {2}{3}\) số cam trong rổ là:
12 : 3 × 2 = 8 (quả )
Đáp số: 8 quả cam.
Bài toán: Biết \(\dfrac {2}{3}\) số cam trong rổ là 8 quả cam. Hỏi trong rổ có bao nhiêu quả cam?
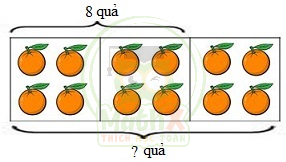
Nhận xét:
a) \(\dfrac {1}{3}\) số cam trong rổ là: 8 : 2 = 4 (quả)
Số cam trong rổ là: 4 × 3 = 12 (quả)
b) Ta có thể tìm số cam trong rổ như sau:
8 : 2 × 3 = 12 (quả )
Bài giải
Số cam trong rổ là:
8 : 2 × 3 = 12 (quả )
Đáp số: 12 quả cam.
Muốn tìm một số biết \(\dfrac {2}{3}\) của số đó là 8 ta lấy 8 chia cho 2 rồi nhân với 3.
Chú ý: Coi số cam trong rổ là 1 đơn vị. Theo đề bài ta có \(\dfrac {2}{3}\) số cam trong rổ là 8 quả cam. Do đó, để tìm số cam trong rổ ta có thể lấy 8 chia cho \(\dfrac {2}{3}\).
Ta có lời giải như sau:
Số cam trong rổ là:
8 : \(\dfrac {2}{3}\) = 8 x \(\dfrac {3}{2}\) = 12 (quả)
Đáp số: 12 quả cam.
Khi làm bài ta có thể làm một trong hai cách đã cho.
Trên đây thấy/cô MATHX vừa tổng hợp lại một số kiến thức của các phép tính về phân số kèm một số bài tập trắc nhiệm vận dụng. Các em học sinh hãy tiếp tục theo dõi Mathx để củng cố thêm vốn kiến thức toán học của bản thân nhé. Chúc các em học tốt!!
Tham khảo thêm nội dung kiến thức toán lớp 4 kèm câu hỏi vận dụng online tại đây:
CÁC KHÁI NIỆM CƠ BẢN VỀ PHẤN SỐ VÀ BÀI TẬP VẬN DỤNG ONLINE - TOÁN LỚP 4
TÍNH CHẤT GIAO HOÁN, TÍNH CHẤT KẾT HỢP, BIỂU THỨC CHỨA HAI, BA CHỮ - TOÁN LỚP 4