TÓAN NÂNG CAO LỚP 4 - MỘT SỐ BÀI TOÁN VỀ CHIA TỈ LỆ

Một số bài toán.

Bài 1. Đầu năm học nhà trường  mua cho khối 4 là 625 vở chia cho ba lớp. Biết 4A có 38 học sinh, lớp 4B có 42 học sinh, lớp 4C có 45 học sinh, mỗi em được mua số vở bằng nhau. Hỏi mỗi lớp mua bao nhiêu vở

Phân tích: Từ số học sinh 3 lớp ta tìm được tổng số học sinh khối 4. Vì mỗi học sinh được số vở bằng nhau nên ta tìm được số vở mỗi học sinh được mua, từ đó ta đi tính số vở mỗi lớp được mua.

Giải:

Số học sinh 3 lớp là: 38 + 42 + 45 = 125 (học sinh)

1 học sinh được mua số vở là: 625 : 125 = 5 (vở)

Lớp 4A được mua: 5 x 38 = 190 (vở)

Lớp 4B được mua: 5 x 42 = 210 (vở)

Lớp 4C được mua: 5 x 45 = 225 (vở)

Bài 2. Cô giáo chia 720 quyển vở cho 3 lớp. Biết 3 lần số vở của lớp 4A bằng hai lần số vở của lớp 4B, 5 lần số vở của lớp 4B bằng 3 lần số vở của lớp 4C. Tìm số vở của mỗi lớp.

Giải:

Theo đề bài ta có nếu biểu thị số vở 4B là 3 phần thì số vở của lớp 4A là 2 phần, số vở của lớp 4C là 5 phần. Ta có sơ đồ:

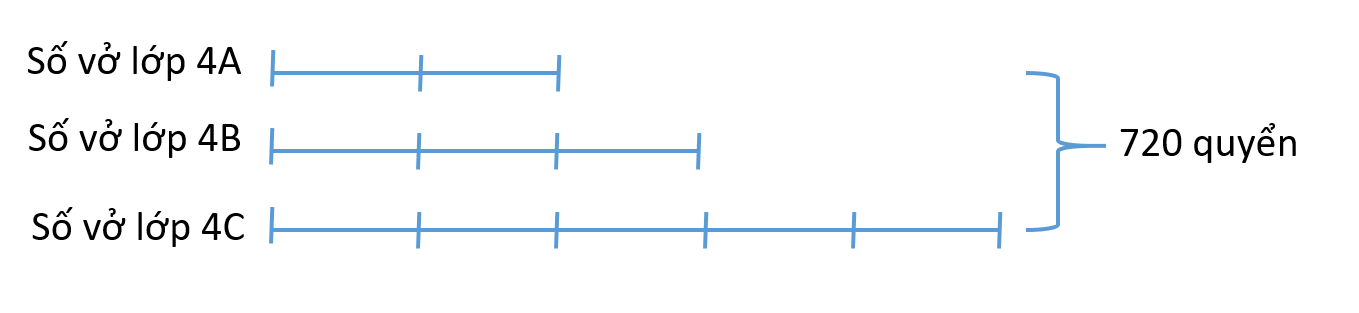
Tổng số phần bằng nhau là: 2 + 3 + 5 = 10 (phần)

Số vở 4A là: 720 : 10 x 2 = 144 (quyển)

Số vở 4B là: 144 : 2 x 3 = 216 (quyển)

Số vở 4C là: 216 : 3 x 5 = 360 (quyển)

 Bài 3. Hai đội thiếu niên tiền phong, đội 1 có 4 phân đội, đội 2 có 5 phân đội. Đội 1 kém đội 2 là 12 bạn. Biết số đội viên mỗi phân đội bằng nhau, tính xem cả hai đội có bao nhiêu đội viên?

Phân tích: Vì đội 2 nhiều hơn đội 1 là 1 phân đội, mà đội 2 nhiều hơn đội 1 là 12 bạn nên số bạn 1 phân đội là 12 bạn. Từ đó ta tính được số đội viên mỗi đội.

Giải:

Số phân đội của đội 2 hơn đội 1 là:

5 – 4 = 1 (phân đội)

Đội 1 kém đội 2 là 12 bạn, vậy 1 phân đội có 12 bạn.

Số đội viên đội 1 là: 12 x 4 = 48 (bạn)

Số đội viên đội 2 là: 12 x 5 = 60 (bạn)

Số đội viên của cả 2 đội là: 48 + 60 = 108 (bạn)

Bai 4. Một cửa hàng bán xà phòng, buổi sáng bán được 5 thùng, buổi chiều bán được 5 hộp. Biết buổi sáng bán nhiều hơn buổi chiều 100 gói và số gói ở mỗi thùng buổi sáng nhiều gấp đôi số gói ở mỗi hộp buổi chiều. Hỏi buổi sáng, buổi chiều bán được bao nhiêu gói xà phòng?

Giải:

Buổi sáng bán nhiều hơn buổi chiều: 5 x 2 – 5 = 5 (hộp buổi chiều)

1 hộp buổi chiều có số gói là: 100 : 5 = 20 (gói)

Số gói bán buổi sáng là: 20 x 5  x 2 = 200 (gói)

Số gói bán buổi chiều là: 20 x 5 = 100 (gói)

Bài 5. Có 4 đoàn xe, đoàn 1 gồm các xe, mỗi xe chở được 15 tạ, đoàn 2 gồm các xe, mỗi xe chở được 2 tấn, đoàn 3 gồm các xe, mỗi xe chở được 25 tạ và đoàn 4 gồm các xe, mỗi xe chở được 3 tấn. Cả bốn đoàn chở được 450 tạ gạo. Tính xem mỗi đoàn chở bao nhiêu tạ gạo, biết số xe của 4 đoàn bằng nhau.

Giải:

2 tấn = 20 tạ

3 tấn = 30 tạ.

Vì số xe của 4 đoàn bằng nhau nên ta giả sử mỗi đoàn đều có 1 xe thì số tạ gạo chở được là:

15 + 20 + 25 + 30 = 90 (tạ)

Số xe mỗi đoàn là: 450 : 90 = 5 (xe)

Đoàn 1 chở được: 15 x 5 = 75 (tạ)

Đoàn 2 chở được: 20 x 5 = 100 (tạ)

Đoàn 3 chở được: 25 x 5 = 125 (tạ)

Đoàn 4 chở được: 30 x 5 = 150 (tạ)

Bài 6. Trong một đợt kiểm tra, ba lớp 4A, 4B, 4C được tất cả 130 điểm 10. Biết số điểm 10 của lớp 4B gấp đôi số điểm 10 của lớp 4A và gấp rưỡi số điểm 10 của lớp 4C. Tính xem mỗi lớp có bao nhiêu điểm 10.

Giải:

Vì số điểm 10 của lớp 4B gấp đôi số điểm 10 của lớp 4A và gấp rưỡi số điểm 10 của lớp 4C và tổng số điểm 10 là 130 nên ta có sơ đồ : ( biểu thị số điểm 10 của lớp 4B là 6 phần bằng nhau), thì số điểm 10 của lớp 4A là 3 phần và số điểm 10 của lớp 4C là 4 phần như thế.

Số điểm 10 lớp 4A là:

130 : (6 + 4 + 3) x 3 = 30 (điểm)

Số điểm 10 lớp 4B là: 30 x 2 = 60 (điểm)

Số điểm 10 lớp 4C là: 130 – 60 – 30 = 40 (điểm)

Bài 7. Cô giáo mua vở cho học sinh 66 000 đồng, gồm ba loại 200 đồng, 400 đồng và 500 đồng một quyển. Số tiền mua vở mỗi loại đều bằng nhau. Hỏi mỗi loại có bao nhiêu quyển vở?

Giải:

Vì số tiền mua mỗi loại vở đều bằng nhau nên:

Số tiền mua mỗi loại vở là: 66 000 : 3 = 22 000 (đồng)

Số vở loại 200 đồng là: 22 000 : 200 = 110 (quyển)

Số vở loại 400 đồng là: 22 000 : 400 = 55 (quyển)

Số vở loại 500 đồng là: 22 000 : 500 = 44 (quyển)

Bài 8. Hai công nhân được thưởng 96 000 đồng. Biết 1/3 tiền thưởng của người thứ nhất bằng 1/5 tiền thưởng của người thứ hai. Hỏi mỗi người được thưởng bao nhiêu?

Giải:

Vì 1/3 số tiền thưởng của người thứ nhất bằng 1/5 số tiền thưởng của người thứ hai và tổng số tiền thưởng của 2 người là 96 000 đồng nên ta có sơ đồ:

Số tiền thưởng của người thứ nhất là: 96000 : (3 + 5 ) x 3 = 36 000 (đồng)

Số tiền thưởng của người thứ hai là: 96000 – 36000 = 60000 (đồng)

Bài 9. Cho 3 số có tổng bằng 550. Biết số thứ nhất bằng 1/2 số thứ ba, số thứ ba gấp 3 lần số thứ hai. Tìm ba số đó.

Giải:

Vì số thứ nhất bằng 1/2 số thứ 3, số thứ ba gấp 3 lần số thứ 2 nên biểu thị số thứ ba là 6 phần bằng nhau thì số thứ nhất sẽ là 3 phần như thế, số thứ hai sẽ là 2 phần như thế.

Tổng của chúng bằng 550 nên ta có sơ đồ:

Tổng số phần bằng nhau: 3 + 2 + 6 = 11 (phần)

Số thứ 1 là: 550 : 11 x 3 = 150

Số thứ 3 là: 150 x 2 = 300

Số thứ 2 là: 300 : 3 = 100

Bài 10. Hai nhà máy A và B có 2550 công nhân. Nếu thêm vào nhà máy B 200 người và giảm đi ở nhà máy A 200 người thì khi đó số công nhân ở nhà máy A sẽ bằng 1/2 số công nhân của nhà máy B. Tìm xem lúc đầu mỗi nhà máy có bao nhiêu công nhân.

Giải:

Thêm vào nhà máy B 200 người, giảm nhà máy A 200 người thì tổng số công nhân hai nhà máy vẫn là 2550 người. Số công nhân ở mỗi nhà máy sau khi đã thay đổi biểu thị theo sơ đồ sau:

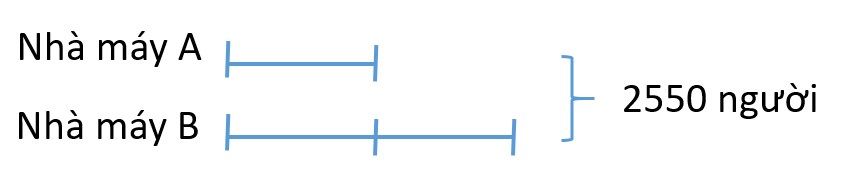
Số công nhân ở nhà máy A sau khi giảm 200 người là:

2550 : ( 1 + 2 ) = 850 (người)

Số công nhân lúc đầu ở nhà máy A là:

2550 – 1050 = 1500 (người)

Bài tập tự luyện.

Bài 1. An đi từ nhà tới trường mất 20 phút, từ trường đến câu lạc bộ thiếu niên mất 25 phút, quãng đường từ trường đến câu lạc bộ dài hơn quãng đường từ nhà đến trường là 325m. Hỏi từ nhà đến trường dài bao nhiêu mét? Từ trường đến câu lạc bộ dài bao nhiêu mét?

Bài 2. Tìm hai số có tổng là 1991 và thương của chúng là 1990.

Bài 3. Mẹ có 10 200 đồng gồm 3 loại tiền : loại 200 đồng, loại 500 đồng và 1000 đồng. Biết số tờ mỗi loại bằng nhau, tính xem mỗi loại có bao nhiêu đồng.

Bài 4. Một cửa hàng bán được 150 000 đồng tiền hàng, trong đó 1/3 tiền bán hàng may mặc bằng ½ tiền bán đồ nhôm và bằng 1/5 tiền bán đồ điện. Hỏi cửa hàng đó đã bán được bao nhiêu tiền hàng mỗi loại?

Bài 5. Có hai thùng kẹo. Nếu thêm 200 gói vào thùng thứ nhất thì số gói kẹo ở hai thùng bằng nhau, nếu thêm 300 gói vào thùng thứ hai thì số gói kẹo ở thùng thứ hai sẽ gấp đôi số kẹo ở thùng thứ nhất. Tìm số gói kẹo ở mỗi thùng.

Bài 6. Hai kho thóc, kho A có 3200 tấn, kho B có 5600 tấn. Nếu chuyển đi ở mỗi kho cùng một số thóc nào đó thì số thóc còn lại của kho B gấp đôi số thóc ở kho A. Tìm số thóc đã chuyển đi ở mỗi kho.

Bài 7. Lớp 4A và 4B chuẩn bị 96 000 đồng để mua phần thưởng cuối năm. Lớp 4A đã mua hết 10 000 đồng, lớp 4B mua hết 26 000 đồng khi đó số tiền còn lại của lớp 4A gấp đôi số tiền còn lại của lớp 4B. Hỏi lúc đầu mỗi lớp chuẩn bị bao nhiêu tiền mua phần thưởng?

Bài 8. Tổ An và Bình mua một số vở. Biết số vở của tổ An ít hơn số vở của tổ Bình là 30 quyển và 1/3 số vở tổ Bình bằng ½ số vở tổ An. Tìm số vở tổ An, tổ Bình đã mua.

Bài 9. An và Bình có một số tiền. Biết số tiền của Bình bằng ½ số tiền của An và Bình nếu thêm 200 đồng, An có thêm 1600 đồng thì lúc đó số tiền của An sẽ gấp 3 lần số tiền của Bình. Tìm số tiền lúc đầu của mỗi người.

Bài 10. Trong một trường ngoại ngữ học buổi tối số người học tiếng Đức bằng ½ số người học tiếng Pháp, số người học tiếng Pháp bằng 1/3 số người học tiếng Anh. Hỏi mỗi ngoại ngữ có bao nhiêu người học, biết số người học tiếng Anh nhiều hơn số người học tiếng Đức là 100 người?

Bài 11. Ba người đi bằng ba loại xe khác nhau từ A đến B. Thời gian người thứ nhất đi bằng 1/3 thời gian người thứ ba đi và bằng 1/2 thời gian người thứ hai đi. Biết 1 giờ người thứ hai đi được 24km và thời gian người thứ ba đi là 135 phút, tính quãng đường AB.