Trường Toán Online MATHX
MATHX.VN biên soạn bộ đề kiểm tra giữa kì 2 Toán 7 năm 2023 kèm lời giải chi tiết giúp các em học sinh nhanh chóng làm quen với cấu trúc đề thi, ôn tập để đạt được kết quả cao trong kì thi giữa học kì sắp tới. Mời các em cùng tham khảo dưới đây!
Phụ huynh và các em học sinh xem thêm đề thi giữa kì 2 môn toán lớp 7 năm học 2023 - 2024 tại đây:
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 1
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 2
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 3
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 4
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 5
Câu 6: Cho ABCD là hình chữ nhật như hình vẽ, điểm E nằm trên cạnh CD. Khẳng định nào sau đây là sai?
Bài 1: Tìm số hữu tỉ x trong các tỉ lệ thức sau:
a) \({\dfrac{-6}{x}}={\dfrac{9}{-15}}\)
b) \({\dfrac{-4}{x}}={\dfrac{x}{-49}}\)
Lời giải:
a) Ta có: \({\dfrac{-6}{x}}={\dfrac{9}{-15}}\)
Suy ra \((-6)\cdot(-15)=9.x\)
\(x={\dfrac{\left(-6\right)\cdot\left(-15\right)}{9}}=10\)
Vậy x = 10.
b) Ta có: \({\dfrac{-4}{x}}={\dfrac{x}{-49}}\)
Suy ra \(\left(-4\right)\left(-49\right)=x.x\)
\(x^2 = 196\)
x = ± 14
Vậy x = ± 14.
Bài 2:
a) Cho \({\dfrac{a}{b}}={\dfrac{6}{5}}\). Tìm a, b biết: a – b = 3
b) Cho \({\dfrac{x}{2}}={\dfrac{y}{3}}=\dfrac{z}{5}\). Tìm x, y, z biết x - y + z = 32
Lời giải:
a) Ta có: \({\dfrac{a}{b}}={\dfrac{6}{5}}\) suy ra \({\dfrac{a}{6}}={\dfrac{b}{5}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\({\dfrac{a}{6}}\,=\,{\dfrac{b}{5}}\,=\,{\dfrac{a-b}{6-5}}\,=\,{\dfrac{3}{1}}\,=\,3.\)
Suy ra \(a=3.6=18;b=3.5=15.\)
Vậy a = 16; b = 15.
b) Ta có: \({\dfrac{x}{2}}={\dfrac{y}{3}}=\dfrac{z}{5}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\({\dfrac{x}{2}}\,\equiv\,{\dfrac{y}{3}}\,=\,{\dfrac{z}{5}}\,=\,{\dfrac{x-y+z}{2-3+5}}\,=\,{\dfrac{32}{4}}\,=\,8.\)
Suy ra \(x=8.2=16\)
\(y = 8.3 = 24\)
\(z = 8.5 = 40\)
Vậy x = 16; y = 24; z = 40.
Bài 3: Ba đơn vị cùng vận chuyển 700 tấn hàng. Đơn vị A có 10 xe trọng tải mỗi xe là 5 tấn; đơn vị B có 20 xe trọng tải mỗi xe là 4 tấn; đơn vị C có 14 xe trọng tải mỗi xe là 5 tấn. Hỏi mỗi đơn vị vận chuyển được bao nhiêu tấn hàng, biết mỗi xe đều chở một số chuyến như nhau?
Lời giải:
Gọi x, y, z (tấn) lần lượt là khối lượng hàng các đơn vị A, B, C vận chuyển (x, y, z > 0).
Theo đề bài ta suy ra: \(\dfrac{x}{50}\;\equiv\;\dfrac{y}{80}\;=\dfrac{z}{70}\) và x + y + z = 700.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{50}\;\equiv\;\dfrac{y}{80}\;=\dfrac{z}{70}\) = \(\dfrac{x+y+z}{50+80+70} = \dfrac{700}{200} = 3,5\)
x = 175; y = 280; z = 245
Vậy khối lượng hàng các đơn vị A, B, C vận chuyển lần lượt là 175; 280; 245 tấn.
Bài 4: Cho góc xOy khác góc bẹt có Ot là tia phân giác. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot và cắt Ox và Oy theo thứ tự A và B.
a) Chứng minh OA = OB.
b) Lấy điểm C nằm giữa O và H. Chứng minh \(\widehat{A C H}=\widehat{H C B}\)
c) AC cắt Oy ở D. Trên tia Ox lấy điểm E sao cho OE = OD. Chứng minh ba điểm B, C, E thẳng hàng.
Lời giải:
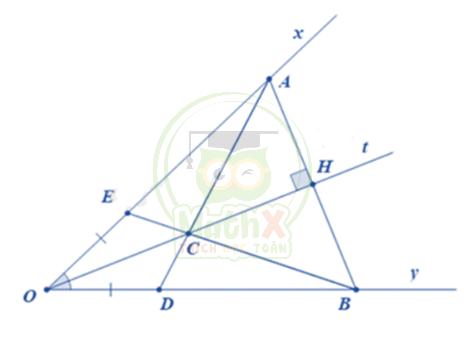
a) Xét tam giác AHO và tam giác BHO có:
\({\widehat{A O H}}={\widehat{B O H}}\) (Ot là tia phân giác của \(\widehat{A O H})\)
OH chung
\({\widehat{AHO}}={\widehat{B HO}}\) \((=90^{0})\)
=> ΔAHO = ΔBHO (g.c.g)
=> OA = OB (hai cạnh tương ứng) (đpcm)
b) ΔAHO = ΔBHO => AH = HB (hai cạnh tương ứng)
Xét tam giác AHC và tam giác BHC có:
HC chung
\({\widehat{AHC}}={\widehat{B HC}}\) \((=90^{0})\)
AH = HB
=> ΔAHC = ΔBHC (hai cạnh góc vuông)
=> \({\widehat{ACH}}={\widehat{HCB}}\) (hai góc tương ứng)
c) Xét tam giác OCE và OCD có:
OE = OD
\({\widehat{EOC}}={\widehat{DOC}}\)
OC chung
Suy ra ∆OEC = ∆ODC (c.g.c)
Suy ra EC = DC (hai cạnh tương ứng)
Ta có OA = OB và OE = OD nên AE = BD.
Xét ∆ECA = ∆DCB có:
EC = ED (cmt)
EA = DB (cmt)
CA = CB (∆AHC = ∆BHC)
=> ∆ECA = ∆DCB (c.c.c)
=> \({\widehat{ECA}}={\widehat{DCB}}\) (hai góc tương ứng)
Mặt khác \({\widehat{ECA}}={\widehat{ECD}}\) = \(180^o\) (vì AC cắt Oy tại D)
=> \({\widehat{DCB}}={\widehat{ECD}}=180^o\) hay B, C, E thẳng hàng (đpcm).
Bài 5: Cho tỉ lệ thức \({\dfrac{a}{b}}={\dfrac{c}{d}}\). Chứng minh \(\dfrac{a b}{c d}\,=\,\dfrac{a^{2}-b^{2}}{c^{2}-d^{2}}.\)
Lời giải:
Đặt \({\dfrac{a}{b}}={\dfrac{c}{d}}\) = \(k\Rightarrow\left\{\begin{array}{l}{{a=b k}}\\ {{c=d k}}\end{array}\right.\)
Do đó ta có:
\({\dfrac{ac}{bd}}={\dfrac{bkdk}{bd}} = k^2 (1)\)
Ta cũng có:
\(\dfrac{a^{2}+c^{2}}{b^{2}+d^{2}}\,=\,\dfrac{(b k)^{2}+(d k)^{2}}{b^{2}+d^{2}}\,=\,\dfrac{b^{2}k^{2}+d^{2}k^{2}}{b^{2}+d^{2}}\,\) = \(\dfrac{k^{2}(b^{2}+d^{2})}{b^{2}+d^{2}}\ =k^{2}(2)\)
Từ (1) và (2) suy ra:
\(\dfrac{ac}{bd}=\dfrac{a^{2}+c^{2}}{b^{2}+d^{2}}\,\) = \((k^2)\) (đpcm)
Trên đây MATHX đã hướng dẫn các em giải đề thi giữa kì 2 môn toán lớp 7 năm học 2023 - 2024 - đề 5. Ngoài ra các bậc phụ huynh cần cho con em mình học đúng phương pháp và tham khảo các khóa học online tại MATHX.VN để giúp con tự tin chinh phục môn toán nhé.