
MATHX.VN biên soạn bộ đề kiểm tra giữa kì 2 Toán 7 năm 2023 kèm lời giải chi tiết giúp các em học sinh nhanh chóng làm quen với cấu trúc đề thi, ôn tập để đạt được kết quả cao trong kì thi giữa học kì sắp tới. Mời các em cùng tham khảo dưới đây!
Phụ huynh và các em học sinh xem thêm đề thi giữa kì 2 môn toán lớp 7 năm học 2023 - 2024 tại đây:
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 1
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 2
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 3
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 4
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 5
Bài 1. Tìm x biết:
a) \(x-{\dfrac{2}{5}}={\dfrac{-9}{10}}\)
b) \({\dfrac{3}{4}}+{\dfrac{1}{4}}x={\dfrac{-5}{6}}\)
c) \({\dfrac{x-1}{3}}={\dfrac{2-x}{-2}}\)
Lời giải:
a) \(x-{\dfrac{2}{5}}={\dfrac{-9}{10}}\)
\(x={\dfrac{-9}{10}}+{\dfrac{2}{5}}\)
\(x={\dfrac{-9+2.2}{10}}\)
\(x={\dfrac{-5}{10}}={\dfrac{-1}{2}}\)
Vậy x = \(\dfrac{-1}{2}\)
b) \({\dfrac{3}{4}}+{\dfrac{1}{4}}x={\dfrac{-5}{6}}\)
\({\dfrac{1}{4}}x={\dfrac{-5}{6}}-{\dfrac{3}{4}}\)
\({\dfrac{1}{4}}x={\dfrac{-5.2-3.3}{12}}\)
\({\dfrac{1}{4}}x={\dfrac{-19}{12}}\)
\(x={\dfrac{-19}{12}}:{\dfrac{1}{4}}\)
\(x={\dfrac{-19}{3}}\)
Vậy \(x={\dfrac{-19}{3}}\)
c) \({\dfrac{x-1}{3}}={\dfrac{2-x}{-2}}\)
\(-2\ (x-1)=3\left(2-x\right)\)
\(-2x+2=6-3x\)
\(-2x+3x=6-2\)
\(x = 4\)
Vậy \(x = 4\)
Bài 2. Tính chu vi của hình chữ nhật biết rằng chiều dài và chiều rộng của hình chữ nhật đó lần lượt tỉ lệ với 5 ; 3 và hai lần chiều dài hơn ba lần chiều rộng là 8 cm.
Lời giải:
Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là x,y (cm) (điều kiện: x,y > 0.
Theo đề bài: chiều dài và chiều rộng của hình chữ nhật đó lần lượt tỉ lệ với 5;3 nên ta có: \({\dfrac{x}{5}}={\dfrac{y}{3}}\)
Hai lần chiều dài hơn ba lần chiều rộng là 8 cm nên 2x − 3y = 8
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\({\dfrac{x}{5}}={\dfrac{y}{3}}={\dfrac{2x}{10}}={\dfrac{3y}{9}}={\dfrac{2x-3y}{10-9}}={\dfrac{8}{1}}=8\)
Khi đó, \({\dfrac{x}{5}}\,=\,8\,\Rightarrow\,x\,=40\) (tmđk)
\({\dfrac{y}{3}}\,=\,8\,\Rightarrow\,y\,=24\) (tmđk)
Chu vi của hình chữ nhật là: \(2\left(x+y\right)=2\left(40+24\right)=128\left(\mathrm{cm}\right)\)
Bài 3. Cho hai đa thức: \(P\left(x\right)=x^{3}\ -2x^{2}+x-2;\) \(Q\left(x\right)=2x^{3}\ -4x^{2}+3x-6\)
a) Tính P(x) - Q(x)
b) Chứng tỏ rằng x = 2 là nghiệm của cả hai đa thức P(x) và Q(x).
Lời giải:
a) Ta có P(x) – Q(x) = (\(x^3\) – 2\(x^2\) + x – 2) – (2\(x^3\) – 4\(x^2\) + 3x – 6)
= \(x^3\) – 2\(x^2\) + x – 2 – 2\(x^3\) + 4\(x^2\) – 3x + 6
= (\(x^3\) – 2\(x^3\)) + (4\(x^2\) – 2\(x^2\)) + (x – 3x) + (6 – 2)
= – \(x^3\)– 2\(x^2\) – 2x + 4.
Vậy P(x) – Q(x) = – \(x^3\)– 2\(x^2\) – 2x + 4.
b) Thay x = 2 vào đa thức P(x), ta có:
P(2) = \(2^3\) – 2 . \(2^2\) + 2 – 2 = 8 – 2 . 4 + 0 = 8 – 8 = 0;
Thay x = 2 vào đa thức Q(x), ta có:
Q(2) = 2 . \(2^3\) – 4 . \(2^2\) + 3 . 2 – 6 = 2 . 8 – 4 . 4 + 6 – 6
= 16 – 16 + 0 = 0.
Vậy x = 2 là nghiệm của cả hai đa thức P(x) và Q(x).
Bài 4. Cho ΔABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho DM = MA
a) Chứng minh ΔAMB = ΔDMC
b) Trên tia đối của tia CD, lấy điểm I sao cho CI = CA, qua điểm I vẽ đường thẳng song song với AC cắt A tại E. Chứng minh ΔACE = ΔICE từ đó suy ra ΔACE là tam giác vuông cân.
Lời giải:
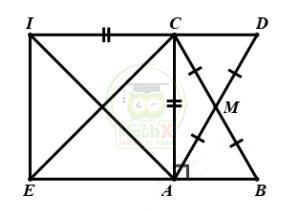
a) ΔABC vuông tại A,AM là đường trung tuyến ⇒ CM = BM
Ta có: ∠CMD = ∠AMB (hai góc đối đỉnh)
Xét ΔAMB và ΔDMC có:
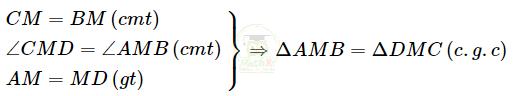
b) Ta có: ΔAMB = ΔDMC (cmt) ⇒ ∠ABM = ∠DCM (hai góc tương ứng)
Mà hai góc ∠ABM; ∠DCM ở vị trí so le trong
=> AB // CD
Mà AB ⊥ AC (ΔABC vuông tại A)
⇒ CD ⊥ AC tại C ⇒ EI ⊥ CD tại I (vì EI // AC) hay ∠EIC = 90°
Xét ΔACE và ΔICE có:
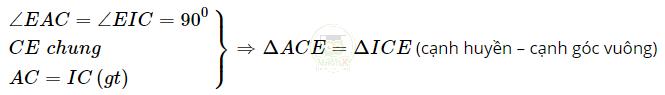
⇒ ∠ACE = ∠ICE (hai góc tương ứng)
Mà ∠ICE = ∠AEC (vì AB // CD)
⇒ ∠ACE = ∠AEC
⇒ ΔACE vuông cân tại A (∠EAC = 90°)
Bài 5. Cho đa thức \(f(x)\) thỏa mãn \(f\left(x\right)+x. f\left(-x\right)=x+1\) với mọi giá trị của x tính \(f(1)\)
Lời giải:
Với x = -1, ta có: \(f\left(-1\right)+\left(-1\right)\cdot f\left(1\right)=-1+1\)
=> \(f\left(-1\right)-f\left(1\right)=0\)
=> \(f\left(-1\right)=f\left(1\right)\)
Với x = -1, ta có: \(f\left(-1\right)+\left(-1\right)\cdot f\left(1\right)=1+1\)
\(\Rightarrow f\left(1\right)+f\left(-1\right)=2\)
Suy ra, \(f\left(1\right)+f\left(1\right)=2\)
\(=> 2f (1) = 2\)
=> \(f (1) = 1\)
Vậy \(f (1) = 1\)
Trên đây MATHX đã hướng dẫn các em giải đề thi giữa kì 2 môn toán lớp 7 năm học 2023 - 2024 - đề 2. Ngoài ra các bậc phụ huynh cần cho con em mình học đúng phương pháp và tham khảo các khóa học online tại MATHX.VN để giúp con tự tin chinh phục môn toán nhé.