
Toán học luôn là bộ môn mang tính chất phát triển não bộ về khả năng tư duy, sáng tạo. Chính vì vậy mà các bậc phụ huynh cũng như thầy cô giáo luôn hướng tới rèn luyện học sinh các bài tập phát triển tư duy. Nhằm giúp các em tiếp cận gần hơn với Toán tư duy, đội ngũ MATHX biên soạn các bài toán tư duy về chủ đề SỐ THẬP PHÂN - Toán tư duy lớp 5 kèm bài tập vận dụng online có đáp án. Mời ba mẹ và các con cùng tham khảo!
Phụ huynh và các con tham khảo thêm một số nội dung toán tư duy lớp 5 kèm bài tập tại MATHX dưới đây nhé:
100 BÀI TRẮC NGHIỆM TOÁN TƯ DUY LỚP 5
Phân số
- Rút gọn phân số
Bước 1: Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
Bước 2: Chia tử số và mẫu số cho số đó.
Bước 3: Cứ làm như thế cho đến khi nhận được phân số tối giản
\(\dfrac{{15}}{{20}} = \dfrac{{15:5}}{{20:5}} = \dfrac{3}{4}\)
Lưu ý: Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn 1, hay phân số tối giản là phân số không thể rút gọn được nữa
Ví dụ: \(\dfrac{{64}}{{72}} = \dfrac{{64:8}}{{72:8}} = \dfrac{8}{9}\)
- Quy đồng mẫu số
+ Các phân số có mẫu số không chia hết cho nhau
Cho 2 phân số: \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\)
Quy đồng mẫu số
\(\dfrac{a}{b}\) = \(\dfrac{a\times d}{b\times d}\)
\(\dfrac{c}{d}\) = \(\dfrac{c\times b}{d\times b}\)
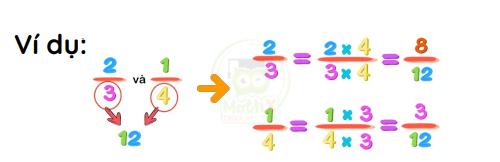
- Các phân số có mẫu số chia hết cho nhau
Bước 1: Lấy b : d = m
Bước 2: Nhân cả tử và mẫu của phân số \(\dfrac{c}{d}\) với m ta được:
\(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) = \(\dfrac{c\times m}{d\times m}\)

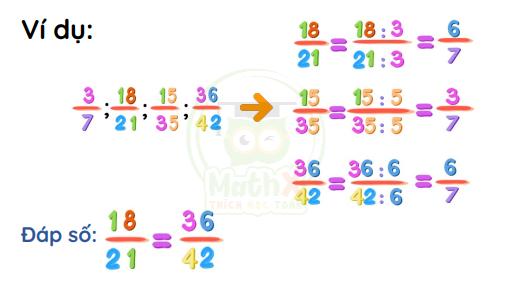
- Tìm các phân số bằng nhau
Cách 1: Nhân cả tử số và mẫu số với 1 số khác 0.
Cách 2: Chia cả tử số và mẫu số với 1 số khác 0.
- Phân số thập phân
Các phân số có mẫu số là 10; 100; 1000; ... gọi là các phân số thập phân
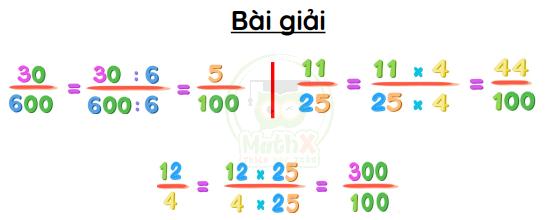
Ví dụ: Viết các phân số thành phân số thập phân
\(\dfrac{30}{600}\) ; \(\dfrac{11}{25}\) ; \(\dfrac{12}{4}\)
- So sánh phân số
+ Trong hai phân số cùng mẫu số:
Phân số nào có tử số bé hơn thì bé hơn.
Phân số nào có tử số lớn hơn thì lớn hơn. Nếu tử số bằng nhau thì hai phân số đó bằng nhau.
Ví dụ: \(\dfrac{2}{10}\) < \(\dfrac{3}{10}\)
+ Trong hai phân số khác mẫu số
Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó rồi so sánh các tử số của chúng.
Ví dụ:

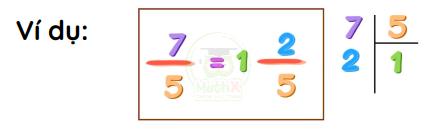
- Chuyển phân số thành hỗn số
Thực hiện phép chia tử số cho mẫu số
Giữ nguyên mẫu số của phần phân số
Tử số = số dư của phép chia tử số cho mẫu số
Phần nguyên = thương của phép chia tử số cho mẫu số
- So sánh hỗn số
Cách 1: Chuyển hỗn số về phân số
Muốn so sánh hai hỗn số, ta chuyển hai hỗn số về dạng phân số rồi so sánh hai phân số vừa chuyển đổi.
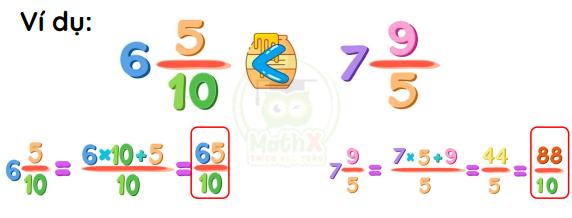
Cách 2: So sánh phần nguyên trước, rồi so sánh phần phân số
- Hỗn số nào có phần nguyên lớn hơn thì lớn hơn
- Hỗn số nào có phần nguyên nhỏ hơn thì nhỏ hơn
- Nếu hai phần nguyên bằng nhau thì ta so sánh phần phân số, hỗn số nào có phần phân số lớn hơn thì lớn hơn và ngược lại hỗn số nào có phần phân số nhỏ hơn thì nhỏ hơn.
Đọc – Viết số thập phân

Đọc là: ba trăm bảy mươi lăm phẩy bốn trăm linh sáu
Chuyển các phân số thành số thập phân
Nếu phân số đã cho chưa là số thập phân thì ta chuyển các phân số thành phân số thập phân rồi chuyển thành số thập phân.
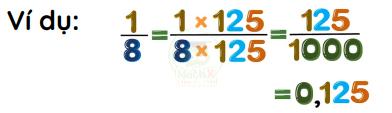
Viết hỗn số thành số thập phân
Đổi hỗn số về dạng phân số thập phân, sau đó chuyển thành số thập phân.
Ví dụ: \(9\dfrac{4}{100}=9,04\)
Số thập phân bằng nhau
0,9 = 0,90
0,40 = 0,4
Nếu viết thêm chữ số 0 vào bên phải phần thập phân của một số thập phân thì được một số thập phân bằng nó.
Nếu một số thập phân có chữ số 0 ở tận cùng bên phải phần thập phân thì bỏ chữ số 0 đó đi, ta được một số thập phân bằng nó.
So sánh số thập phân
35,7 > 35,698
(phần nguyên bằng nhau, hàng phần mười có 7 > 6)
|
- So sánh phần nguyên của hai số - So sánh phần phập phân, lần lượt từ: hàng phần mười => hàng phần trăm => hàng phần nghìn,… - Hai số có phần nguyên và phần thập phân bằng nhau thì hai số đó bằng nhau. |
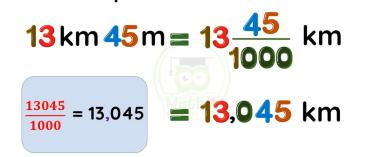
Viết các số đo độ dài, khối lượng… dưới dạng số thập phân
– Tìm mối liên hệ giữa hai đơn vị đo đã cho.
– Chuyển số đo độ dài đã cho thành phân số thập phân có đơn vị đo lớn hơn.
– Chuyển từ số đo độ dài dưới dạng phân số thập phân thành số đo độ dài tương ứng dưới dạng số thập phân có đơn vị lớn hơn.
\(\dfrac{\begin{array}{l} 1,84\\ + \\ 2,45 \end{array}}{{4,29}} \)
Một cộng hai số thập phân ta làm như sau:
- Viết số hạng này dưới số hạng kia sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.
- Cộng như cộng các số tự nhiên.
- Viết dấu phẩy ở tổng thẳng cột với các dấu phẩy của các số hạng.
\(\dfrac{\begin{array}{l} 4,29\\ - \\ 2,45 \end{array}}{{1,84}} \)
Muốn trừ một số thập phân cho một số thập phân ta làm như sau:
- Viết số trừ dưới số bị trừ sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.
- Trừ như trừ các số tự nhiên.
- Viết dấu phẩy ở hiệu thẳng cột với các dấu phẩy của số bị trừ và số trừ.
- Nhân một số thập phân với một số tự nhiên
\(\dfrac{\begin{array}{l} 1,2\\ \times \\ 3 \end{array}}{{3,6}} \)
Muốn nhân một số thập phân với một số tự nhiên ta làm như sau:
- Nhân như nhân các số tự nhiên
- Đếm xem trong phần thập phân của số thập phân có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.
- Nhân một số thập phân với 10, 100, 1000,...
\(\dfrac{\begin{array}{l} 27,867\\ \times \\ 10 \end{array}}{{278,670}} \)
Muốn nhân một số thập phân với 10, 100, 1000,.. ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên phải một, hai, ba, … chữ số.
- Nhân một số thập phân với một số thập phân
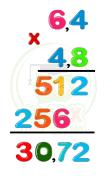
Muốn nhân một số thập phân với một số thập phân ta làm như sau:
- Nhân như nhân các số tự nhiên
- Đếm xem trong phần thập phân của cả hai thừa số có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiều chữ số kể từ phải sang trái.
- Nhân một số thập phân với 0,1; 0,01; 0,001; …
\(\dfrac{\begin{array}{l} 142,57\\ \times \\ 0,1 \end{array}}{{14,257}} \)
Muốn nhân một số thập phân với 0,1; 0,01; 0,001;...ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba,... chữ số.
+ Chia một số thập phân cho một số tự nhiên

Muốn chia một số thập phân cho một số tự nhiên ta làm như sau:
- Chia phần nguyên cúa số bị chia cho số chia.
- Viết dau phẩy vào bên phải thương đã tìm được trước khi lấy chữ số đầu tiên ở phần thập phân của số bị chia để tiếp tục thực hiện phép chia.
- Tiếp tục chia với từng chữ số ở phần thập phân của số bị chia.
+ Chia một số thập phân cho 10, 100, 1000,...
Muốn chia một số thập phân cho 10, 100, 1000, … ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.
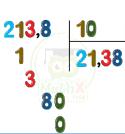
+ Chia một số thập phân cho một số thập phân
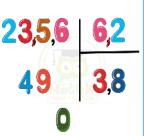
Muốn chia một số thập phân cho một số thập phân ta làm như sau:
- Đếm xem có bao nhiêu chữ số ở phần thập phân của số chia thì chuyển dấu phẩy ở số bị chia sang bên phải bấy nhiêu chữ số.
- Bỏ dấu phẩy ở số chia rồi thực hiện phép chia như chia cho số tự nhiên.
+ Chia một số tự nhiên cho một số tự nhiên mà thương tìm được là một số thập phân.
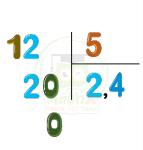
Khi chia một số tự nhiên cho một số tự nhiên mà còn dư, ta tiếp tục chia như sau:
- Viết dấu phẩy vào bên phải số thương.
- Viết thêm vào bên phải số dư một chữ số 0 rồi chia tiếp.
- Nếu còn dư nữa, ta lại viết thêm vào bên phải số dư mới một chữ số 0 rồi tiếp tục chia, và có thể cứ làm như thế mãi.
+ Chia một số tự nhiên cho một số thập phân

Muốn chia một số tự nhiên cho một số thập phân ta làm như sau: -Đếm xem có bao nhiêu chữ số ở phần thập phân của số chia thì viết thêm vào bên phải số bị chia bấy nhiêu chứ số 0. -Bỏ dấu phẩy ở số chia rồi thực hiện phép chia như chia các số tự nhiên.
Đối với dạng toán này các em đã được học cách tìm tỉ số phần trăm của hai số và làm một số bài toán mẫu ở sách giáo khoa. Dựa trên bài toán mẫu giáo viên hướng dẫn giải các bài tập nâng cao.
Ví dụ:

Trên đây là những nội dung lý thuyết và bài tập vận dụng về PHÂN SỐ THẬP PHÂN - Toán tư duy lớp 5. Hi vọng những chia sẻ vừa rồi của MATHX sẽ giúp các em có thêm hành trang vững bước trong quá trình học tập của bản thân. Chúc các em học tập hiệu quả!!
Ngoài ra các em có thể tham khảo thêm các khóa học Toán Lớp 4 gồm các khóa học ôn tập hè, luyện toán tiếng anh, toán tư duy, toán nâng cao, luyện đề học sinh giỏi… trong link sau: Các khóa học toán lớp 5 tại MATHX
Lưu ý: Các em cần Tạo Tài Khoản và Đăng Nhập để có thể xem được những nội dung này