GIẢI CHI TIẾT ĐỀ THI HỌC KÌ 1 MÔN TOÁN LỚP 9 THCS MARIE CURIE NĂM HỌC 2023 2024 - MATHX

 

MATHX biên soạn gửi tới các em hướng dẫn giải chi tiết đề thi học kì 1 môn toán lớp 9 trường THCS marie curie năm học 2023 2024. Các em học sinh tải để về làm trước sau đó so sánh kết quả và cách giải chi tiết trong bài viết này. Chúc các em học tập tốt!

 

 

 

ĐỀ KIỂM TRA HỌC KÌ 1 THCS MARIE CURIE

(ĐÁP ÁN + LỜI GIẢI CHI TIẾT)

Môn thi: Toán lớp 9

Năm học: 2023 - 2024

Thời gian làm bài: 90 phút

 

HƯỚNG DẪN GIẢI CHI TIẾT

 

 

Câu I: Thực hiện phép tính:

a) \(3{\sqrt{\dfrac{1}{3}}}+4{\sqrt{12}}-5{\sqrt{27}}\)

b) \({\dfrac{3+2\sqrt{3}}{\sqrt{3}}}-{\dfrac{2}{\sqrt{3}-1}}\)

a)

Hướng dẫn:

\(\begin{array}{c}{{3\sqrt{\dfrac13}+4\sqrt{12}-5\sqrt{27}=3\sqrt{\dfrac3{{3^2}} }+4\sqrt{43}-5\sqrt{93}}}\\ {{=\sqrt{3}+8\sqrt{3}-15\sqrt{3}}}\end{array}\)

\(=-6{\sqrt{3}}\)

 

b)

Hướng dẫn:

\({\dfrac{3+2\sqrt{3}}{\sqrt{3}}}-{\dfrac{2}{\sqrt{3}-1}}={\dfrac{\sqrt{3}\left(\sqrt{3}+2\right)}{\sqrt{3}}}-{\dfrac{2\left(\sqrt{3}+1\right)}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}}=\sqrt{3}+2-{\dfrac{2\left(\sqrt{3}+1\right)}{2}}\)

\(={\bigg(}{\sqrt{3}}+2{\bigg)}-{\bigg(}{\sqrt{3}}+1{\bigg)}={\sqrt{3}}+2-{\sqrt{3}}-1=1\)

 

2. Giải phương trình \({\sqrt{x-1}}+{\sqrt{9_{X}-9}}-{\sqrt{4x-4}}=4\).

Hướng dẫn:

 \({\sqrt{x-1}}+{\sqrt{9_{X}-9}}-{\sqrt{4x-4}}=4\) (x ≥ 1)

\(\Leftrightarrow \ \)\({\sqrt{\mathbf{x}-1}}+{\sqrt{9\left(\mathbf{x}-1\right)}}-{\sqrt{4\left(\mathbf{x}-1\right)}}=4\)

\(\Leftrightarrow \ \)\({\sqrt{\mathbf{x}}}-1+3{\sqrt{\mathbf{x}-1}}-2{\sqrt{\mathbf{x}-1}}=4\) 

\(\Leftrightarrow \ \)\(2{\sqrt{\mathbf{x}-1}}=4\)

\(\Leftrightarrow \ \)\({\sqrt{\mathbf{x}-1}}=2\)

\(\Leftrightarrow \ \)x - 1 = 4 

\(\Leftrightarrow \ \)x = 5 (TMĐK)

 

 

 

Câu II.  Cho hai biểu thức A = \(\mathrm{A={\dfrac{\mathrm{x}+3}{\sqrt{\mathrm{x}+1}}}}\) và \(\mathbf{B}={\dfrac{1}{\sqrt{\mathbf{x}-1}}}+{\dfrac{\sqrt{\mathbf{x}}}{\sqrt{\mathbf{x}+1}}}+{\dfrac{2{\sqrt{\mathbf{x}}}}{1-\mathbf{x}}}\ \left(\mathbf{x}\geq0,\mathbf{x}\neq1\right)\)

1. Rút gọn B.

Hướng dẫn:

\(\mathbf{B}={\dfrac{1}{\sqrt{\mathbf{x}-1}}}+{\dfrac{\sqrt{\mathbf{x}}}{\sqrt{\mathbf{x}+1}}}+{\dfrac{2{\sqrt{\mathbf{x}}}}{1-\mathbf{x}}}\ \left(\mathbf{x}\geq0,\mathbf{x}\neq1\right)\)

\(={\dfrac{1}{\sqrt{\mathbf{x}-1}}}+{\dfrac{\sqrt{\mathbf{x}}}{\sqrt{\mathbf{x}+1}}}-{\dfrac{2{\sqrt{\mathbf{x}}}}{\left({\sqrt{\mathbf{x}}}-1\right)\left({\sqrt{\mathbf{x}}}+1\right)}}\)

\(={\dfrac{\left({\sqrt{x}}+1\right)+{\sqrt{x}}\left({\sqrt{x}}-1\right)-2{\sqrt{x}}}{\left({\sqrt{x}}-1\right)\left({\sqrt{x}}+1\right)}}\)

\(={\dfrac{\sqrt{\mathbf{x}}-1+\mathbf{x}-{\sqrt{\mathbf{x}}}-2{\sqrt{\mathbf{x}}}}{\left({\sqrt{\mathbf{x}}}-1\right)\left({\sqrt{\mathbf{x}}}+1\right)}}\)

=\(\textstyle{\dfrac{x-2{\sqrt{x+1}}}{\left({\sqrt{x}}-1\right)\left({\sqrt{x}}+1\right)}}\)

\(={\dfrac{\left({\sqrt{x}}-1\right)^{2}}{\left({\sqrt{x}}-1\right)\left({\sqrt{x}}+1\right)}}={\dfrac{{\sqrt{x}}-1}{\sqrt{x}+1}}\)

 

2. Cho biểu thức P = B : A. Tìm giá trị của x để P < 0.

Hướng dẫn:

P = B : A

\(\mathbf{P}={\dfrac{{\sqrt{\mathbf{x}}}-1}{{\sqrt{\mathbf{x}}}+1}}\ : {\dfrac{\mathbf{x}+3}{{\sqrt{\mathbf{x}}}+1}}\ = {\dfrac{{\sqrt{\mathbf{x}}}-1}{\mathbf{x}+3}}\)

P < 0 \(\Leftrightarrow \ \) \({\dfrac{{\sqrt{x}}-1}{x+3}}\lt 0\)

\(\Leftrightarrow \ \)\({\sqrt{\mathbf{x}}}-1\lt 0~{\mathrm{(Do~}}\mathbf{x}+3\gt 0)\)

\(\Leftrightarrow \ \)\({\sqrt{\mathbf{x}}} < 1\)

\(\Leftrightarrow \ \)x < 1

 

3. Tìm giá trị nhỏ nhất của \({\dfrac{1}{\mathrm{P}}}\) với x > 1

Hướng dẫn:

\({\dfrac{1}{\mathrm{P}}}=1:{\dfrac{{\sqrt{\mathrm{x}}}-1}{\mathrm{x}+3}}={\dfrac{\mathrm{x}+3}{{\sqrt{\mathrm{x}}}-1}}={\dfrac{\mathrm{x}-1+4}{{\sqrt{\mathrm{x}}}-1}}={\sqrt{\mathrm{x}}}+1+{\dfrac{4}{\sqrt{\mathrm{x}}-1}}\)

\(={\sqrt{x}}+1+{\dfrac{4}{\sqrt{x}-1}}\)

Vì x \(\geq1\Rightarrow{\sqrt{x}}-1\gt 0;{\frac{4}{\sqrt{x-1}}}\gt 0\)

Áp dụng Cosi ta có: \({\sqrt{\mathbf{x}}}-1+{\dfrac{4}{\sqrt{\mathbf{x}-1}}}+2\geq2{\sqrt{\left({\sqrt{\mathbf{x}}}-1\right)\left({\dfrac{4}{\sqrt{\mathbf{x}-1}}}\right)}}+2=6\)

Dấu "=" xảy ra khi \({\sqrt{x}}-1={\dfrac{4}{\sqrt{x-1}}}\)

\(\Leftrightarrow \ \)\(\left({\sqrt{\mathbf{x}}}-1\right)^{2}=4\Leftrightarrow{\sqrt{\mathbf{x}}}-1=2\,\left(\operatorname{Do}\,{\sqrt{\mathbf{x}}}-1\gt 0\right)\)

\(\Leftrightarrow \ \)\({\sqrt{\mathbf{x}}} = 3\)

\(\Leftrightarrow \ \)x = 9 (TM)

Vậy x = 9

 

 

 

Câu III. Cho hàm số \(\mathbf{y}=\left(\mathbf{m}-1\right)\mathbf{x}+2\mathbf{m}-3\left(\mathrm{d}\right)\left(\mathbf{m}\neq1\right)\)

1. Tìm m để (d) đi qua A (1;5). Vẽ đồ thì hàm số m tìm được.

Hướng dẫn:

Cho x = 0 => y = 3 => A (0;3) ∈ d

\(\mathbf{y}=0\Rightarrow\mathbf{x}=-{\dfrac{3}{2}}\Rightarrow\mathbf{B}\left(-{\dfrac{3}{2}};0\right)\) ∈ d

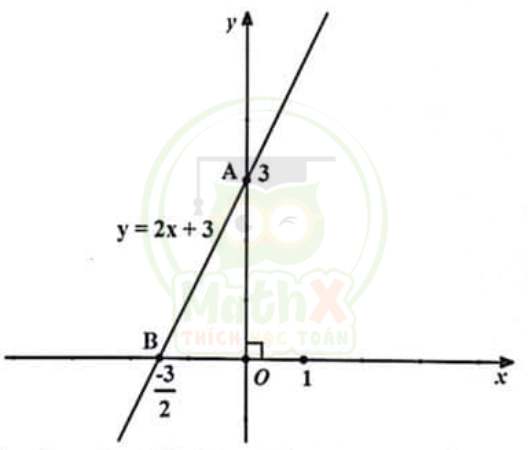
Vậy đồ thị hàm số y = 2x + 3 là đường thẳng d đi qua 2 điểm A,B.

 

2. Tìm m để (d) // (\(\mathbf{d}_{1}\)) : y = x + 3

Hướng dẫn:

(d) song song (\(\mathbf{d}_{1}\)) khi 

\(\begin{cases} {m-1 = 1} \\ {2m-3 ≠3}\end{cases}\) \(\Leftrightarrow \ \) \(\begin{cases} {m = 2} \\ {m ≠3}\end{cases}\)\(\Leftrightarrow \ \)m = 2

 

3. Chứng minh (d) luôn đi qua điểm cố định với mọi m.

Hướng dẫn:

Gọi M (\(\mathbf{x}_{0}\);\(\mathbf{y}_{0}\)) là điểm cố định mà (d) luôn đi qua \(\forall \)m

Khi đó phương trình \(\Leftrightarrow \ \)\(\mathbf{y}_{0}\) = (m - 1)\(\mathbf{x}_{0}\) + 2m - 3 luôn đúng \(\forall \)m

\(\Leftrightarrow \ \)\(\mathbf{y}_{0}\) = m\(\mathbf{x}_{0}\) - \(\mathbf{x}_{0}\) + 2m - 3 luôn đúng

\(\Leftrightarrow \ \)m (\(\mathbf{x}_{0}\) + 2) - \(\mathbf{x}_{0}\) - \(\mathbf{y}_{0}\) - 3 = 0 luôn đúng

\(\Leftrightarrow \ \)\(\begin{cases} {{x}_{0} + 2 = 0} \\ {-{y}_{0}-{x}_{0}-3=0}\end{cases}\) \(\Leftrightarrow \ \)\(\begin{cases} {{x}_{0} = -2} \\ {{y}_{0}=-{x}_{0}-3}\end{cases}\)\(\Leftrightarrow \ \)\(\begin{cases} {{x}_{0} = -2} \\ {{y}_{0}=-(-2})-3=-1\end{cases}\)\(\Leftrightarrow \ \)\(\begin{cases} {{x}_{0} = -2} \\ {{y}_{0}=-1}\end{cases}\)

Vậy M (-2;-1)

 

 

 

Câu IV.

1. Một cột đèn cao 9m. Ở một thời điểm trong ngày, mặt trời chiếu tạo thành bóng của cột đèn trên mặt đất là 5m. Hỏi lúc đó góc tạo bởi tỉa nắng mặt trời và mặt đất là bao nhiêu? (Làm tròn số đo góc tới độ)

Hướng dẫn:

Cột đèn AB, bóng AC tạo thành ∆ABC vuông tại A.

Gọi α = góc ACB là góc tạo bởi tia nắng mặt trời và mặt đất

Xét ∆ABC (góc A = \(90^{∘}\))

∆ = \({\dfrac{\mathrm{AB}}{\mathrm{AC}}}={\dfrac{9}{5}}\Rightarrow\alpha≈61^{o}\)

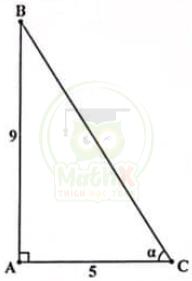
 \(\Leftrightarrow \ \) α \(= 61^{o}\)

 

2. Cho đường tròn (O; R). Dây MN khác đường kính. Qua O kẻ đường thẳng vuông góc với MN, cắt tiếp tuyến tại M của đường tròn ở điểm A.

a) AO giao với MN tại H. Chứng minh OH.OA = \(R^2\),

Hướng dẫn:

Vẽ hình đến câu a) được 0,25 điểm.

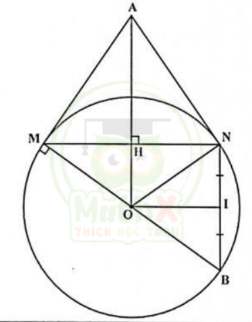
AM là tiếp tuyến của (O) => AM ⊥ OM => góc M = \(90^{∘}\)

Xét ∆AMO (góc M = \(90^{∘}\)), MH ⊥ OA, \({{MO^2}}\) = OH . OA (HTL)

Vì OM = R => OH . OA = \({R^2}\)

OH ⊥ MN => H là trung điểm của MN

=> AO là đường trung trực của MN

=> AM = AN

 

b) Chứng minh AN là tiếp tuyến của đường tròn (O; R).

Hướng dẫn:

Xét ∆MAO và ∆NAO có:

\(\begin{cases} AM=AN{} \\ {AO \ Chung \ \Rightarrow ∆MAO=∆NAO \ (c.c.c) } \\ {MO=NO} \end{cases}\)

=> góc N = góc M = \(90^{∘}\)

=> AN ⊥ ON

Mà N ∊ (O) => AN là tiếp tuyến của (O)

 

c) Kẻ đường kính MB. Gọi I là trung điểm của NB. Chứng minh bốn điểm O; H; N; I cũng thuộc một đường tròn.

Hướng dẫn:

I là trung điểm BN => OI ⊥ NB

Có ∆OIN vuông tại O nên nội tiếp đường tròn đường kính ON

Có ∆OHN vuông tại H nên nội tiếp đường tròn đường kính ON

=> O, I, N, H thuộc đường kính ON

 

d) Kéo dài OI cắt tỉa AN tại K. Qua O kẻ đường thẳng vuông góc với AB cắt tia MN tại Q. Chứng minh K là trung điểm của BQ.

Hướng dẫn:

Có góc HAP = góc CQP

∆AOC ~ ∆QOH (g.g)

=> AO.OH = OC.OQ

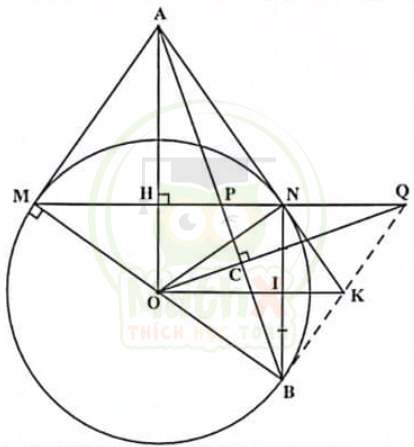
=> OC.OQ = \({R^2}\) = \({OB^2}\)

=> \(\dfrac{\mathrm{OC}}{\mathrm{OB}}\) = \(\dfrac{\mathrm{OB}}{\mathrm{OQ}}\)

∆OCB ~ ∆OBQ (c.g.c)

=> góc OBQ = OCB = \(90^{∘}\)

=> QB ⊥ MB

Lại có góc OBK = \(90^{∘}\) (= góc N)

=> KB ⊥ MB

=> B, K, Q thẳng hàng

∆BNQ có: I là trung điểm BN

IK // NQ

=> K là trung điểm BQ

 

 

 

Câu V. Cho hai số dương a; b thỏa mãn a + b \(\leq\) 4.

Tìm giá trị nhỏ nhất của biểu thức: \(P={\dfrac{1}{\mathbf{a}^{2}+\mathbf{b}^{2}}}+{\dfrac{25}{\mathbf{a}\mathbf{b}}}\)

Hướng dẫn:

Áp dụng BĐT \((\mathbf{a}+\mathbf{b})^{2}\geq4\mathbf{a}\mathbf{b}\Rightarrow{\dfrac{a+\mathbf{b}}{\mathbf{a}\mathbf{b}}}\geq{\dfrac{4}{\mathbf{a}+\mathbf{b}}}\Leftrightarrow{\dfrac{1}{a}}+{\dfrac{1}{\mathbf{b}}}\geq{\dfrac{4}{a+\mathbf{b}}}\)

Ta có P = \({\dfrac{1}{\mathbf{a}^{2}+\mathbf{b}^{2}}}+{\dfrac{25}{\mathbf{a}\mathbf{b}}}+\mathbf{a}\mathbf{b}={\dfrac{1}{\mathbf{a}^{2}+\mathbf{b}^{2}}}+{\dfrac{1}{2\mathbf{a}\mathbf{b}}}+{\dfrac{49}{2\mathbf{a}\mathbf{b}}}+\mathbf{a}\mathbf{b}\)

P ≥ \({\dfrac{4}{a^{2}+b^{2}+2a b}}+{\dfrac{49}{2a b}}+ab\) = \({\dfrac{4}{(a+1)^{2}}}+{\dfrac{49}{2ab}}+ab={\dfrac{4}{(a+1)^{2}}}+{\dfrac{17}{2ab}}+{\dfrac{16}{ab}}+ab\)

Lại có: \(2{\sqrt{\mathrm{ab}}}\leq\mathrm{a+b}\Rightarrow\mathrm{ab}\leq{\dfrac{(\mathrm{a}+\mathrm{b})^{2}}{4}}\leq{\dfrac{16}{4}}=4\)

\((\mathbf{a}+\mathbf{b})\leq4\Rightarrow(\mathbf{a}+\mathbf{b})^{2}\leq16\Rightarrow{\dfrac{4}{(\mathbf{a}+\mathbf{b})^{2}}}\geq{\dfrac{1}{4}}\)

Vì: \(\mathrm{ab}\leq4={\dfrac{17}{2\mathrm{ab}}}\,{\dfrac{17}{8}}\)

\({\dfrac{16}{a b}}+{\mathrm{ab}}\geq2{\sqrt{\dfrac{16}{\mathrm{ab}}}}\,a b=8\)

Vậy P ≥ \({\dfrac{1}{4}}+{\dfrac{17}{8}}+8={\dfrac{83}{8}}\)

Dấu "=" xảy ra khi 

\(\begin{cases} {a+b=4} \\ {a=b} \\ {ab=4} \end{cases}\)\(\Leftrightarrow \ \)a = b = 2

P nhỏ nhất bằng \(\dfrac{83}{8}\) khi a = b = 2

 

 

Trên đây MATHX đã hướng dẫn các em chữa đề thi học kì 1 môn toán lớp 9 THCS Marie Curie năm học 2023 - 2024

Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong TÀI LIỆU TOÁN LỚP 9 để có thể tích lũy thêm nhiều kiến thức và ôn tập hiệu quả hơn.

 

Phụ huynh và các em học có thể tham khảo một số tài liệu, đề thi lớp 9 ôn thi vào 10 khác tại đây:

TỔNG HỢP ĐỀ THI HỌC KÌ I LỚP 9 CỦA MỘT SỐ TRƯỜNG THCS CHẤT LƯỢNG CAO - MATHX

TUYỂN TẬP CÁC ĐỀ THI VÀO THPT 10 CHUYÊN

BỘ ĐỀ THI HSG TOÁN LỚP 9 CẤP TỈNH CÁC NĂM