Đề thi chuyên Tin sở GD Hà Nội năm 2024

Câu I.1 (2,0 điểm)

Giải phương trình:

\( \sqrt{x^2 - 3x} = x^2 - 3x - 2 \)

Câu I.2 (2,0 điểm)

Cho \( x, y, z \) là các số thực dương thỏa mãn:

\( \dfrac{x - 2y}{z} = \dfrac{y - 2z}{x} = \dfrac{z - 2x}{y} \)

Tính giá trị của biểu thức:

\( P = \left(2 + \dfrac{x}{y} \right) \left(2 + \dfrac{y}{z} \right) \left(2 + \dfrac{z}{x} \right) \)

Câu II.1 (2,0 điểm)

Tìm tất cả các số nguyên \( x, y \) thỏa mãn:

\( 2x^2 + 2xy + 3y = 4y^2 + 3 \)

Câu II.2 (2,0 điểm)

Cho các số nguyên dương \( x, y, z \) và số nguyên tố \( p \) thỏa mãn:

\( \dfrac{p}{2x + y} = \dfrac{x - y}{p} \)

Chứng minh \( p = 3y + 2 \)

Câu III.1 (2,0 điểm)

Cho \( a, b, c \) là các số nguyên dương thỏa mãn:

\( \dfrac{a - b^2}{b} = a(a - c^2) \)

Chứng minh: \( b = c \)

Câu III.2 (2,0 điểm)

Với \( a, b, c \) là các số thực không âm thỏa mãn:

\( a \leq 1, b \leq 1, c \leq 1 \) và \( a^2 + b^2 + c^2 = 2 \)

Tìm GTLN và GTNN của:

\( T = \dfrac{a^4}{bc + 2} + \dfrac{b^4}{ca + 2} + \dfrac{c^4}{ab + 2} \)

Câu IV (3,0 điểm)

Cho tam giác \( ABC \) với \( AB < AC \), nội tiếp đường tròn \( (O) \). Đường thẳng đi qua \( A \) và song song với \( BC \) cắt \( (O) \) tại điểm thứ hai là \( D \). Gọi \( M \) là trung điểm \( BC \), \( DM \cap (O) = S \).

1. Chứng minh \( \triangle ACS \sim \triangle BMS \)
2. Gọi \( J \) là trung điểm \( AS \), \( BJ \cap (O) = T \). Chứng minh: \( CT \parallel AS \)
3. Các đường \( DE, BF, CK \) của tam giác \( BCD \) đồng quy tại \( H \). Gọi \( L \) là chân đường vuông góc từ \( H \) xuống \( KF \). Chứng minh \( AE \cap DL \in (O) \)

Câu V (1,0 điểm)

Cho bảng ô vuông \( n \times n \) và hai loại miếng ghép “dấu cộng”, “dấu trừ” như hình dưới.

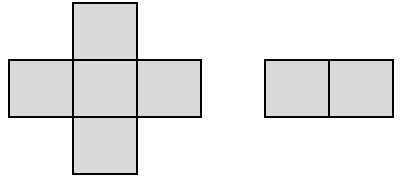
Các miếng không được chồng, có thể xoay 90 độ.

1. Chỉ ra cách phủ kín khi \( n = 6 \)
2. Tìm tất cả giá trị \( n \) để bảng phủ kín bởi hai loại miếng trên.