
Nhằm giúp các em học sinh ôn tập và chuẩn bị thật tốt cho kì thi học kì 2 sắp tới. Đội ngũ Mathx.vn biên soạn bộ 5 đề thi học kì 2 lớp 8 năm học 2024 - 2025 tài liệu có đáp án và lời giải chi tiết bám sát cấu trúc của các đầu sách trường, phòng, sở giáo dục trên cả nước.
Phụ huynh và các em học sinh xem thêm bộ 5 đề thi học kì 2 toán lớp 8 kèm lời giải chi tiết tại đây:
TỔNG HỢP ĐỀ THI HỌC KỲ 2 MÔN TOÁN LỚP 8 2024 KÈM LỜI GIẢI - ĐỀ 1
TỔNG HỢP ĐỀ THI HỌC KỲ 2 MÔN TOÁN LỚP 8 2024 KÈM LỜI GIẢI - ĐỀ 2
TỔNG HỢP ĐỀ THI HỌC KỲ 2 MÔN TOÁN LỚP 8 2024 KÈM LỜI GIẢI - ĐỀ 3
TỔNG HỢP ĐỀ THI HỌC KỲ 2 MÔN TOÁN LỚP 8 2024 KÈM LỜI GIẢI - ĐỀ 4
TỔNG HỢP ĐỀ THI HỌC KỲ 2 MÔN TOÁN LỚP 8 2024 KÈM LỜI GIẢI - ĐỀ 5
Câu 1 (2,5 điểm): Cho các biểu thức \(A={\dfrac{x-3}{x+2}}\) và \(B=\dfrac{6-7x}{x^{2}-4}+\dfrac{3}{x+2}-\dfrac{2}{2-x}\)
a) Tìm điều kiện xác định của B và rút gọn biểu thức B.
b) Cho \(A={\dfrac{1}{2}}\), khi đó hãy tính giá trị của B.
c) Đặt \(M={\dfrac{A}{B}}\) Tìm các giá trị của x để \(|M|=-M.\)
Lời giải:
a) Tìm điều kiện xác định của B và rút gọn biểu thức B.
Điều kiện xác định: \(\left\{ \begin{array}{} x-2 ≠0\\ x+2≠0 \\ \end{array} \right.\) => \(\left\{ \begin{array}{} x≠2\\ x≠-2 \\ \end{array} \right.\)
\(B=\dfrac{6-7x}{x^{2}-4}+\dfrac{3}{x+2}-\dfrac{2}{2-x}\)
\(={\dfrac{6-7x}{(x-2)\left(x+2\right)}}+{\dfrac{3}{x+2}}+{\dfrac{2}{x-2}}\)
\(=\displaystyle{\dfrac{6-7x+3\left(x-2\right)+2\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}}\)
\(={\dfrac{6-7x+3x-6+2x+4}{(x-2)\left(x+2\right)}}\)
\(={\dfrac{-2x+4}{\left(x-2\right)\left(x+2\right)}}\)
\(={\dfrac{-2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}}\)
\(={\dfrac{-2}{x+2}}\)
b) Cho \(A={\dfrac{1}{2}}\), khi đó hãy tính giá trị của B.
Điều kiện xác định: x ≠ ± 2
.
Theo câu a) ta có: \(A={\dfrac{x-3}{x+2}}\)
Ta có:
\(A={\dfrac{1}{2}}\Leftrightarrow{\dfrac{x-3}{x+2}}={\dfrac{1}{2}}\)
\(\Rightarrow2x-6=x+2\)
\(\Leftrightarrow2x-x=2+6\)
\(\Leftrightarrow x=8\ \ (t m)\)
Thay x = 8 vào B ta được:
\(B={\dfrac{-2}{8+2}}={\dfrac{-2}{10}}={\dfrac{-1}{5}}.\)
c) Đặt \(M={\dfrac{A}{B}}\) Tìm các giá trị của x để \(|M|=-M.\)
Điều kiện xác định: x ≠ ± 2
\(M={\dfrac{A}{B}}={\dfrac{{\dfrac{x-3}{x+2}}}{{\dfrac{-2}{x+2}}}}={\dfrac{x-3}{-2}}\)
\(|M|=-M\Rightarrow M\lt 0\Leftrightarrow\dfrac{x-3}{-2}\lt 0\Rightarrow x-3\gt 0\leftrightarrow x\gt 3.\)
Kết hợp điều kiện x ≠ ± 2 > 3
Vậy |M| = -M khi x > 3
Câu 2 (2,0 điểm): Giải bài toán sau bằng cách lập phương trình:
Một xe máy và một ô tô cùng khởi hành từ tỉnh A đi đến tỉnh B. Xe máy đi với vận tốc 30km/h, ô tô đi với vận tốc 40km/h. Sau khi đi được nửa quãng đường AB, ô tô tăng vận tốc thêm 5km/h trên quãng đường còn lại, do đó nó đến tỉnh B sớm hơn xe máy 1 giờ 10 phút. Tính độ dài quãng đường AB.
Lời giải:
Đổi 1 giờ 10 phút = \(\dfrac{7}{6}\)
Gọi quãng đường AB dài x (km),(x > 0).
Thời gian xe máy đi hết quãng đường AB là \(\dfrac{x}{30}\) (giờ)
Thời gian ô tô đi nửa đầu quãng đường AB là \({\dfrac{x}{2}}:40={\dfrac{x}{80}}\) (giờ)
Thời gian ô tô đi nửa sau quãng đường AB là \({\dfrac{x}{2}}:(40+5)={\dfrac{x}{90}}\) (giờ)
Do ô tô đến tỉnh B sớm hơn xe máy 1 giờ 10 phút nên ta có phương trình:
\({\dfrac{x}{30}}={\dfrac{7}{6}}+{\dfrac{x}{80}}+{\dfrac{x}{90}}\)
\(\Leftrightarrow{\dfrac{24x}{720}}={\dfrac{840}{720}}+{\dfrac{9x}{720}}+{\dfrac{8x}{720}}\)
\(\Leftrightarrow24x=840+9x+8x\)
\(\Leftrightarrow24x-9x-8x=840\)
\(\Leftrightarrow\ 7 x=840\)
\(\Leftrightarrow x=120\;\;\;(t m)\)
Vậy quãng đường AB dài 120km.
Câu 3 (1,5 điểm): Giải các phương trình sau:
a) \((2x-1)\left(x+5\right)=2\left(x^{2}+{\dfrac{3}{2}}\right)-7x\)
b) \(x^{2}-7x+12=0\)
c) \({\dfrac{4x^{2}}{x^{2}-3x+2}}-{\dfrac{x-5}{x-1}}+{\dfrac{2x-1}{2-x}}=0\)
Lời giải:
a) \((2x-1)\left(x+5\right)=2\left(x^{2}+{\dfrac{3}{2}}\right)-7x\)
\(\Leftrightarrow2x^{2}+10x-x-5=2x^{2}+3-7x\)
\(\Leftrightarrow2x^{2}+10x-x-2x^{2}+7x=3+5\)
\(\Leftrightarrow16x=8\)
\(\Leftrightarrow x={\dfrac{1}{2}}\)
Vậy tập nghiệm của phương trình là: \(S=\left\{{\dfrac{1}{2}}\right\}\)
b) \(x^{2}-7x+12=0\)
\(\Leftrightarrow x^{2}-4x-3x+12=0\)
\(\Leftrightarrow x\left(x-4\right)-3\left(x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(x-3\right)=0\)
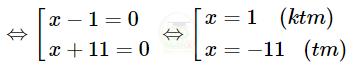
Vậy tập nghiệm của phương trình là: \(S=\{-11\}\,.\)
Câu 4 (3,5 điểm): Cho hình chữ nhật ABCD có AB = 8cm,BC = 6cm.. Kẻ BH vuông góc với AC tại H,DM vuông góc với AC tại M.
a) Chứng minh ΔABH đồng dạng với ΔACB và suy ra \(A C.\,A H=A B^{2}.\)
b) Tính độ dài các đoạn thẳng \(A C,\ B H,\ C H.\)
c) Gọi I là điểm đối xứng với B qua AC. Chứng minh DM = IH và ACID là hình thang cân.
d) Gọi E,F lần lượt là trung điểm của AH,CD và K là giao điểm của BF với AC.
Chứng minh \(B F.E K\geq B E.E F.\)
Lời giải:
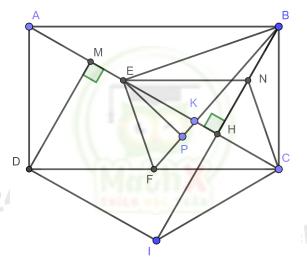
a) Xét ΔABH và ΔACB có:
\(\angle H=\angle B\left(=90^{0}\right)\)
∠BAH chung
\(\Rightarrow\Delta A B H\sim\Delta A C B\ \ (g-g)\,.\)
\(\Rightarrow{\dfrac{A B}{A H}}={\dfrac{A C}{A B}}\Rightarrow A C.A H=A B^{2}.\)
b) Tính độ dài các đoạn thẳng \(A C,\ B H,\ C H.\)
Áp dụng định lý Pytago cho tam giác vuông ABC vuông tại B có:
\(A C^{2}=A B^{2}+B C^{2}=8^{2}+6^{2}=100\Rightarrow A C=10~c m\)
Theo câu b) ta có: \(A C.\,A H=A B^{2}\Rightarrow10.AH=8^{2}\)
\(\Rightarrow A H={\dfrac{64}{10}}=6,4\ c m.\)
Áp dụng định lý Pytago cho tam giác vuông ABH vuông tại H có:
\(A B^{2}=A H^{2}+B H^{2}\Rightarrow B H=\sqrt{8^{2}-6,4^{2}}=4,8c m\)
Từ đó \(C H=A C-A H=10-6,4=3,6c m\)
c) Gọi I là điểm đối xứng với B qua AC. Chứng minh DM = IH và ACID là hình thang cân.
Vì I là điểm đối xứng với B qua AC nên AC là đường trung trực của BI
\(\left\{ \begin{array}{} BI⊥AC \\ HB=HI \\ \end{array} \right.\)
Vì ABCD là hình chữ nhật nên AB//CD
\(\Rightarrow\angle B A H=\angle D C M\) (so le trong)
Xét ΔABH và ΔCDM có:
\(\angle A H B=\angle C M D\ \ (=90^{0})\)
AB = CD
\(\angle B A H=\angle D C M\ \ (c m t)\)
\(\Rightarrow\Delta A B H=\Delta C D M \ (c h-g n)\)
=> BH = DM (hai cạnh tương ứng)
Mà BH = IH (cmt) \(\Rightarrow D M=I H\left(=B H\right)\)
Ta có: \(\left\{ \begin{array}{} IH⊥AC \\ DM=AC\\ \end{array} \right.\) => IH // DM
Mà IH = DM => DMHI là hình bình hành (dhnb).
\(\Rightarrow I D//M H\Rightarrow I D//A C\)
⇒ ACID là hình thang (1)
Xét ΔBCH và ΔICH có:
CH cạnh chung
\(\angle C H B=\angle C H\) (do BI⊥CH)
BH = IH (cmt)
Nên \(\Delta B C H=\Delta I C H\ \ (c-g-c)\)
=> BC = CI
Mà BC = AD (do ABCD là hình chữ nhật)
⇒ AD = CI
Xét ΔADM và ΔCIH có:
\(\angle A M D=\angle C H\left(=90^{0}\right)\)
AD = CI (cmt)
DM = IH (cmt)
⇒ ΔADM = ΔCIH (ch−cgv)
\(\Rightarrow\angle D A M=\angle I C H\ (2)\)
Từ (1), (2)
⇒ ACID là hình thang cân. (đpcm)
d) Gọi E,F lần lượt là trung điểm của AH,CD và K là giao điểm của BF với AC.
Chứng minh \(B F.E K\geq B E.E F.\)
Gọi N là trung điểm BH ⇒ EN là đường trung bình của ΔABH
\(\left\{ \begin{array}{} EN//AB \\ EN = \textstyle{\dfrac{A B}{2}} \end{array} \right.\)
Mà \(\left\{ \begin{array}{} FC//AB \\ F C={\dfrac{C D}{2}}={\dfrac{A B}{2}} \end{array} \right.\) => \(\left\{ \begin{array}{} FC//EN\\ FC= NE \end{array} \right.\) => ENCF là hình bình hành (dhnb)
=> EF // NC (1)
Ta có: \(\left\{ \begin{array}{} AB//EN \\ AB⊥BC\\ \end{array} \right.\) => EN ⊥ BC
Lại có: BH ⊥ EC => N là trực tâm tam giác BEC => NC ⊥ EB (2)
Từ (1), (2) => EF ⊥ EB => ΔBEF vuông tại E.
Gọi \(E P\perp B F\left(P\in B F\right)\) mà \(K\in B F\Rightarrow E K\geq E P\)
\(S_{\Delta B E F}=\dfrac{1}{2}B E.E F=\dfrac{1}{2}E P.B F\)
\(\Rightarrow B E.E F=E P.B F\leq E K.B F\)
=> BE.EF ≤ BF.EK (đpcm)
Câu 5 (0,5 điểm): Tìm m để hai bất phương trình sau có cùng tập nghiệm:
\(x^{2}\left(x-5\right)\gt 4-5x\) và \(m x-5\gt x-2m.\)
Lời giải:
\(x^{2}\left(x-5\right)\gt 4-5x\)
\(\Leftrightarrow x^{3}-5x^{2}\gt 4-5x\)
\(\Leftrightarrow x^{3}-5x^{2}+5x-4\gt 0\)
\(\Leftrightarrow x^{3}-4x^{2}-x^{2}+4x+x-4\gt 0\)
\(\Leftrightarrow x^{2}\left(x-4\right)-x\left(x-4\right)+\left(x-4\right)\gt 0\)
\(\Leftrightarrow\left(x-4\right)\left(x^{2}-x+1\right)\gt 0\)
Vì \(x^{2}-x+1\!\!=\!x^{2}-2\!\cdot\!{x}.\,{\dfrac{1}{2}}+{\dfrac{1}{4}}+{\dfrac{3}{4}}\)
\(=\left(x-{\dfrac{1}{2}}\right)^{2}+{\dfrac{3}{4}}\geq{\dfrac{3}{4}}\gt 0\) với mọi x
\(\Rightarrow x-4\gt 0\Longleftrightarrow x\gt 4\)
Lại có:
\(m x-5\gt x-2m\)
\(\Leftrightarrow m x-x\gt 5-2m\)
\(\Leftrightarrow(m-1)\,x\gt 5-2m\)
TH1: \(m-1=0\Leftrightarrow m=1\Rightarrow0x\gt 5-2.1=3\) (vô lý)
TH2: \(m-1\neq0\Leftrightarrow m\neq1\)
Để hai bất phương trình đã cho có cùng tập nghiệm x > 4 thì
\(m-1\gt 0\Leftrightarrow m\gt 1\Rightarrow x\gt {\dfrac{5-2m}{m-1}}\) và \({\dfrac{5-2m}{m-1}}=4\)
\(\Rightarrow5-2m=4m-4\)
\(\Leftrightarrow-6m=-9\)
\(\Leftrightarrow m=\dfrac{3}{2}\ \left(t m\right)\)
Với \(\Leftrightarrow m=\dfrac{3}{2}\ \)thì hai bất phương trình có cùng tập nghiệm.
Trên đây MATHX đã hướng dẫn các em giải chi tiết đề thi học kì 2 môn toán lớp 8 - đề số 1. Ngoài ra các bậc phụ huynh cần cho con em mình học đúng phương pháp và tham khảo các khóa học online tại MATHX.VN để giúp con tự tin chinh phục môn toán nhé.