Trường Toán Online MATHX
MATHX.VN biên soạn bộ đề kiểm tra giữa kì 2 Toán 7 năm 2023 kèm lời giải chi tiết giúp các em học sinh nhanh chóng làm quen với cấu trúc đề thi, ôn tập để đạt được kết quả cao trong kì thi giữa học kì sắp tới. Mời các em cùng tham khảo dưới đây!
Phụ huynh và các em học sinh xem thêm đề thi giữa kì 2 môn toán lớp 7 năm học 2023 - 2024 tại đây:
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 1
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 2
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 3
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 4
TỔNG HỢP ĐỀ THI GIỮA KỲ 2 MÔN TOÁN LỚP 7 2023 - 2024 KÈM LỜI GIẢI - ĐỀ 5
Câu 7. Cho tam giác ABC, đường trung tuyến AM = 9 cm. Gọi G là trọng tâm của tam giác. Tính độ dài GM?
Bài 1. Tìm x biết:
a) \({\dfrac{1}{12}}+x={\dfrac{-11}{12}}\)
b) \({\dfrac{2x-1}{27}}={\dfrac{3}{2x-1}}\)
Lời giải:
a) \({\dfrac{1}{12}}+x={\dfrac{-11}{12}}\)
\(x={\dfrac{-11}{12}}-{\dfrac{1}{12}}\)
\(x={\dfrac{-11-1}{12}}\)
\(x={\dfrac{-12}{12}}=-1\)
Vậy \(x = -1\)
b) \({\dfrac{2x-1}{27}}={\dfrac{3}{2x-1}}\)
\((2x-1)^{2}=27.3=81\)
\((2x-1)^{2}=(\pm9)^{2}\)
Trường hợp 1:
2x - 1 = 9
2x = 10
x = 5
Trường hợp 2:
2x - 1 = -9
2x = -8
x = -4
Vậy x ∈ {5; - 4}
Bài 2. Ba đội công nhân tham gia làm đường và phải làm ba khối lượng công việc như nhau. Để hoàn thành công việc, đội I cần 4 ngày, đội II cần 6 ngày và đội III cần 8 ngày. Tính số công nhân của mỗi đội, biết rằng đội I có nhiều hơn đội II là 4 người (năng suất mỗi người như nhau).
Lời giải:
Gọi số công nhân của 3 đội lần lượt là x,y,z (điều kiện x,y,z ∈ N*)
Vì đội I có nhiều hơn đội II là 4 người nên: x − y = 4
Vì số năng suất mỗi người là như sau, nên số người và số ngày hoàn thành công việc là hai đại lượng tỉ lệ nghịch, nên ta có:
4x = 6y = 8z hay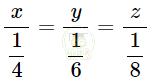 
Theo tính chất của dãy tỉ số bằng nhau, ta có:
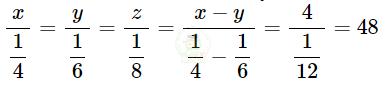
Vậy số công nhân của 3 đội lần lượt là: 12 công nhân, 8 công nhân, 6 công nhân.
Bài 3. Cho các đa thức:
\(A\left(x\right)=2\,x^{4}-5\,x^{3}+7\,x-5+4\,x^{3}+3\,x^{2}+2\,x+3\)
\(B\left(x\right)=5\,x^{4}-3\,x^{3}+5\,x-3\,x^{4}-2\,x^{3}\,+9-6\,x\)
\(C\left(x\right)=x^{4}+4\,x^{2}+5\)
a) Thu gọn và sắp xếp các hạng tử của đa thức A (x), B (x) theo lũy thừa giảm dần của biến.
b) Tính \(A\left(x\right)+B\left(x\right);\,A\left(x\right)-B\left(x\right).\)
c) Chứng minh rằng đa thức C (x) không có nghiệm
Lời giải:
a) Thu gọn:
\(A\left(x\right)=2\,x^{4}-5\,x^{3}+7\,x-5+4\,x^{3}+3\,x^{2}+2\,x+3\)
\(A\left(x\right)=2\,x^{4}+\left(-5\,x^{3}+4\,x^{3}\right)+3x^{2}+\left(7\,x+2\,x\right)-5+3\)
\(A\left(x\right)=2\,x^{4}-x^{3}+3\,x^{2}+9\,x\,-2\)
\(B\left(x\right)=5\,x^{4}-3\,x^{3}+5\,x-3\,x^{4}-2\,x^{3}\,+9-6\,x\)
\(B\left(x\right)=\left(5\,x^{4}-3\,x^{4}\right)+\left(-3\,x^{3}-2\,x^{3}\right)+\left(5\,x-6\,x\right)+9\)
\(\begin{array}{r l}{B\left(x\right)={}}&{{}2\,x^{4}\,-\,5x^{3}-x+9}\end{array}\)
b) Tính \(A\left(x\right)+B\left(x\right);\,A\left(x\right)-B\left(x\right).\)
+) \(A\left(x\right)+B\left(x\right)=\left(2\,x^{4}-x^{3}+3\,x^{2}+9\,x-2\right)\)
+) \(\left(2\,x^{4}-5\,x^{3}-x+9\right)\)
\(=(2\,x^{4}+2\,x^{4})+(-x^{3}-5\,x^{3})+3\,x^{2}+(9\,x-x)+(-2+9)\)
\(\,=\ \ 4\,x^{4}-6\,x^{3}+3\,x^{2}+8\,x+7\)
+) \(A\left(x\right)-B\left(x\right)=\left(2\,x^{4}-x^{3}+3\,x^{2}+9\,x-2\right)\)
\(-\ \left(2\,x^{4}-5\,x^{3}-x+9\right)\)
\(=(2\,x^{4}-\,x^{3}+3\,x^{2}+9\,x-2)-2\,x^{4}+5\,x^{3}+x-9\,\)
\(=(2\,x^{4}-\,2\,x^{4})+\left(-x^{3}+5\,x^{3}\right)+3\,x^{2}+(9\,x+x) + (-2-9)\)
\(\begin{array}{r l}{={}}&{{}\,4\,x^{3}+3\,x^{2}+10x-11}\end{array}\)
c) Chứng minh rằng đa thức C (x) không có nghiệm.
Ta có: \(C\left(x\right)=x^{4}+4\,x^{2}+5.\)
Vì \(x^{4}\;\gt 0,\;\forall x\;\mathrm{và}\;x^{2}\gt 0,\;\forall x\) nên C (x) > 0, ∀x.
=> không có giá trị nào của x làm cho C (x) = 0.
=> C (x) là đa thức không có nghiệm.
Bài 4. Cho ΔABC vuông tại A có ∠C = 30°, đường cao AH. Trên đoạn HC lấy điểm D sao cho HD = HB.
a) Chứng minh ΔAHB = ΔAHD.
b) Chứng minh ΔABD là tam giác đều.
c) Từ C kẻ CE vuông góc với đường thẳng AD (E ∈ AD). Chứng minh DE = HB
d) Từ D kẻ DF vuông góc với AC (F thuộc AC), I là giao điểm của CE và AH. Chứng minh ba điểm I, D, F thẳng hàng.
Lời giải:
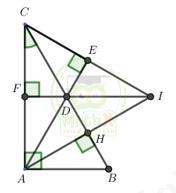
a) Xét ΔAHB và ΔAHD ta có:
HD = HB (gt)
AH chung
∠AHB = ∠AHD = 90°
=> ΔAHB = ΔAHD (c.g.c)
b) ΔABC vuông tại A.
có ∠C = 30° => ∠B = 90° - 30° = 60° (định lý tổng ba góc của một tam giác).
Vì ΔAHB = ΔAHD (cmt)
=> AB = AD (hai cạnh tương ứng).
=> ΔABD cân tại A mà ∠B = 60°
Do đó: ΔABD là tam giác đều.
c) Vì ΔABD là tam giác đều (cmt)
=> ∠DAB = 60°
=> ∠CAD = 90° - ∠DAB
= 90° - 60° = 30°
Xét ΔACD có ∠ACD = ∠CAD = 30°
=> ΔACD cân tại D.
=> CD = AD
Xét ΔDEC và ΔDAH có:
CD = AD (cmt)
∠E = ∠H = 90°
∠CDE = ∠ADH (đối đỉnh)
=> ΔDEC = ΔDHA (cạnh huyền – góc nhọn).
=> DE = DH (hai cạnh tương ứng).
Mà DH = DB (giả thiết)
=> DE = DB.
d) Từ D kẻ DF vuông góc với AC (F thuộc AC), I là giao điểm của CE và AH. Chứng minh ba điểm I, D, F thẳng hàng.
Ta có:
DF ⊥ AC (gt)
AB ⊥ AC (gt)
=> DF // AD (1)
Ta lại có:
∠FDC = ∠HDI (đối đỉnh)
Mà: ∠FDC = 90° - ∠C = 90° - 30° = 60°
=> ∠FDC = ∠HDI = 60°
Mà ∠B = 60°
=> ∠B = ∠DHI
Mà hai góc này ở vị trí so le trong
Do đó: DI // AB (2)
Từ (1) và (2), suy ra: ∠I,D,B là ba điểm thẳng hàng.
Bài 5. Cho a,b,c là các số thực khác không (b ≠ c) và \({\dfrac{1}{c}}={\dfrac{1}{2}}\left({\dfrac{1}{a}}+{\dfrac{1}{b}}\right)\). Chứng minh rằng: \({\dfrac{a}{b}}={\dfrac{a-c}{c-b}}.\)
Lời giải:
Ta có: \({\dfrac{1}{c}}={\dfrac{1}{2}}\left({\dfrac{1}{a}}+{\dfrac{1}{b}}\right)\)
\(\Rightarrow{\dfrac{1}{c}}={\dfrac{a+b}{2a b}}\)
=> 2ab = ac + bc
=> ab + ab = ac + bc
=> bc - bc = ac - ab
=> b (a - c) = a (c - b)
=> \({\dfrac{a}{b}}={\dfrac{a-c}{c-b}}\) (đpcm)
Trên đây MATHX đã hướng dẫn các em giải đề thi giữa kì 2 môn toán lớp 7 năm học 2023 - 2024 - đề 1. Ngoài ra các bậc phụ huynh cần cho con em mình học đúng phương pháp và tham khảo các khóa học online tại MATHX.VN để giúp con tự tin chinh phục môn toán nhé.
