
Kì thi học kì 1 các trường và tỉnh thành khu vực Hà Nội vừa kết thúc, nhiều em học sinh và phụ huynh đang hướng về nguồn thông tin hữu ích để tự ôn tập và nắm vững kiến thức. Bài viết này MATHX biên soạn gửi tới phụ huynh và các em hướng dẫn giải chi tiết đề thi học kì 1 môn toán lớp 9 quận Ba Đình năm học 2023 - 024. Các em học sinh tải để về làm trước sau đó so sánh kết quả và cách giải chi tiết trong bài viết này. Chúc các em học tập tốt!
Thời gian làm bài: 90 phút
Ngày kiểm tra: 20/12/2023
Bài I: (2,0 điểm)
1) Tính giá trị của biểu thức: \(K={\dfrac{2}{\sqrt{3}-1}}-\sqrt{27}+\left(\sqrt{3}+1\right)^{2}.\)
2) Giải phương trình: \({\sqrt{x^{2}-4x+4}}-2x=5.\)
Hướng dẫn:
1).
\(K={\dfrac{2}{\sqrt{3}-1}}-\sqrt{27}+\left(\sqrt{3}+1\right)^{2}\)
\(=\dfrac{2\Bigl(\sqrt{3}+1\Bigr)}{\Bigl(\sqrt{3}-1\Bigr)\Bigl(\sqrt{3}+1\Bigr)}-3\sqrt{3}+3+2\sqrt{3}+1\)
\(={\dfrac{2\left({\sqrt{3}}+1\right)}{3-1}}+4-{\sqrt{3}}\)
\(=\sqrt{3}+1+4-\sqrt{3}=5.\)
2). Giải phương trình: \({\sqrt{x^{2}-4x+4}}-2x=5.\) (1)
(1) ⇔ \({\sqrt{\left(x-2\right)^{2}}}=2x+5\Leftrightarrow\left|x-2\right|=2x+5\)
Nếu \(x-2\geq0:\left(1\right)\Leftrightarrow x-2=2x+5\Leftrightarrow x=-7\) (KTM)
Nếu \(x-2\lt 0:(1)\Leftrightarrow2-x=2x+5\Leftrightarrow x=-1\) (TM)
Vậy phương trình (1) có tập nghiệm là S = {-1}.
Bài II: (2,0 điểm)
Cho hai biểu thức \(A={\dfrac{\sqrt{x}-5}{\sqrt{x}+2}}\) và \(B=\dfrac{\sqrt{x}}{\sqrt{x}+4}-\dfrac{2}{\sqrt{x}-4}-\dfrac{4\sqrt{x}}{16-x}\) với x ≥ 0 ; x ≠ 16.
1) Tính giá trị của biểu thức A khi x = 4.
2) Chứng minh \(A={\dfrac{\sqrt{x}+2}{\sqrt{x}+4}}\)
3) Tìm x để biểu thức Q = A.B nhận giá trị nguyên.
Hướng dẫn:
1) \(A={\dfrac{\sqrt{x}-5}{\sqrt{x}+2}}\) với x ≥ 0 ; x ≠ 16.
Thay x = 4 (thỏa mãn điều kiện) vào biểu thức A ta được:
\(A={\dfrac{\sqrt{4}-5}{\sqrt{4}+2}}={\dfrac{2-5}{2+2}}=-{\dfrac{3}{4}}\)
Vậy A = \(-{\dfrac{3}{4}}\) khi x = 4.
2) \(B=\dfrac{\sqrt x}{\sqrt{x}+4}-\dfrac{2}{\sqrt{x}-4}-\dfrac{4\sqrt{x}}{16-x}\) với x ≥ 0 ; x ≠ 16.
\(B=\dfrac{\sqrt{x}(\sqrt{x}-4)-2(\sqrt{x}+4)+4\sqrt{x}}{(\sqrt{x}-4)(\sqrt{x}+4)}\)
\(B=\dfrac{x-2\sqrt{x}-8}{(\sqrt{x}-4)(\sqrt{x}+4)}\)
\(B=\dfrac{(\sqrt{x}-4)(\sqrt{x}+2)}{(\sqrt{x}-4)(\sqrt{x}+4)}\)
\(B=\dfrac{\sqrt{x}+2}{\sqrt{x}+4}\)
3) Ta có Q = A.B \(={\dfrac{\sqrt{x}-5}{\sqrt{x}+2}}\cdot{\dfrac{\sqrt{x}+2}{\sqrt{x}+4}}={\dfrac{\sqrt{x}-5}{\sqrt{x}+4}}=1-{\dfrac{9}{\sqrt{x}+4}}\)
x ≥ 0 \(\Leftrightarrow{\sqrt{x}}\geq0\Longleftrightarrow{\sqrt{x}}+4\geq4\Leftrightarrow{\dfrac{9}{{\sqrt{x}}+4}}\leq{\dfrac{9}{4}}\Leftrightarrow1-{\dfrac{9}{{\sqrt{x}}+4}}\geq1-{\dfrac{9}{4}}\)
\(\Leftrightarrow Q\geq-{\dfrac{5}{4}}.\)
\({\dfrac{9}{\sqrt{x+4}}}\gt 0\Rightarrow Q\lt 1\Rightarrow-{\dfrac{5}{4}}\leq Q\lt 1.\)
Q nguyên \(\Leftrightarrow Q\in\{-1;0\}\Rightarrow x\in\left\{{\dfrac{1}{4}};25\right\}.\)
Bài III: (2,0 điểm)
Cho hàm số: y = (m -1) x + 2 (m là tham số và m ≠ 1) có đồ thị là đường thẳng (d).
1) Tìm m để đường thẳng d song song với đường thẳng y = 2x – 1. Vẽ đồ thị hàm số với giá trị m vừa tìm được.
2) Tìm m để đường thẳng d cắt đường thẳng y = - 3x + 4 tại điểm I nằm bên phải trục tung.
Hướng dẫn:
1) Tìm m để đường thẳng d song song với đường thẳng y = 2x – 1.
(d) / / (\(d_1\)) : \(y=2x-1\) \(\begin{cases} {m-1=2} \\ {2≠1} \end{cases}\) ⇔ m = 3.
Khi đó (d) : y = 2x + 2. Vẽ đúng (d)
2) Tìm m để đường thẳng d cắt đường thẳng y = - 3x + 4 tại điểm I nằm bên phải trục tung.
(d) cắt (\(d_2\)) : y = - 3x + 4 ⇔ \(m-1\neq-3\Leftrightarrow m\neq-2.\)
Phương trình hoành độ giao điểm của (d) và (\(d_2\)):
\(\left(m-1\right)x+2=-3x+4\Leftrightarrow\left(m+2\right)x=2\Leftrightarrow x={\dfrac{2}{m+2}}.\)
d) cắt (\(d_2\)) tại điểm I có hoành độ \(x_{1}={\dfrac{2}{m+2}}.\)
I nằm bên phải trục tung
\(\Leftrightarrow x_{1}\gt 0\Leftrightarrow\frac{2}{m+2}\gt 0\Leftrightarrow m+2\gt 0\Leftrightarrow m\gt -2\)
Bài IV: (3,5 điểm)
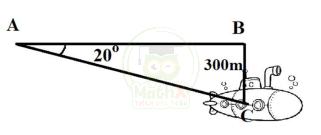
1) Một chiếc tàu ngầm đang ở trên mặt biển bắt đầu lặn xuống và di chuyển theo đường thẳng tạo với mặt nước một góc 20°. Một lúc sau, tàu ở độ sâu 300m so với mặt biển. Hỏi tàu đã di chuyển bao nhiêu mét (làm tròn đến chữ số hàng đơn vị).
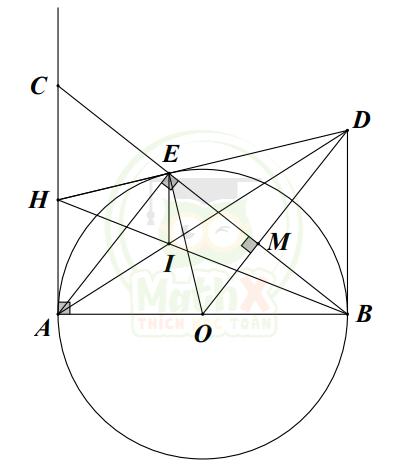
2) Cho đường tròn (O) tâm O đường kính AB. Trên tiếp tuyến tại A của (O) lấy điểm C. Gọi E là giao điểm của CB với (O). Từ O kẻ đường thẳng song song với AE, cắt BC tại M.
a) Chứng minh \({C{A^2}}\) = CE.CB.
b) Chứng minh bốn điểm A,C,O,M cùng thuộc một đường tròn.
c) Tiếp tuyến tại E của đường tròn (O) cắt OM tại D và cắt AC tại H; BH cắt AD tại I. Chứng minh DB là tiếp tuyến của (O) và EI vuông góc với AB.
Hướng dẫn:
1)

Tam giác ABC vuông tại B nên \(\sin A={\dfrac{B C}{A C}}\)
\(A C={\dfrac{B C}{\sin A}}={\dfrac{300}{\sin20^{\circ}}}\)
\(A C\approx877\left(m\right)\)
Vậy tàu ngầm đã di chuyển được khoảng 877 (m).
2) Vẽ hình đúng hết ý a
a) Chỉ ra tam giác ABC vuông tại A.
Chỉ ra AE ⊥ BC
Suy ra \({C{A^2}}\) = CE.CB. (hệ thức lượng trong tam giác vuông)
b) Chỉ ra tam giác OMC vuông tại M.
Nên tam giác OMC nội tiếp đường tròn đường kính OC (1)
Chỉ ra tam giác OAC nội tiếp đường tròn đường kính OC (2) Từ (1) và (2) suy ra bốn điểm A,C,O,M cùng thuộc một đường tròn đường kính OC.
c) +) Chứng minh được ∆EOD = ∆BOD (c.g.c)
Suy ra DB là tiếp tuyến của (O).
+) Theo tính chất hai tiếp tuyến cắt nhau ta có:
AH = EH, DE = DB
Vì AB ⊥ BD VÀ AB ⊥ AH nên BD // AH
Suy ra \({\dfrac{A H}{B D}}={\dfrac{H I}{I B}}\) (định lý Ta-lét)
Mà AH = EH, DE = DB
Nên \({\dfrac{E H}{E D}}={\dfrac{H I}{I B}}\)
Suy ra EI // BD (định lý Ta-lét đảo)
Mà AB ⊥ BD
Suy ra EI vuông góc với AB .
Bài V: (0,5 điểm)
Cho các số thực x y, thỏa mãn: \(x^{4}+y^{4}-3=2y^{2}(1-x^{2}).\)
Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức \(T=x^{2}+y^{2}.\)
Hướng dẫn:
\(x^{4}+y^{4}-3=2y^{2}(1-x^{2})\Leftrightarrow\left(x^{2}+y^{2}\right)^{2}=3+2y^{2}\geq3\)
\(\Leftrightarrow x^{2}+y^{2}\geq\sqrt{3}.\)
\(x^{4}+y^{4}-3=2y^{2}(1-x^{2})\Leftrightarrow\left(x^{2}+y^{2}\right)^{2}-2\left(x^{2}+y^{2}\right)-3=-2x^{2}\leq0\)
\(\Leftrightarrow\left(x^{2}+y^{2}+1\right)\!_{*}\!\left(x^{2}+y^{2}-3\right)\leq0\Leftrightarrow x^{2}+y^{2}\leq3.\)
Vậy GTNN của T là \(\sqrt{3}\) khi \(y=0;x^{2}={\sqrt{3}}\) ; GTLN của T là 3 khi \(x=0;y^{2}={3}.\)
Trên đây MATHX đã hướng dẫn các em chữa đề thi học kì 1 môn toán lớp 9 quận Ba Đình năm học 2023 - 2024.
Ngoài ra các em có thể tham khảo thêm các chuyên đề và tài liệu trong TÀI LIỆU TOÁN LỚP 9 để có thể tích lũy thêm nhiều kiến thức và ôn tập hiệu quả hơn.
Phụ huynh và các em tham khảo thêm một số tài liệu đề thi quận Ba Đình qua các năm tại đây:
ĐỀ KHẢO SÁT CHẤT LƯỢNG TOÁN 9 NĂM HỌC 2022-2023 QUẬN BA ĐÌNH - HÀ NỘI
ĐỀ KIỂM TRA GIỮA HỌC II TOÁN 9 TRƯỜNG THCS BA ĐÌNH NĂM HỌC 2022-2023
ĐỀ KIỂM TRA HỌC KÌ 1 LỚP 9 QUẬN BA ĐÌNH NĂM HỌC 2017 - 2018