
Thầy/cô MATHX xin gửi đến các em học sinh một số bài toán có nội dung hình học lớp 4. Hình học luôn là một trong những nội dung toán điển hình gây không ít khó khăn cho các em, đòi hỏi các em cần có tư duy tốt, Toán hình cũng là bài quan trọng và chiếm nhiều điểm nhất trong các đề thi và đề kiểm tra. Để giúp các em học sinh ôn tập một cách tổng quan và dễ dàng nắm rõ hơn về cách giải của các bài toán nội dung này, chúng ta cùng tìm hiểu kĩ hơn qua một số bài toàn có nội dung hình học từ cơ bản đến nâng cao kèm lời giải chi tiết dưới đây.
Bài 1:
a: Một thửa ruộng hình chữ nhật có chu vi 100m. Người ta tăng chiều dài lên \(\dfrac{1}{3}\) chiều dài thì chu vi hình chữ nhật mới là 120m. Tính diện tích thửa ruộng ban đầu.
b: Một thửa ruộng hình chữ nhật có chu vi 100m. Người ta giảm chiều dài đi \(\dfrac{1}{3}\) chiều dài thì chu vi hình chữ nhật mới là 80m. Tính diện tích thửa ruộng ban đầu.
Giải:
a)
Nửa chu vi cũ của thửa ruộng là:
100 : 2 = 50 (m)
Nửa chu vi mới của thửa ruộng là:
120 : 2 = 60 (m)
Ta có sơ đồ như sau:
Chiều dài cũ: |----------|----------|
Chiều dài mới: |----------|----------|-----10-----|
Theo sơ đồ ta tính được:
Chiều dài ban đầu của thửa ruộng là:
10 : \(\dfrac{1}{3}\) = 30 (m)
Chiều rộng ban đầu của thửa ruộng là:
50 - 30 = 20 (m)
Diện tích thửa ruộng ban đầu là:
30 x 20 = 600 (\({{m^2}}\))
Nửa chu vi cũ của thửa ruộng là:
100 : 2 = 50 (m)
Nửa chu vi mớ của thửa ruộng là:
80 : 2 = 40 (m)
Ta có sơ đồ như sau:
Chiều dài cũ:
|----------|----------|-----10-----|
Chiều dài mới:
|----------|----------|
Chiều dài ban đầu của thửa ruộng là:
10 : \(\dfrac{1}{3}\) = 30 (m)
Chiều rộng ban đầu của thửa ruộng là:
50 - 30 = 20 (m)
Diện tích thửa ruộng ban đầu là:
30 x 20 = 600 (\({{m^2}}\))
Đáp số: 600 (\({{m^2}}\))
Bài 2:
a: Một thửa ruộng hình chữ nhật có chu vi 110m. Nếu tăng chiều rộng 5 m và giảm chiều dài 5 m thì diện tích thửa ruộng không thay đổi. Tính diện tích thửa ruộng
Giải:
Ta tính nửa chu vi hình chữ nhật:
110 : 2 = 55 (m)
Do chiều dài, chiều rộng tăng giảm 5m thì diện tích không thay đổi nên ta biết được chiều dài và chiều rộng của thửa đất hơn kém nhau 5 m
Ta tính được chiều dài thửa đất:
(55 + 5) : 2 = 30 (m)
Chiều rộng thửa đất là:
30 – 5 = 25 (m)
Diện tích thửa đất là:
30 x 25 = 750 (\({{m^2}}\))
Đáp số: 750 \({{m^2}}\)
b: Một thửa đất hình vuông trên thửa đất đó người ta đào một cái ao hình vuông cạnh cái ao cách đều cạnh thửa đất. Chu vi cái ao kém chu vi thửa đất là 64 m. Tính diện tích cái ao biết diện tích phần dất còn lại là 600\({{m^2}}\).
Giải:
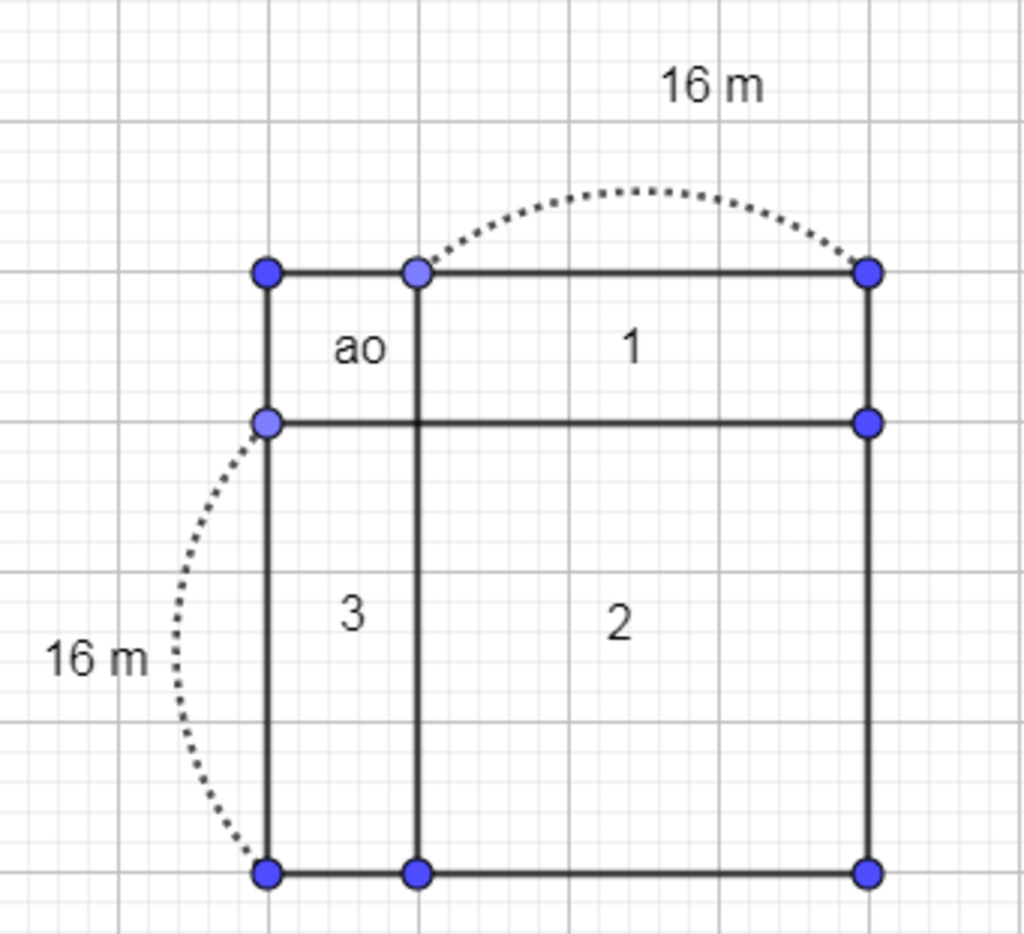
Độ dài cạnh của cái ao kém độ dài cạnh của thửa đất là:
64 : 4 = 16 (m)
Theo hình vẽ, ta có diện tích phần dất còn lại là tổng diện tích hình 1, 2 và 3.
Diện tích hình 2 là:
16 × 16 = 256 (\({{m^2}}\))
Diện tích hình 1 bằng diện tích hình 3 và bằng:
(600 − 256) : 2 = 172 (\({{m^2}}\))
Cạnh của ao là:
172 : 16 = 10,75 (m)
Diện tích ao là:
10,75 × 10,75 = 115,5625 (\({{m^2}}\))
Đáp số: 115,5625 \({{m^2}}\)
c: Bác An có một mảnh đất vườn chữ nhật .ở một góc vườn bác đào một cái ao hình vuông có 1 cạnh cách chiều rộng mảnh vườn 33 m còn cạnh kia cách chiều dài mảnh vườn là 17 m. Biết diện tích phần đất còn lại là 1311\({{m^2}}\). Tính diện tích mảnh vườn.
Giải:
Diện tích đất còn thừa (được chia làm phần đất có cạnh của cái ao) là:
1311 – 33 x 17 = 750 (\({{m^2}}\))
Cạnh của ao cá là:
750 : (33+17) = 15 (m)
Chiều dài mảnh vườn là:
33 + 15 = 48 (m)
Chiều rộng mảnh vườn là:
17 + 15 = 32 (m)
Diện tích mảnh vườn là:
48 x 32 = 1536 (\({{m^2}}\))
Đáp số: 1536 \({{m^2}}\)
d: Một thửa ruộng hình chữ nhật có chu vi 200 m .chiều dài hình chữ nhật hơn 2 lần chiều rộng là 10m.Tính diện tích thửa ruộng.
Giải:
Nửa chu vi thửa ruộng là:
200 : 2 = 100 (m)
Chiều rộng thửa ruộng là:
(100 - 10) : 3 = 30 (m)
Chiều dài thửa ruộng là:
100 - 30 = 70 (m)
Diện tích thửa ruộng là:
30 x 70 = 2100 (\({{m^2}}\))
Đáp số: 2100 \({{m^2}}\)
đ: Một thửa ruộng hình chữ nhật có chu vi 160 m .chiều dài hình chữ nhật kém 2 lần chiều rộng là 10m.Tính diện tích thửa ruộng.
Giải:
Nửa chu vi thửa ruộng là:
160 : 2 = 80 (m)
Chiều rộng thửa ruộng là:
(80 − 10) : 2 = 35 (m)
Chiều dài thửa ruộng là :
80 – 35 = 45 (m)
Diện tích thửa ruộng là:
45 × 35 = 1575 (\({{m^2}}\))
Đáp số: 1575 \({{m^2}}\)
e: Một thửa ruộng hình chữ nhật có chu vi 200 m dọc theo chiều dài người ta ngăn thửa ruộng thành 2 thửa ruộng nhỏ. Biết 1 trong 2 thửa ruộng là hình vuông và chu vi thửa ruộng hình vuông nhỏ hơn chu vi thửa ruộng hình chữ nhật nhỏ là 20m. Tính diện tích thửa ruộng ban đầu.
Giải:
Ta có hình vẽ:
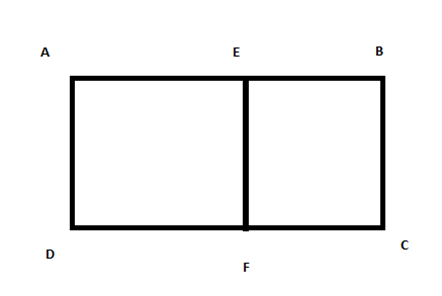
Ta vẽ hình minh họa, theo hình vẽ ta có:
Ta có nửa chu vi HCN lớn: AB + BC = 200 : 2 = 100 (m)
Suy ra AB = 100 - BC
Vì chu vi thửa ruộng hình vuông nhỏ hơn chu vi thửa ruộng hình chữ nhật nhỏ là 20m
Nên ta có:
(AE + EF) x 2 – EF x 4 = 20
Mà EF = EB = BC nên ta có
(AE + EB) x 2 – BC x 4 = 20
AB x 2 – BC x 4 = 20
(100 – BC) x 2 – BC x 4 = 20
200 – BC x 2 – BC x 4 = 20
BC x 6 = 200 – 20
BC = 180 : 6 = 30 (m)
Ta suy ra tiếp:
AB = 100 – 30 = 70 (m)
Diện tích của thửa ruộng chữ nhật ABCD là:
70 x 30 = 2100 (\({{m^2}} \))
Đáp số: 2100 \({{m^2}} \)
g: Một thửa ruộng hình chữ nhật có chu vi 160 m dọc theo chiều dài người ta ngăn thửa ruộng thành 2 thửa ruộng nhỏ. Biết 1 trong 2 thửa ruộng là hình vuông và chu vi thửa ruộng hình vuông lớn hơn chu vi thửa ruộng hình chữ nhật nhỏ là 20m. Tính diện tích thửa ruộng ban đầu.
Giải:
Tương tự câu e
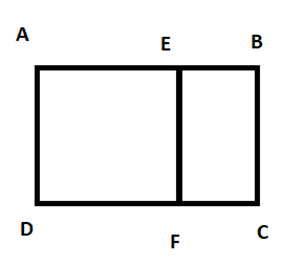
Ta có nửa chu vi HCN lớn: AB + BC = 160 : 2 = 80 (m)
Suy ra AB = 80 - BC
Vì chu vi thửa ruộng hình vuông lớn hơn chu vi thửa ruộng hình chữ nhật nhỏ là 20m
Nên ta có:
AD x 4 - (EB + BC) x 2 = 20
Mà AD = AE = BC nên ta có
BC x 4 - (EB + AE) x 2 = 20
BC x 4 - AB x 2 = 20
BC x 4 - (80 – BC) x 2 = 20
BC x 4 + BC x 2 = 160 + 20
BC x 6 = 180
BC = 180 : 6 = 30 (m)
Ta suy ra tiếp
AB = 100 – 30 = 70 (m)
Diện tích của thửa ruộng chữ nhật ABCD là:
70 x 30 = 2100 (\({{m^2}} \))
Đáp số: 2100 \({{m^2}} \)
h: Một thửa ruộng hình chữ nhật có chiều dài gấp 3 lần chiều rộng. Nếu tăng chiều rộng 5m và giảm chiều dài 5 m thì diện tích tăng thêm 300\({{m^2}}\). Tính diện tích thửa ruộng ban đầu.
Giải:
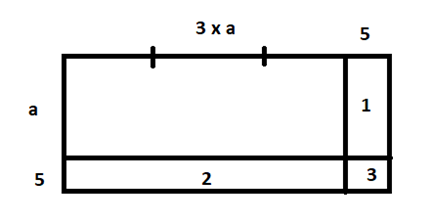
Từ hình vẽ ta thấy phần diện tích tăng lên bằng tổng diện tích của 3 hình 1, 2 và 3.
Gọi chiều rộng là a thì chiều dài là 3 x a và ta có:
Diện tích hình chữ nhật 1 là:
5 x a
Diện tích hình chữ nhật 2 là:
5 x 3 x a = 15 x a
Diện tích hình vuông 3 là:
5 x 5 = 25
Vậy 5 x a + 15 x a + 25 = 300
20 x a = 275
a = 13,75
Suy ra chiều rộng hcn ban đầu là 13,75 cm, chiều dài là 13,75 x 3 = 41,25 m.
Vậy diện tích hình chữ nhật ban đầu là:
41,25 x 13,75 = 567,1875 \({{m^2}}\)
Đáp số: 567,1875 \({{m^2}}\)
HỆ THỐNG CHƯƠNG TRÌNH HỌC CỦA MATHX
Bài 3: Một hình chữ nhật, nếu tăng chiều rộng để bằng chiều dài của nó thì diện tích tăng thêm 20\({{m^2}}\), còn khi giảm chiều dài cho bằng chiều rộng thì diện tích giảm 16 \({{m^2}}\). Tính diện tích hình chữ nhật
Giải:
Hiệu của Diện tích tăng lên và Diện tích giảm đi là:
20 – 16 = 4 (\({{m^2}}\))
Cạnh của hình vuông có diện tích 4 \({{m^2}}\) là:
4 : 2 = 2 (m)
Diện tích tăng thêm 20m2 thì chiều dài HCN là:
20 : 2 = 10 (m)
Diện tích giảm đi 16m2 thì chiều rộng HCN là:
16 : 2 = 8 (m)
Diện tích HCN ban đầu là:
10 X 8 = 80 (\({{m^2}}\))
Thử lại:
10 x (8+2) = 100 \({{m^2}}\) ; 100 - 20 = 80 \({{m^2}}\)
8 x (10-2) = 64 \({{m^2}}\) ; 64 + 16 = 80 \({{m^2}}\)
Đáp số: 80 \({{m^2}}\)
Bài 4: Một hình chữ nhật có diện tích 135\({{m^2}}\). Chiều dài bằng \(\dfrac{3}{5}\) chiều rộng .Tính chu vi hình chữ nhật.
Giải:
Chia diện tích hình chữ nhật thành:
3 x 5 = 15 (hình vuông bằng nhau)
Cạnh mỗi hình vuông = \(\dfrac{1}{3}\) chiều rộng và = \(\dfrac{1}{5}\) chiều dài
Diện tích 1 hình vuông là:
135 : 15 = 9 (\({{m^2}}\))
Ta có:
3 x 3 = 9
Vậy cạnh hình vuông = 3m
Chiều rộng hình chữ nhật là:
3 x 3 = 9 (m)
Chiều dài hình chữ nhật là:
3 x 5 = 15 (m)
Chu vi hình chữ nhật là:
(15 + 9) x 2 = 48 (m)
Đáp số: 48m
Bài 5: Một cái sân hình chũ nhật có chu vi 110 m. Người ta tăng chiều rộng lên 5m thì sân trở thành hình vuông. Tính diện tích cái sân ban đầu.
Giải:
Theo đề bài, ta có hiệu giữa chiều dài và chiều rộng sẽ là 5.
Một nửa chu vi cái sân là:
110 : 2 = 55 (m)
Chiều rộng cái sân là:
(55 - 5) : 2 = 25 (m)
Chiều dài cái sân là:
55 - 25 = 30 (m)
Diện tích cái sân ban đầu là:
30 × 25 = 750 (\({{m^2}}\))
Đáp số: 750\({{m^2}}\)
Bài 6: Một mảnh vườn hình chữ nhật có chu vi 180 m nếu giảm chiều dài 10 m thì mảnh vườn trở thành mảnh vườn hình vuông. Tính diện tích mảnh vườn ban đầu.
Giải:
Nửa chu vi mảnh vườn là:
180 : 2 = 90 (m)
Nếu giảm 10m ở chiều dài thì mảnh vườn thành hình vuông
=> Hiệu của chiều dài và rộng là 10m
Chiều dài mảnh vườn là:
(90 + 10) : 2 = 50 (m)
Chiều rộng mảnh vườn là:
90 - 50 = 40 (m)
Diện tích mảnh vườn là:
50 x 40 = 2000 (\({{m^2}}\))
Đáp số: 2000 (\({{m^2}}\))
Bài 7: Một mảnh vườn hình chữ nhật có chu vi 150 m .Nếu giảm chiều dài 10m và tăng chiều rộng 5m thì được một hình chữ nhật mới có chiều dài gấp 4 chiều rộng .Tính diện tích mảnh vườn.
Giải:
Nửa chu vi hình chữ nhật là:
150 : 2 = 75 (m)
Nửa chu vi hình chữ nhật sau khi giảm chiều dài 10m và tăng chiều rộng 5 m là:
75 - 10 + 5 = 70 (m)
Tổng số phần bằng nhau là:
4 + 1 = 5 ( phần )
Chiều dài hình chữ nhật sau khi giảm là:
70 : 5 x 4 = 56 (m)
Chiều rộng hình chữ nhật sau khi tăng là:
70 - 56 = 14 (m)
Chiều dài hình chữ nhật lúc đầu là:
56 + 10 = 66 (m)
Chiều rộng hình chữ nhật lúc đầu là:
14 - 5 = 9 (m)
Diện tích hình chữ nhật là:
66 x 9 = 594 (m2)
Đáp số: 594 m2
Bài 8: Một hình chữ nhật có chiều dài gấp 3 chiều rộng . Nếu tăng chiều rộng lên 24 m thì được hình chữ nhật mới có chiều dài gấp 3 chiều rộng. Tính diện tích hình chữ nhật.
Giải:
Ta có khi tăng chiều rộng lên 24 m thì được hình chữ nhật mới.
Vậy chiều rộng cũ khi thêm 24 m sẽ trở thành chiều dài của hình chữ nhật mới còn chiều dài cũ trở thành chiều rộng của hình chữ nhật mới.
Khi tăng chiều rộng lên 24 m thì chiều rộng trở thành chiều dài của hình chữ nhật mới và gấp 3 lần chiều dài cũ.
Nếu coi chiều rộng cũ là 1 phần thì chiều dài cũ là:
1 × 3 = 3 (phần)
Chiều dài mới hay chiều rộng cũ khi tăng 24 m có số phần là:
3 × 3 = 9 (phần)
24 mét ứng với số phần là:
9 − 1 = 8 (phần)
Chiều rộng ban đầu là:
24 : 8 × 1 = 3 (m)
Chiều dài ban đầu là:
3 × 3 = 9 (m)
Diện tích hình chữ nhật là:
9 × 3 = 27 (m2)
Đáp số: 27 m2
* Giải thích cách làm:
Vì khi tăng chiều rộng lên 24 m được hình chữ nhật mới thì chiều rộng cũ khi thêm 24 m sẽ trở thành chiều dài của hình chữ nhật mới còn chiều dài cũ trở thành chiều rộng của hình chữ nhật mới
Khi tăng chiều rộng lên 24 m thì chiều rộng trở thành chiều dài của hình chữ nhật mới và gấp 3 lần chiều dài cũ.
Nếu coi chiều rộng cũ là 1 phần mà chiều dài cũ ấp 3 chiều rộng cũ nên chiều dài cũ có số phần là:
1 × 3 = 3 (phần)
Vì chiều rộng cũ khi thêm 24 m sẽ trở thành chiều dài của hình chữ nhật mới còn chiều dài cũ trở thành chiều rộng của hình chữ nhật mới và chiều dài mới gấp 3 chiều rộng mới nên chiều dài mới hay chiều rộng cũ khi tăng 24 m có số phần là:
3 × 3 = 9 (phần)
Chiều rộng thêm 24 m = Chiều rộng cũ + 24 m
Số phần 24 m = Số phần của chiều rộng thêm 24 m - Số phần chiều rộng cũ
Diện tích hình chữ nhật = Chiều dài × Chiều rộng
Bài 9: Một mảnh vườn hình chữ nhật có chiều dài gấp 4 lần chiều rộng . Nếu tăng chiều dài 5m và giảm chiều rộng 5 m thì diện tích giảm đi 256m2. Tính diện tích mảnh vườn.
Giải:
Hiệu giữa 5 lần chiều dài ban đầu với 5 lần chiều rộng ban đầu là:
250 − 25 = 225 (m2)
Ban đầu chiều dài hơn chiều rộng là:
225 : 5 = 45 (m)
Hiệu số phần bằng nhau là:
4 − 1 = 3 (phần)
Chiều rộng khu vườn là :
45 : 3 = 15 (m)
Chiều dài khu vườn là:
15 × 4 = 60 (m)
Diện tích khu vườn là:
15 × 60 = 900 (m2)
Đáp số: 900 m2
Bài 10: Sân trường em hình vuông .Để tăng thêm diện tích nhà trường đã mở rộng về mỗi phía 4m thì diện tích tăng thêm là 196 m2 . Hỏi trước đây sân trường em có diện tích là bao nhiêu m2?
Giải:
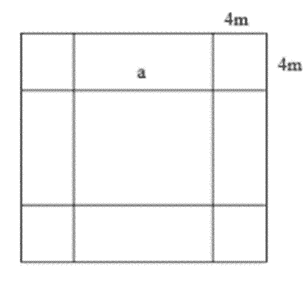
Diện tích tăng thêm bằng diện tích 4 hình vuông nhỏ cạnh bằng 4m và 4 hình chữ nhật có 1 cạnh bằng 4 m và 1 cạnh bằng cạnh hình vuông
Diện tích 4 hình vuông nhỏ là:
4 x (4 x 4) = 64 (m2)
Diện tích 4 hình chữ nhật là:
192 - 64 = 128 (m2)
Diện tích 1 hình chữ nhật là:
128 : 4 = 32 (m2)
Cạnh hình vuông đã cho là:
32 : 4 = 8 (m)
Diện tích sân trường lúc chưa mở rộng là:
8 x 8 = 64 (m2)
Đáp số: 64 m2
Trên đây MATHX đã hướng dẫn các em giải một số bài toán có nội dung hình học từ cơ bản đến nâng cao lớp 4. Hy vọng các em hiểu bài và ôn tập thật tốt để thành công trong các kì thi cuối cấp sắp tới.
Ngoài ra các em có thể tham khảo thêm các tài liệu sau để có thể ôn tập toán lớp 4 hiệu quả: TOÁN NÂNG CAO LỚP 4 - HÌNH CHỮ NHẬT, HÌNH THOI